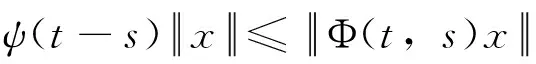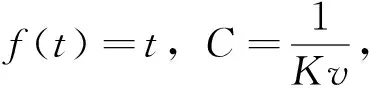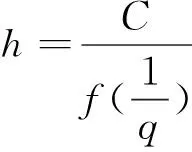Banach空间中GC(0,e)类广义发展算子的一致指数不稳定性*

岳田，宋晓秋

(1. 湖北汽车工业学院理学院，湖北 十堰 442002；2. 中国矿业大学数学学院，江苏 徐州 221116)

除了指数稳定性以外，近年来关于发展方程的指数不稳定性方面也获得了极大的关注[8-12]。 如文献[8]利用容许性方法、文献[9-10]利用赋范函数空间的方法探讨了线性斜积半流的指数不稳定性的存在条件。文献[11-12]分别给出了Banach空间中线性斜演化半流的一致指数不稳定性和非一致指数不稳定性的若干刻画。

作为传统发展算子的推广，葛照强与冯德兴在文献[13]中定义了一种新的广义发展算子，即在Banach空间X上具有性质(ii)(见定义1)，文中对其存在性、唯一性进行了相关探讨。在文献[14]中，作者讨论了广义发展算子一致指数稳定性的充要条件，所得结果在研究时变广义分布参数系统的稳定性方面将有重要的价值。值得注意的是，文献[14]中结果可以判定系统Ex′(t)=A(t)x(t)的稳定性，这样弥补了利用单参数半群或发展算子不能判定此系统稳定性的缺陷。本文的主要目的是研究GC(0,e)类广义发展算子的一致指数不稳定性。

1 预备知识

(i)f(t)>0,∀t>0；

F2表示所有满足如下性质的非减连续函数f:R+→R+构成的集合：

(i)f(t)>0,∀t>0；

定义1[14]设E∈B(X)。Φ(t,s):Δ→B(X)称为由E引导的GC(0,e)类广义发展算子，或简称GC(0,e)类广义发展算子，如果它满足如下四条性质：

(i) Φ(s,s)=Φ0,s∈[0,∞)，其中Φ0∈B(X)；

(ii) Φ(t,r)EΦ(r,s)=Φ(t,s),∀(t,r),(r,s)∈Δ；

(iii)Φ(·,s)在[s,∞)上强连续且Φ(t,·)在[0,t]上强连续；

定义2GC(0,e)类广义发展算子Φ(t,s)称为一致指数不稳定的如果存在常数K>0和v>0使得对所有t≥s≥0和x∈X，有

(1)

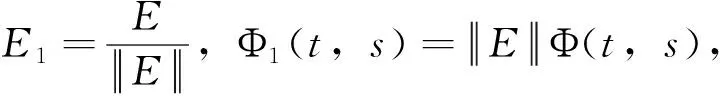
2 主要结果

定理1 设Φ(t,s)是GC(0,e)类广义发展算子，则Φ(t,s)一致指数不稳定的充要条件是存在两个常数h>0和q>1使得对每个x∈X和s≥0存在τx,s∈(0,h]满足

(2)

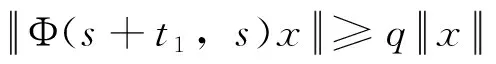
记s0=t0=0。由数学归纳法可以找到一个序列(tn)n∈N,(tn∈(0,h],n∈N+)使得

(3)

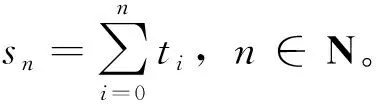
设t≥0，则存在n∈N使得sn≤t

进而

(4)

充分性。依据函数φ的性质可知存在常数δ>0使得φ(δ)<1，易知对任一(t,s)∈Δ存在n∈N和l∈[0,δ)使t-s=nδ+l。进而由已知条件可得

(5)

定理3 设Φ(t,s)是单射GC(0,e)类广义发展算子，则Φ(t,s)一致指数不稳定的充要条件是存在函数f∈F1及常数C>0使得对于任一x∈X{0}及s≥0，有

(6)

证明必要性。如果Φ(t,s)是一致指数不稳定的，则由定义存在K>0,v>0使得对于任一x∈X{0}及s≥0，有

充分性。利用反证法。如果Φ(t,s)不是一致指数不稳定的，根据定理1可得，对所有h>0及q>1存在s0≥0和x0∈X使得对所有τ∈(0,h]，有

(7)

特别地，对h=Cf(2)及q=2成立。由式(7)有

这与式(6)矛盾。因此，Φ(t,s)是一致指数不稳定的。

定理4 设Φ(t,s)是单射GC(0,e)类广义发展算子，则Φ(t,s)一致指数不稳定的充要条件是存在函数f∈F2及常数C>0使得对于任一x∈X{0}及s≥0，式(6)成立。

证明必要性。令f(t)=t即可。

这与式(6)矛盾。因此，Φ(t,s)是一致指数不稳定的。

注2 定理3与定理4针对GC(0,e)类广义发展算子，将指数稳定性理论中若干经典结论[3-4,14]推广到了一致指数不稳定性情形。

推论2 设Φ(t,s)是单射GC(0,e)类广义发展算子，则Φ(t,s)一致指数不稳定的充要条件是存在常数p>0及C>0使得对于任一x∈X{0}及s≥0，有

(8)

证明在定理3中令f(t)=tp即可。

注3 推论2针对GC(0,e)类广义发展算子，将指数稳定性理论中Datko[1]型结论推广到了一致指数不稳定性情形。

下面推论将给出定理3与定理4的离散情形。

推论3 设Φ(t,s)是单射GC(0,e)类广义发展算子，则Φ(t,s)一致指数不稳定的充要条件是存在函数f∈F1∪F2及常数C′>0使得对于任一x∈X{0}及s≥0，有

(9)

证明令f(t)=t可得必要性。

充分性。 设

若f∈F1，由式(9)，对于任一x∈X{0}及s≥0，有

如果f∈F2，对于任一x∈X{0}及s≥0，有

利用定理3和定理4可知Φ(t,s)是一致指数不稳定的。

推论4 设Φ(t,s)是单射GC(0,e)类广义发展算子，则Φ(t,s)一致指数不稳定的充要条件是存在常数C′>0使得对于任一x∈X{0}及s≥0，有

(10)

证明在推论3中令f(t)=t即可。

定理5 设Φ(t,s)是单射GC(0,e)类广义发展算子，则Φ(t,s)一致指数不稳定的充要条件是存在常数C>0和α>0使得对于任一x∈X{0}及(t,s)∈Δ，有

(11)

证明必要性。如果Φ(t,s)是一致指数不稳定的，则由定义2存在K>0,v>0使得对于任一x∈X{0}及(t,s)∈Δ，有

充分性。如果Φ(t,s)不是一致指数不稳定的，设h>0满足eαh>1+2αhC，其中C和α由式(11)给出，由定理1，对q=2存在s0≥0及x0∈X{0}使得对所有的τ∈(0,h]，式(7)成立。从而对t=s0+h，有

这与式(11)矛盾。因此，Φ(t,s)是一致指数不稳定的。