区间模糊谱聚类图像分割方法*
刘汉强,张 青
(陕西师范大学计算机科学学院,陕西 西安 710119)
1 引言
图像分割是计算机视觉领域的重要组成部分[1,2]。图像分割算法有很多种,包括基于阈值的分割方法、基于聚类的分割方法和基于区域的分割方法等。聚类分析是一种将研究对象划分为相对同质的类或者簇的统计分析方法[3]。由于无监督的特性,聚类分析已经被广泛应用于模式识别、数据挖掘、计算机视觉等很多领域[4]。基于聚类的图像分割是一种常用的图像分割方法,并已得到广泛应用。谱聚类算法[5,6]是一种更加有效的聚类算法,与传统的聚类算法相比,它能在任意形状的样本空间上聚类,且收敛于全局最优解。谱聚类是建立在谱图理论基础之上的,首先根据给定的样本数据集构造数据间的相似性矩阵,进而计算该矩阵的特征值和特征向量,然后选择合适的特征向量对不同的数据点进行聚类。经典的谱聚类算法有2000年Shi和Malik[7]提出的SM算法、2001年Zha等人[8]提出的基于二分图上的谱聚类算法以及2002年Ng等人[9]提出的k-way划分的NJW算法等。
谱聚类的优点是直接对相似性矩阵进行计算,不需要样本服从特定分布,但是传统的谱聚类算法仍存在着一些问题。首先,谱聚类算法的关键是构造相似性矩阵,传统的相似性度量采用高斯核函数,然而这个度量存在明显的缺陷,即对高斯核函数中的尺寸参数σ的选取非常敏感,该参数很难选取,并且基于欧几里得的高斯核相似性度量无法完全反映复杂数据集的空间分布特点[10]。因此,如何选取合适的相似性度量成为谱聚类算法的关键问题,也是一大挑战。很多人试图改变相似性测度模型以提高分割精度,Chapelle等人[11]以高斯核函数为基础改进相似性测度,其中采用了 Dijkstra算法求最短路径。Kim等人[12]通过引进一种半监督学习技术改进了相似性测度模型。Zhao等人[13]利用模糊C-均值聚类得到的划分矩阵提出了模糊相似性度量。以上这些算法通过改进相似性测度的方法在一定程度上改进了分割效果。另外,由于谱聚类算法属于图论的范畴,所以不可避免地会存在图论分割图像的缺点:图像分割是基于像素级别的,随着像素点的增加,计算复杂度会越来越高。为了降低时间复杂度,提高运算效率,Fowlkes等人[14]提出了采样可近似估算邻接矩阵和特征向量的Nyström算法。
由于人的视觉特性和数字图像本身所具有的模糊性,使得图像分割问题呈现出典型的结构不良问题,模糊集理论[15,16]具有描述不良问题的能力,所以将模糊理论引人图像分割中,可以获得更好的图像分割效果。模糊理论通过隶属度函数来描述样本对不同类别的隶属程度,不但描述了样本的划分特性,而且体现出了样本与各划分类之间的关联程度。目前比较经典的算法是基于目标函数的模糊C均值聚类算法FCM(FuzzyC-Means)。但是FCM在处理噪声、参数等不确定因素时结果不够理想,随后人们引入二型模糊集[17,18]概念。Hwang和Rhee[19]在对二型模糊聚类研究的基础上,用两个不同的模糊指数构造隶属度区间,提出了区间二型模糊C均值聚类IT2FCM(Interval-valued Type-2 FuzzyC-Means clustering)方法。二型模糊集的引入对FCM算法性能有了一定的提升,对模糊聚类在图像分割中的应用也将有进一步的提升。针对传统的谱聚类算法相似性测度不易构造和计算复杂度高等问题,本文提出了一种区间模糊谱聚类图像分割方法,通过引入区间模糊集,构造有效的区间模糊相似性测度,提高谱聚类的算法性能。此外,由于图像中灰度值的变化范围是有限的,仅在[0,255],因此区间模糊相似性测度是建立在图像的灰度直方图上,降低了所提方法的时间复杂度。实验结果表明,本文方法既能保证图像目标的完整性,还能体现出图像中的细节信息。
2 谱聚类理论
谱聚类的理论基础是图谱理论,将图像看成是一种基于某种相似性的无向加权图G=(V,E),其中,V代表一个样本在图中的顶点,E为连接顶点的边,w是边上的权值。图谱理论涉及到图的相似性矩阵的谱和图的Laplace矩阵的谱,因此构造邻接矩阵是非常关键的步骤。应用谱聚类进行图像分割时,一般需构造图像中像素之间的相似性矩阵,因此该相似性矩阵的存储和有效性对最终的分割结果至关重要。比较经典的谱聚类方法是Shi和Malik[7]提出的SM算法以及Ng等人[9]提出的k-way划分的NJW算法。不同准则函数的选取对应于谱聚类有着不同的实现方法,但是基本框架都是一致的,以NJW算法为例,基本步骤如下:
(1)根据样本间的某种相似性测度构造相似性矩阵W,传统谱聚类基本都是基于欧氏距离的高斯核函数来度量样本数据点之间的相似性,构造相似性矩阵W。图像像素信息为X=(x1,x2,…,xn),像素间的相似性如下所式:
(1)
其中,σ为尺度参数。
(2)构造拉普拉斯矩阵L=D-1/2WD-1/2,其中D为度矩阵,对角元素为:
(2)
(3)计算L的前k个特征值对应的特征向量vi(必要时进行正交化),构造矩阵:
V=[v1,v2,…,vk]
(3)
(4)将V的行向量转化为单位向量,得到矩阵Y。
(4)
(5)把Y中的每行当做k维空间中的点,用聚类算法进行聚类,所对应的每一行的分类就是原始数据的划分。
3 基于区间模糊相似性的谱聚类图像分割
谱聚类应用于图像分割时,相似性矩阵的存储和有效性是一个非常关键的问题。此外,如果能够更好地利用图像的灰度信息以及区间模糊的细节信息,则能够提高谱聚类的分割性能。鉴于此,本文提出一种基于区间模糊相似性的谱聚类图像分割方法。
3.1 区间模糊聚类理论知识
1975年,Zadeh教授[18]提出了二型及多型模糊集的概念。其中二型模糊集中的元素由[0,1]扩展为一型模糊集,取值范围从二维空间延伸到了三维空间,因此具有更强处理不确定性的能力。区间二型模糊集合是一类特殊的二型模糊集合,其次隶属度值都为1。相比一般二型模糊集合,区间二型模糊集合省略了次隶属度函数的选择与运算,减少了因维度增加而导致的复杂度增加,所以在实际生活中得到了更加广泛的应用。由于区间二型模糊集合的运算复杂度小,并且具有二型模糊集处理不确定性的特点。
3.2 基于灰度的区间模糊相似性测度的构造
在利用谱聚类进行图像分割时不可避免需要构造像素间的相似性测度,此时计算时间复杂度高,容易降低运算效率。一幅图像至多有256个灰度,灰度直方图是关于灰度级分布的函数,是对图像中灰度级分布的统计。因此,图像中灰度的数量总是远远小于图像的大小,本文利用图像的灰度直方图,通过统计灰度的模糊隶属度来构造基于灰度的区间模糊相似性测度。
在传统的模糊聚类算法中,由于单一的模糊加权指数m无法针对不同类型的数据集得到理想的决策边界,所以引入多个模糊加权指数的方式构造决策边界。不同的m值对隶属度函数的影响不同,同时也会影响图像分割的结果。Hwang等人[19]提出通过两个参数m1和m2来构造区间二型模糊集的主隶属度函数,而次隶属度函数则通过设置所有次隶属度值为1进行构造。假设图像的灰度l属于[0,255],该灰度在图像中出现的频率用γl来表示,图像灰度的区间二型模糊集的上、下模糊隶属度可以通过不同的m1和m2来得到,将灰度l张成与聚类中心vk同维度的灰度向量l。下面首先介绍m1和m2对应的基于灰度的模糊目标函数:
(5)
(6)
通过对模糊C均值目标函数的优化方法,可以得到与两个模糊指数对应的隶属度更新公式,依据此更新公式,我们构造了基于灰度的上下模糊隶属度函数,即:
(7)
(8)

(9)
最终,降型后的模糊隶属度为:
(10)
利用式(10)得到隶属度矩阵uil,可以构造基于灰度的区间模糊相似性测度:
Sll′=max({min(uil,uil′)}i=1,2,…,C)
(11)
3.3 基于区间模糊相似性测度的谱聚类图像分割
根据构造的基于区间模糊相似性测度,可以构造图像灰度值之间的带权无向图,因此可以采用规范切准则对该图进行划分。由于规范切准则的谱放松解位于拉普拉斯矩阵(L=D-1/2SD-1/2,D为度矩阵)的前k个最大特征值对应的特征向量张成的子空间上,这样做将原问题转换为求解矩阵的特征值和特征向量的问题。
通过本节对相关技术的分析,本文算法步骤如下:
输入:待分割的图像I,聚类数目C,模糊系数m=2,初始化中心,参数m1和m2。
输出:图像的分割结果。
步骤1读入图像I,计算灰度直方图,直方图中用γl表示出每个灰度出现的频率。
步骤2利用参数m1和m2计算上下隶属度,并通过KM降型算法[20]迭代计算聚类中心的区间值[vL,vR]和模糊隶属度的区间值[μL,μR],并最终得到降型后的区间模糊隶属度和聚类中心。
步骤3利用式(11)得到相似性矩阵S并构造拉普拉斯矩阵L。

步骤5将F的每一行看成是Rk空间中的一个点,使用k均值聚类算法或其它聚类算法将其聚为C类,所对应的每一行的分类就是原始数据的划分。
步骤6根据上一步的划分结果得到输入图像最终的分割结果。
4 实验分析
为了验证本文提出的区间模糊谱聚类图像分割方法的正确性和有效性,选取了Berkeley图像库中的5幅图像(#8068,#2009_005130,#163014,#118035,#24063) 进行对比实验。对比方法包括本文方法、FCM算法、Nyström算法。Nyström算法的欧氏距离中的参数σ影响了实验的稳定性。本文方法中不同的参数(m1,m2)对分割结果的影响不同,所以在实验中选取了四组不同的参数值([1.5,2],[2,3],[3,5],[5,5])来进行对比。
从图1~图5的分割结果可以看出,FCM算法和Nyström谱聚类算法获得的分割结果错分比较多,并且Nyström算法在不同的参数σ下的分割效果差异较大,导致其稳定性不好,影响了分割结果。特别是#8068图使用Nyström谱聚类算法分割得到的结果背景错分严重,FCM算法没有分出目标倒影在水中的细节,而本文方法的第三小组(参数m1,m2取值[3,5])将细节处理得很好;#118035图使用Nyström谱聚类算法分割得到的屋顶十字架有错分;#24063图使用FCM算法分割得到的背景右上角有明显的错分,而本文方法的第三小组(参数m1,m2取值[3,5])背景分割明确,没有出现错分。本文方法由于引入了区间模糊隶属度构造相似性测度,更好地处理了图像细节的划分,从分割结果的整体性和准确性上都获得了比较理想的效果。表1中展示了5幅图像使用FCM算法、Nyström算法以及本文方法(参数m1,m2取值[3,5])所用时间对比。
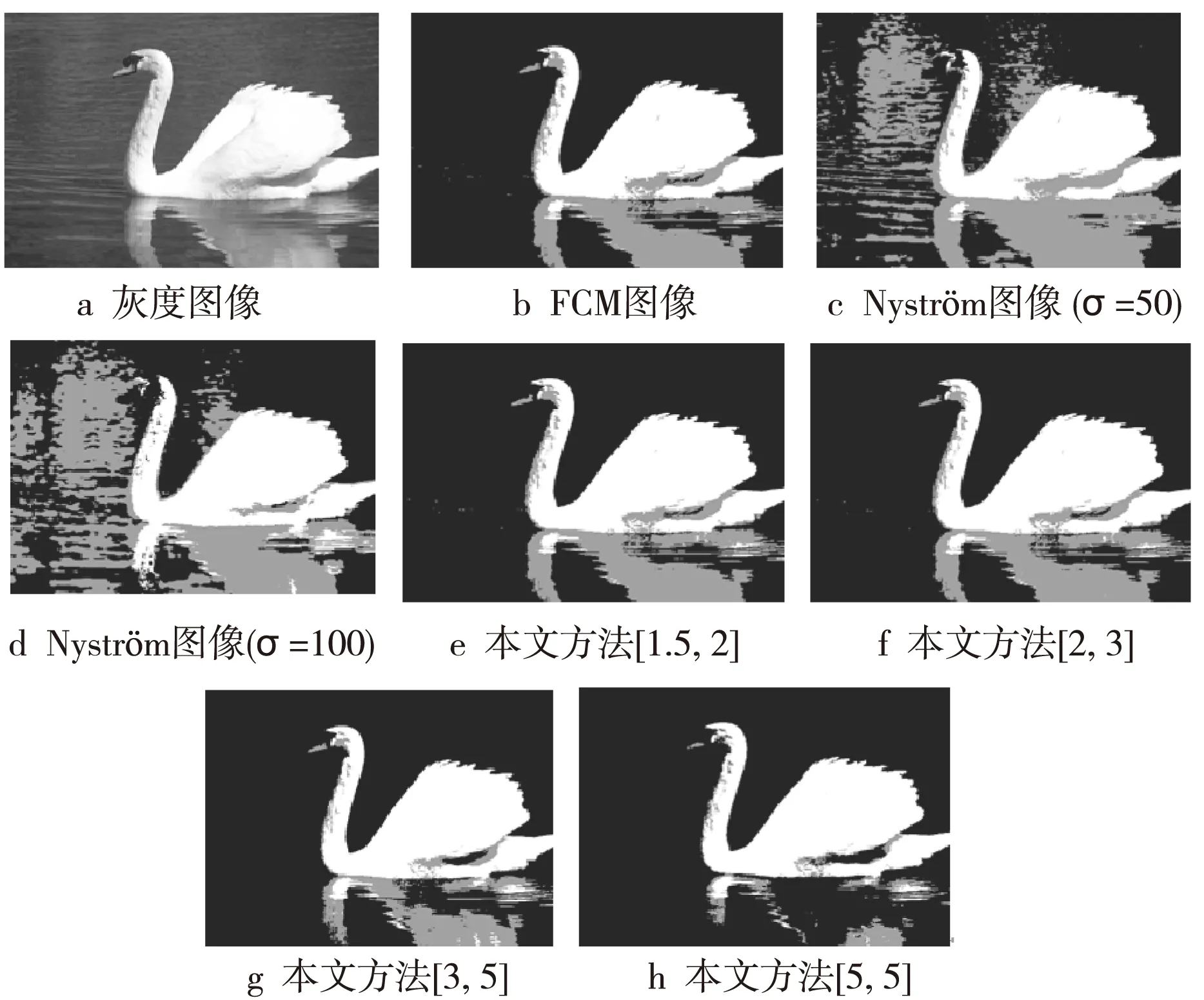
Figure 1 Comparison of segmentation results on #8068(three clusters)图1 各算法分割#8068图像结果对比图(分3类)

Figure 2 Comparison of segmentation results on #2009_005130(three clusters)图2 各算法分割#2009_005130图像结果对比图(分3类)
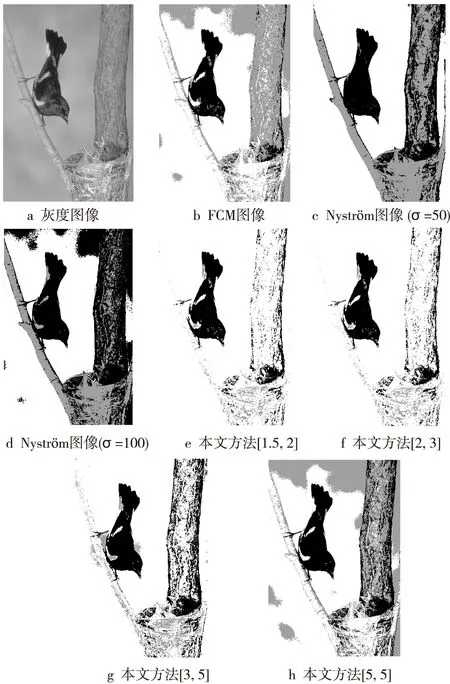
Figure 3 Comparison of segmentation results on #163014(three clusters)图3 各算法分割#163014图像结果对比图(分3类)

Figure 4 Comparison of segmentation results on #118035(three clusters)图4 各算法分割#118035图像结果对比图(分3类)

Figure 5 Comparison of segmentation results on #24063(three clusters) 图5 各算法分割#24063图像结果对比图(分3类)

通过以上各算法的时间对比可以看出,本文方法要明显优于谱聚类中的Nyström算法,由于Nyström算法本身就是为了提高谱聚类算法的运算速度而提出来的优化算法,所以本文方法在运算速度方面要优于传统的聚类算法。
5 结束语
本文提出了一种区间模糊谱聚类图像分割方法。首先将输入的彩色图像转换成灰度图像,然后利用区间模糊理论获得直方图的区间模糊隶属度,进而构造相似性测度,最后利用该测度构造的拉普拉斯矩阵的特征向量进行聚类并获得最终的分割结果。实验结果表明,本文方法加快了图像分割的速度并提高了算法的效率,获得了比较理想的分割结果。此外,如何快速构造相似性测度来纠正一些传统算法对图像的错分现象,仍然是下一步研究的重点。

