CRSHE：基于同态加密的新型密文检索方案*

付 伟，李墨泚，赵华容，吴 勇

(1.海军工程大学信息安全系,湖北 武汉 430033;2.海军密码管理中心,北京 100841)

1 引言

云存储(Cloud Storage)[1]是在云计算(Cloud Computing)[2]概念上延伸和发展出来的一种新兴网络存储技术。它采用网格技术、分布式文件系统、集群应用、虚拟化等功能，用软件来控制网络中大规模异构存储设备，并向远程用户提供按需服务的海量数据存储、访问和处理功能[3]。云存储大大节约了存储硬件和软件开销，减少了维护人员投入，具有低成本、高利用率等突出优点。同时，专业的云存储服务提供商具有普通用户无法比拟的技术和管理水平，可以为用户提供更好的冗余备份、灾难恢复等数据安全服务。

为了防止隐私泄露，用户通常选择将数据加密后再上传至云存储平台，由自己保管解密密钥，例如政府文件、全民医疗健康数据、企业商业机密相关文件、个人隐私数据等。然而，经过加密处理后的数据会失去原始明文所具有的一些特性，如有序性、相似性等，导致传统基于明文的检索方案在加密云存储系统中无法正常工作。为此，研究人员提出基于密文的安全检索问题。技术思想主要分为两类：第一类是基于索引文件的检索方法[4 - 6]，第二类是基于匹配的检索方法[7 - 10]。然而，这两种方法或者需要维护复杂的索引结构，或者检索效率较低，难以满足云存储环境下对海量密文数据的检索需要。

同态加密是一种可以直接对密文数据进行处理的加密方法[11 - 14]，可以在有效保护用户敏感数据隐私性的前提下直接对密文实施加法和乘法等同态操作，并在操作的同时保持该密文对应的明文顺序。但是，同态加密方案需要极大的计算开销。如何设计运算开销较小、方便索引的同态密文检索方案是当前研究的难点。

本文针对云存储数据管理需求提出一种面向密文存储与检索的云存储模型，并在基于整数的同态加密方案基础上设计了一种新型加密方案，提出一种新型基于同态加密的密文检索CRSHE(Ciphertext Retrieval Scheme based on Homomorphic Encryption)。

2 国内外研究现状

随着云存储应用领域的不断拓展，针对密文数据检索的研究成为当前研究的热点之一。目前，针对加密数据的检索技术主要分为两类：

第一类是基于索引文件的检索方法，即为关键词建立安全索引，通过检索索引查询关键词是否存在，判断加密数据中是否包含检索关键词。Boneh等[4]基于双线性映射提出一种可检索的公钥加密方案SPKE(Searchable Public Key Encryption)，但每次检索时服务器都需要对加密数据文件进行线性扫描，以获得检索结果，查询效率较低。Goh[5]提出使用Bloom filters构造文件的索引，但存在一定的错判率。为了获取更高效的搜索性能，Chang等[6]为整个文件集合建立一个单一的加密Hash表索引，但是这种基于词频的方案查询会大大增加服务器端的开销。

第二类是基于匹配的检索方法，即通过逐一扫描加密后的数据文件，从中寻找与检索关键词匹配的单词，从而定位出所需要的文件。Song等[7]提出了一种可检索的序列加密方法，其线性搜索方案实质上是一次一密的加密信息检索算法，抗统计分析的能力不足，且逐次匹配密文信息使得这种检索方法在大数据集、特别是多关键词查询时计算量巨大。Goh[5]提出一种基于安全索引的检索方案，但其索引结构构建和维护开销较大。此外，Lin 等[8]提出一种基于通配符(Wildcard-based)的云端加密数据的模糊关键词检索技术，部分解决了模糊密文检索问题，但是需要语义库的支持。Boneh等[9]提出一种基于公钥加密的关键词查找方案PEKS(Public-key Encryption with Keywork Search)，但是该方案需要将查询对象和查询关键词逐个比对，不适合于数据量大、检索范围不确定的加密文本检索。

此外，研究人员还提出基于可搜索加密的检索方法，即通过设计特殊的加密机制，利用陷门信息对密文直接执行搜索操作。1978年，Rivest等[10]首次提出同态加密的概念，但是直到2009年才由IBM的Gentry从数学上提出了全同态加密的可行方法[11]。随后他又和他人合作提出了两个整数上的全同态加密方案DGHV[12]和CAFED[13]。然而这三种方案的效率非常低下，都需要增加上万亿倍的运算量。Byun等[14]提出一种基于双线性对的检索方案，需要对每个文件计算双线性对，并不适合大量文件的云应用环境。Cash等[15]提出一种同时支持布尔查询和海量数据的方案，但该方案不能保证陷门的不可关联性。Chang等[16]在可搜索对称加密的安全定义基础上给出了一种基于模拟的安全性定义，但该定义不能抵御敌手进行适应性询问后的攻击。

在国内，蔡克等[17]提出了一种基于单断言的安全密文区间检索方案。该方案提供了一种唯密文条件下的区间密文检索方法，安全性较好、效率较高。但是，其密文区间检索方案限于唯密文的场景，对于服务器了解敏感数据相关背景或服务器了解部分索引与敏感数据的对应关系等场景均未涉及。宋伟等[18]基于B+树构建了一种安全密文全文索引结构，并在此基础上提出一种基于密文的全文检索方案Mimir，可以有效地抵御已知明文攻击、选择明文攻击和词频统计攻击。Li等[19]提出一种改进的基于整数同态加密的密文检索方案，可实现单关键字的密文检索。该方案对基于整数的同态加密算法进行了简化，服务器能够以较小代价破解获得密钥，故安全性有待加强。

传统密文检索技术虽然能够初步满足查全率和查准率的需求，但是检索效率普遍不高，也不能满足多关键词查询和结果排序等要求。与上述方案相比，本文提出的基于全同态加密的密文检索机制基于同态加密机制，并添加伪随机噪声，可以有效地抵御已知明文攻击、选择明文攻击和词频统计攻击，能够保护使用者的数据隐私和检索关键字安全，并能够在多关键词检索时提升检索效率，具有一定的应用前景。

3 CRSHE机制设计

CRSHE机制包括加密方案CRSHE_Enc、解密方案CRSHE_Dec、单关键字检索方案CRSHE_Rtr和多关键词检索方案CRSHE_RMK4个部分。

3.1 模型与符号定义

通常情况下，云存储服务提供方会忠实履行服务承诺，为用户提供有质量保障的存储服务；它不会对用户上传的密文数据实施唯密文攻击破译或者故意实施篡改、删除等攻击行为。然而，它却会有意收集用户的访问行为、操作记录、敏感信息等数据。

针对密文存储与检索需求，本文提出一种支持检索与共享访问功能分离的云存储系统模型。该模型包括云存储系统、数据拥有者、数据检索者和数据共享者4个角色，如图1所示。

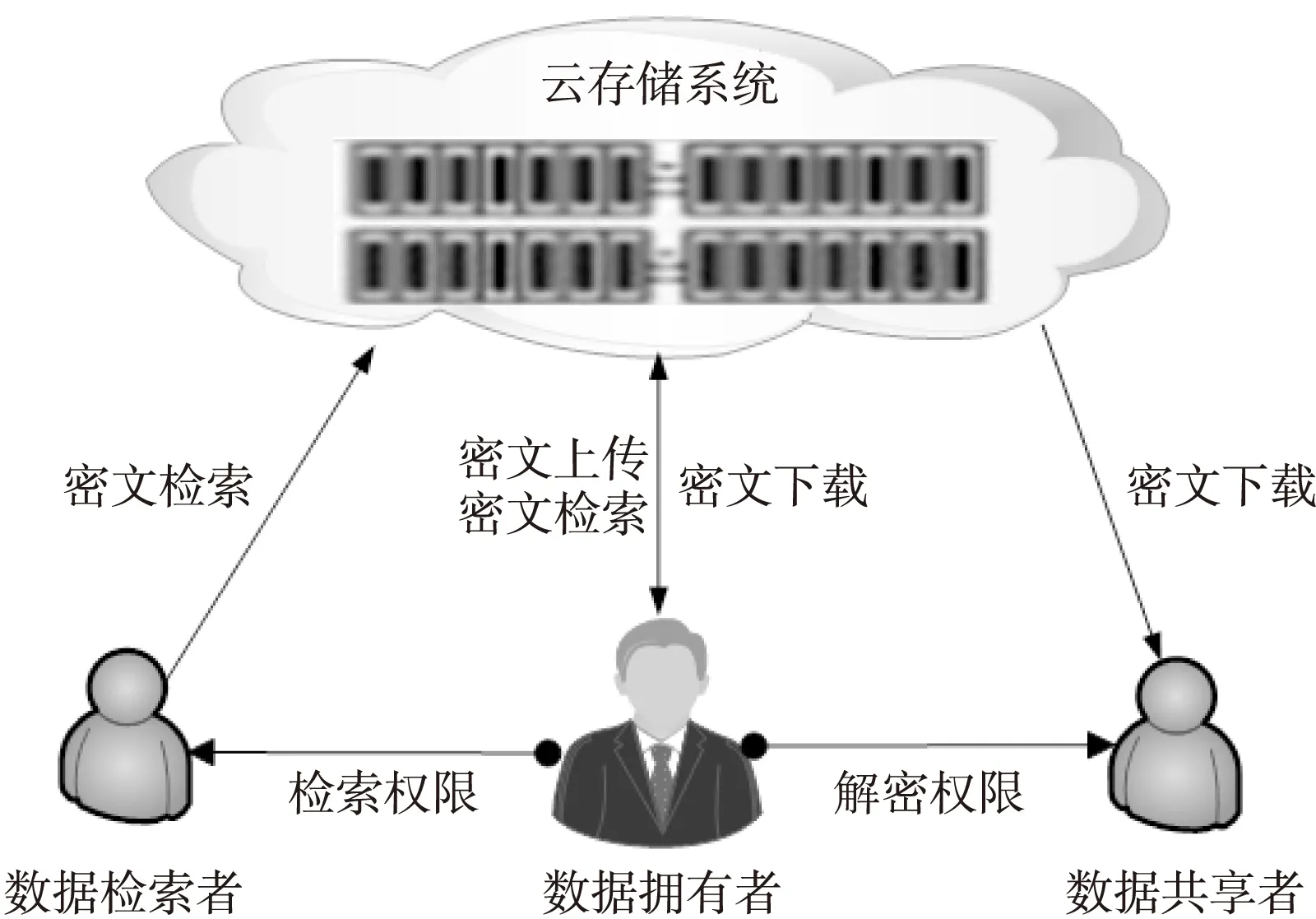
Figure 1 A cloud storage model for encrypted data retrieval and sharing图1 面向密文检索与共享的云存储模型

图1中，云存储系统为大量用户管理海量的密文数据文件；数据拥有者将自己的数据加密后上传至云存储系统，他可以自己检索或者下载数据，也可以将检索权限和密文共享权限分别指派给自己的合作者，包括数据检索者和数据共享者；数据检索者只能通过关键词在云存储中检索感兴趣的密文，但是不能获得明文；而数据共享者则只能对获得的密文进行解密，但无法执行搜索操作。与现有其它模型相比，该模型实现了搜索和解密功能的分离，更有利于保护用户的隐私数据。本文所使用的符号定义如表1所示。

Table 1 Symbol definition表1 本文所用符号定义表

3.2 基本函数

(1)密钥生成函数：GenKey(π)→P，Q，g，x。

令π为系统参数集合，该函数随机生成两个安全大素数P、Q作为密钥(Q>P)；然后寻找ZP的生成元g，并选择秘密数x使得gx为有限半群〈ZP,*〉的一个幂等元。

(2)伪随机函数：ψκ(π)→R。

令κ为用户保管的、数据m对应的密钥，在每次使用加密函数Encrypt之前，该函数生成一个长度为|R|位的伪随机整数R。

(3)加密函数：Encrypt(m)→c。

给定安全大素数P、Q和随机数R,m是长度为l的明文分组所对应的整数，据式(1)计算：

c=mgx+RP+RPQ

(1)

可得到m对应的密文c(注意Q≥P>m)。

(4)解密函数：Decrypt(c)→m。

给定安全大素数P和密文c,据式(2)计算:

m=cg-xmodP

(2)

可得到c对应的明文m。

3.3 数据加密方案CRSHE_Enc

(1)系统参数生成。使用GenKey()函数生成与m对应的大素数P、Q及秘密数x、g，使用函数ψκ(π)生成用于检索的伪随机整数R。

(2)明文分组。用户首先将明文进行分组，分组长度为l，即：M=m1m2…mr，r=|M|/l。

(3)分组加密。分别对每个明文分组mi实施Encrypt()运算，得到对应的密文分组ci=migx+RP+RPQ，1≤i≤r。

(4)密文上传。先将密文分组拼接起来形成完整密文C=c1c2…cr，然后将文件C和安全大素数Q一起发送给服务器保存。

3.4 密文解密方案CRSHE_Dec

(1)密文下载。用户向云存储服务器请求下载密文文件C；用户收到C后，对密文消息进行分组，得到C=c1c2…cr。

(2)密文分组解密。针对每个密文分组ci，使用安全大素数P和解密算法Decrypt()获得解密结果mi。

(3)明文重组。将所有明文分组按照分组顺序拼接，得到原始明文M=m1m2…mr。

3.5 单关键字密文检索方案CRSHE_Rtr

(1)检索请求生成。针对安全大素数P和检索关键词k，用户计算检索关键词对应的密文K= (kgx+RP+RPQ)modQ=(kgx+RP)modQ，然后将K作为搜索请求上传至云存储服务器。

(2)密文检索过程。云存储服务器从加密文件C中依次读取密文分组ci(1≤i≤r)，计算密文分组累乘积И=Πci，并计算И/KmodK。若结果为0，则表示关键词检索命中，检索计数器count加1；否则为未命中。

(3)排序并返回检索结果。令И=И/K，再次计算И/KmodK。如果结果仍为0，则检索计数器count加1；否则搜索结束。在对所有文档执行搜索后，云存储服务器依据count的大小对包含关键词的文档进行排序，并将count和对应文件的下载地址返回给检索用户，以反映不同文件的相关程度。

注意：检索用户并不能获得文档明文，只有数据拥有者将密钥P及秘密数x、g共享给检索用户时，他才能够正确解密并获得原始明文。

3.6 多关键字密文检索方案CRSHE_RMK

(1)检索请求生成。针对安全大素数P和检索关键词Ki(1≤i≤t)，计算检索用户计算关键词密文乘积K=Π(Kigx+RP+RPQ)modQ=Π(Kigx+RP)modQ，然后将K作为搜索请求上传至云存储服务器。

(2)密文检索过程。云存储服务器从加密文件C中依次读取密文分组ci(1≤i≤r)，计算密文分组累乘积И=Πci，然后计算И/KmodK。若结果为0，则表示多关键字检索命中，检索计数器count置1；否则为未命中，count置0。

(3)返回检索结果。在对所有文件执行搜索后，云存储服务器将count值为1的文件下载地址返回给用户。

4 CRSHE方案理论分析

4.1 正确性分析

定理1在CRSHE机制中，持有密钥P、Q及秘密数x、g的用户可恢复明文M。

证明对任意明文分组mi，由于P>mi，因此对应密文c的解密结果Decrypt(c) =cg-xmodP= (migx+RP+RPQ)g-xmodP=mi。显然，将所有分组mi按顺序拼接起来即可还原成明文M。证毕。

□

定理2CRSHE_Enc为全同态加密方案。

证明给定两个分组mi和mj，其对应的密文分别是：ci=migx+RiP+RiPQ和cj=mjgx+RjP+RjPQ，以下分别证明CRSHE机制支持加法同态及乘法同态。

(1)因Encrypt(mi+mj)=(mi+mj)gx+RP+RPQ，另一方面，Encrypt(mi)+Encrypt(mj)=migx+RiP+RiPQ+mjgx+RjP+RjPQ=(mi+mj)gx+(Ri+Rj)P+(Ri+Rj)PQ，故Decrypt(Encrypt(mi+mj))=(mi+mj)gxg-x=mi+mj=Decrypt(Encrypt(mi)+Encrypt(mj))，因此该方案满足加法同态。

(2)因Encrypt(mi*mj)=mimjgx+RP+RPQ，所以：Decrypt(Encrypt(mi*mj))=mimjgxg-xmodP=mimj；此外，Encrypt(mi)*Encrypt(mj)=(migx+RiP+RiPQ)*(mjgx+RjP+RjPQ)g-x=mimjg2x+ (miRjgx+mjRigx+miRjgxQ+mjRigxQ)P+(RiRj+2RiRjQ+RiRjQ2)P2，则Decrypt(Encrypt(mi) *Encrypt(mj))=mimjg2xg-xmodP。考虑到gx是有限半群〈ZP,*〉的幂等元，则g2xmodP=gxmodP，故Decrypt(Encrypt(mi*mj))=Decrypt(Encrypt(mi) *Encrypt(mj))，因此该方案同样满足乘法同态。

由于减法和除法可以由加法和乘法分别实现，因此该方案为全同态加密方案，证毕。

□

4.2 安全性分析

(1)密文数据安全性。

由于服务器只能从用户得到C和Q，服务方只能获得 (mgx+RP)modQ。一方面，密钥P是对服务器保密的，且通过随机数R施加噪声干扰；另一方面，即使服务器通过多组mgx+RP成功猜测到P，但是由于其不知道具体的g及x，因此依然不能获悉原始数据m。可见CRSHE机制通过双重安全机制有效保护了用户数据隐私。

(2)检索关键词安全性。

用户向服务器提交的检索请求是通过P、g及x的转换之后的密文，在无法获得P和g及x的前提下是无法获得关键词明文M的，保证了用户检索关键词的安全性。同时，服务器在执行检索的过程中只是对密文进行操作，全程无法获悉用户数据和关键词的明文，实现了密文检索的功能。

(3)保密参数安全性。

在生成系统保密参数时，必须考虑密钥P要有足够大的密钥空间，以防止密钥P、g、x被穷举攻破。但是,P越大，带来的运算开销将越大。如何在效率和安全性之间达到较好的平衡是本机制需要重点解决的问题之一。

4.3 效率分析

CRSHE机制的检索效率与关键字长度密切相关。对于固定长度的文件，在对明文M进行分组时，分组长度越大，则划分的分组越少，检索循环次数相应越少；反之，则划分的分组越多，检索时需要的循环次数也越多。同时，在分组时有可能正好将关键字划分到不同的分组中，导致不能正确检索到该关键字，因此检索准确率并非100%，而是随着划分组数的增加而减小。如何设计合理的分组长度也是本方案的难点问题之一。

此外，由于CRSHE机制支持多关键词联合查询，因此较其他方案可显著提高检索效率。

5 方案测试与实验分析

5.1 实验环境构建

为了检验方案的正确性与效率，搭建了一个由1个NameNode和15个DataNode组成的Hadoop云存储实验系统。服务端结点采用IBM X3650M2机架式服务器，具有4 GB DDR3内存和2个146 GB SAS硬盘，Ubuntu 10.0.2系统；客户端采用普通PC机，配备1 GB内存和160 GB硬盘，Windows 7操作系统；所有结点连接在百兆局域网中。通过反复实验对比，确定密钥P和大素数Q的长度为512位,关键字长度和明文分组长度均设为32位。

5.2 检索效率测试

通过建立不同关键词数量的索引，对方案的检索效率进行测试，并与经典线性密文检索方案SSKE(Sequential Searching on Keyword Encrytion)[7]进行比较。以100篇纯中文文本文档为测试样本，每个文档平均为2 MB。在测试过程中将关键词长度确定为2个中文字符，对应为32位的二进制数；数量从1个逐步增加到5个。在每种索引关键词数量下分别进行50次检索测试，取其平均时间为最终结果。

将SSKE方案在Hadoop测试平台上进行了代码实现，使用相同的安全参数。由于该方案不支持多关键词索引，因此需要多次执行单关键词索引，然后累加所需时间。测试结果如表2所示。

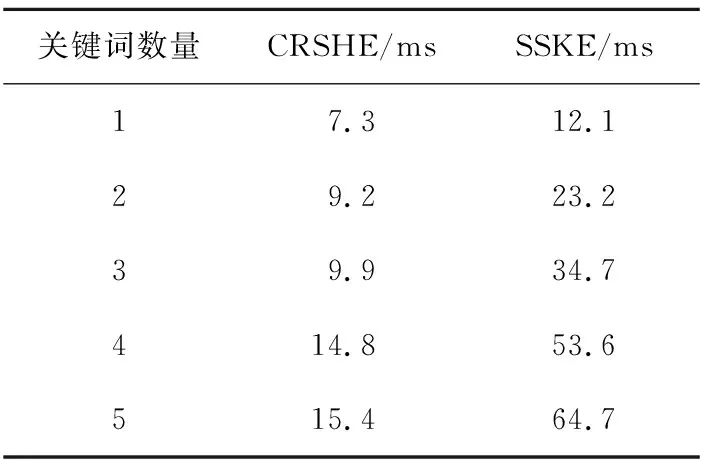
Table 2 Performance comparison between the two retrieval schemes表2 两种不同方案的检索效率对比

可见，两种方案的单关键词检索效率相差不大，CRSHE稍快；但是随着当索引数量增加，CRSHE返回结果所用时间增长较为缓慢，而SSKE方案由于不支持多关键词索引，需要多次执行单关键词索引，故其所需时间大致成线性增长。

5.3 检索准确性测试

如上所述，在密文分组时有可能正好将关键字划分到不同的分组中，导致检索准确率会低于100%。仍以上述100篇文本文档为测试样本，对CRSHE机制的检索准确性进行测试。每个数量随机抽取10种不同的关键字组合，分别进行50次测试并记录平均准确率，测试结果如表3所示。

Table 3 Test result of retrieval accuracy rate表3 CRSHE机制检索准确性测试结果

可见，随着关键词数量增加，CRSHE机制的准确率有一定的下降，但综合检索准确率都在88%以上。

6 结束语

与传统的数据存储方式相比，云存储具有低成本、可扩展、快速伸缩和利用率高等特征，使得云存储得到了越来越多的关注和支持。但是，如果不能妥善解决云存储中的安全问题，特别是基于密文的高效检索问题，将会严重制约云存储应用的可持续发展。本文针对这一紧迫问题，提出一种基于全同态加密的密文检索机制CRSHE，通过两重机制对明文加密，可以在不恢复加密明文信息的情况下实施近似精确的密文检索，并实现了结果的排序。该方案不但保护了使用者的数据安全，同时全同态算法在多关键词检索时能较大地提升检索性能，具有一定的应用前景。