基于VMD-SVD联合降噪和频率切片小波变换的滚动轴承故障特征提取

马增强， 张俊甲， 张 安， 阮婉莹

(石家庄铁道大学 电气与电子工程学院，石家庄 050043)

滚动轴承作为旋转机械中应用最广的关键零部件，其工作状态直接影响机械系统的运行效率及使用寿命,因此，对轴承的故障诊断有重要意义和应用价值。

时频分析方法能提取振动信号时域和频域的局部信息，在滚动轴承故障诊断中有着广泛的应用。典型的时频分布有小波变换、短时Fourier变换、Wigner-Ville分布等[1-2]，但是这些方法都存在着各自的局限性，Yan等[3-4]提出了一种新的时频分析方法——频率切片小波变换(Frequency Sliced Wavelet Transform, FSWT)方法。FSWT通过引入频率切片函数使傅里叶变换具有实现时频分析的功能，能灵活地实现信号的滤波与分割。钟先友等[5]采用形态自相关对信号进行降噪，应用FSWT进行细化分析提取轴承故障特征。段晨东等[6]将FSWT应用到发电机组故障特征提取上，并取得了较好的效果；周福成等[7]将奇异值分解结合FSWT应用到齿轮故障特征提取上，实现了齿轮运行状态的准确判别。研究发现，轴承振动信号中的噪声会降低FSWT的频率分辨率，当信号的信噪比较低时，FSWT不能有效地提取出故障特征，受环境噪声及信号传递路径的影响，滚动轴承故障特征相对于强背景噪声往往表现得非常微弱且通常以调制形式出现难以提取故障特征，因此，对滚动轴承振动信号进行FSWT分析前进行降噪。变分模态分解(Variational Mode Decomposition, VMD)[8]是一种自适应信号分解方法，其实质相当于带通滤波，能有效拾取故障频带，相比于EMD分解，VMD有效克服了EMD所存在的端点效应和模态混叠等现象[9]。

奇异值分解(Singular Value Decomposition,SVD)是一种非线性滤波方法，有着极好的稳定性和不变形[10]。通过构造信号的 Hankel矩阵，并对矩阵进行奇异值分解，选取恰当的奇异值进行信号重构能有效地消除信号中的随机噪声，最大限度地保留有用信息，剔除无用信息，提高信号的信噪比。

本文提出了VMD-SVD联合降噪与FSWT相结合的滚动轴承故障特征提取方法，采用VMD-FSWT对轴承故障信号进行降噪处理，然后对降噪信号进行FSWT和故障特征提取。仿真信号与实测数据分析表明该方法在故障特征提取上有效性和准确性。

1 FSWT基本原理

1.1 FSWT正变换

(1)

令λ=1，尺度因子σ=ω/k，k>0，则

(2)

把k(u-ω)/ω引入频率切片函数(FSF)中，k与ω,u无关，用它来调节变换对时间的灵敏度或对频率的灵敏度，并称之为时频分辨系数。

FSWT常用的FSF为

1.2 FSWT逆变换

FSWT实现了信号的时频分解，其FSWT采用一种简单形式逆变换重构原始信号，它的逆变换为

(3)

(4)

2 VMD-SVD联合降噪方法基本原理

2.1 变分模态分解原理

VMD理论框架是自适应求解约束变分模型最优解，通过不断迭代确定每个IMF的中心频率和带宽，实现信号频域剖分及各个IMFs的有效分离，每个IMF都是一个单分量的调幅-调频uk(t)信号，其表达式为[13]

uk(t)=Ak(t)cos(φk(t))

(5)

VMD的变分问题是寻求K个模态函数uk(t)，k∈{1,2,…,K}，使得所有IMF估计带宽之和最小，约束条件为各模态之和为输入信号f，具体分解步骤如下

(1)通过Hilbert变换计算每个模态函数uk(t)的解析信号，得到其单边频谱

[δ(t)+j/πt]*uk(t)

(6)

(2)对解析信号混合一预估中心频率e-jωkt，将每个模态的频谱调制到相应的基频带

[(δ(t)+j/πt)*uk(t)]e-jωkt

(7)

(3)计算以上解调信号的梯度的平方L2范数，估计出各模态分量的带宽。约束变分模型如下

(8)

(4)引入二次惩罚因子α和Lagrange乘法算子λ(t)，将约束性变分问题变为非约束性变分问题扩展Lagrange表达式如下

L({uk(t)},{ωk},λ(t))=

(9)

利用交替方向乘子算法反复迭代寻求扩展Lagrange表达式的‘鞍点’最小值，最优解为各IMF的{uk}及中心频率{ωk}。

2.2 峭度准则

峭度是描述波形尖峰度的一个无量纲参数，对信号中的冲击特性较敏感。对于一个离散变量x，归一化的4阶中心矩被称为峭度(Kurtosis)，定义为

(10)

式中:E(x-μ)4表示4阶数学期望，μ为均值，σ为标准差。在正常情况下，轴承振动信号的幅值概率密度接近正态分布，峭度值约为3，是平稳或弱平稳过程。但当出现轴承元件点蚀、裂纹等损伤冲击时，信号的幅域参数将发生变化，幅值概率密度函数也将偏离正态分布。所以峭度值越大的IMF中所含的冲击成分与故障信息越丰富，故障特征就易提取[14]。

2.3 奇异值分解

对实际采样信号{xi,i=1,2,…,N},由空间重构理论构造L×K阶的Hankel矩阵

(11)

式中:N为信号长度，K=N-L+1，延时为1，H为轨道矩阵。H的奇异值分解可表示为

H=USVT

(12)

式中:U∈RL×L，V∈RK×K分别为正交矩阵且满足UUT=1,VVT=1；S=diag(σ1,σ2,…,σn),其中σ1,σ2,…,σn为奇异值。

奇异值差分谱描述了奇异值序列变化情况，由于差分序列数值较大，本文选择采用变量Sk表示差分谱[15]

(13)

式中:di=σi-σi+1，t=min(L,K)-1。

奇异值分解后信号的降噪效果与降噪阶次选取有关，若阶次选取过低则信号故障信息可能丢失，阶次过高时，会使得降噪信号仍保留噪声信息，所以选择适当的奇异值有效秩阶次可以起到有效剥离噪声的作用。本文采取文献[16]所提出的一种单边极大值原则，来确定信号的有效秩阶次，从而完成对有用信号的重构和对噪声的消除。

3 基于VMD-SVD联合降噪与FSWT的故障特征提取

工程实际中受环境噪声及信号传递的衰减影响，滚动轴承故障特征相对于强背景噪声往往表现得非常微弱，当信号的信噪比较低时，FSWT不能有效地提取出故障特征，故障信号利用VMD方法处理后，虽然通过峭度准则能筛选包含故障信息最丰富的IMF分量，拾取故障频带，但信号分量中难免存在背景噪声及随机振动干扰，奇异值分解有良好的消噪能力，能最大限度地保留有用信息，剔除无用信息，提高信号的信噪比。因此，提出了基于VMD-SVD联合降噪与FSWT相结合的滚动轴承故障诊断方法。

具体步骤如下：

步骤1 对加速度传感器采集的故障信号进行VMD分解，得到若干IMF；

步骤2 计算各IMF峭度值，根据峭度准则选择峭度值较大的IMF进行信号重构；

步骤3 获取重构信号的Hankel矩阵，进行奇异值分解；

步骤4 根据奇异值的差分谱，选择合适的差分谱峰，由相应的奇异值进行信号重构；

步骤6 针对轴承故障的特点，选零到轴承故障特征频率五倍频作为频率切片区间进行FSWT细化分析，提取故障特征。

4 仿真信号分析

4.1 仿真信号

为验证本文算法的有效性和准确性，使用单位周期脉冲序列，并向其添加强烈白噪声来模拟滚动轴承的单点故障，仿真信号如下

(14)

式中：A=1；衰减系数K为800；u(t)为单位阶跃函数；τi为0.01/fr～0.02/fr之间的随机数；n(t)为白噪声，设定信号的故障特征频率fr=128。

图1(a)中可以看出未加噪声信号是有13个冲击的周期T=7.814×10-3脉冲序列。图1(b)、(c)加入噪声后脉冲信息周期、调制特性完全淹没于噪声中，共振频带基本被噪声信号淹没，无法有效提取故障特征频率。

4.2 仿真信号降噪分析

仿真信号经VMD分解后各IMF中心频率如表1所示，可知当K=5时中心频率相差较大，出现了欠分解现象；当K=7时出现了中心频率相近的模态分量，导致过分解，因此确定模态分量个数K=6，仿真信号的VMD分解结果如图2所示。

从图2可以看出含噪信号经VMD分解后实现了信号频域及各个IMFs的自适应剖分，每个IMF都紧围绕在某一中心频率，各个IMF峭度值如表2所示。IMF2和IMF5峭度值较大，说明包含相对丰富的冲击成分与故障信息。由峭度准则选取该分量合成得到重构信号u(t)。

经VMD分解后重构信号时域及频域波形如图3所示，在时域图中冲击特性谱线更为明显，但脉冲信号周期特性仍受噪声影响较大，频域图中可以较为清晰的看到3 000 Hz及8 000 Hz共振频带，但杂频干扰谱线过多。因此利用奇异值分解对信号u(t)进一步降噪，提高信号信噪比。

表1不同K值各个模态分量的中心频率

Tab.1IMFcenterfrequencycorrespondingtodifferentvaluesofK

模态个数中心频率/Hzu7u6 u5 u4 u3 u2 u1 31 0482 9448 262 41 0492 9685 9277 855 51 0493 0275 8177 93610 502 61 0492 9444 4996 2847 93610 502 76332 9445 0826 9368 44811 05211 480

(a)未加噪信号时域图

(b)含噪信号时域图

(c)加噪信号频域图图1 仿真信号时域及频域图Fig.1 Waveform and spectrum of simulated signals

图2 VMD模态分量波形及频谱Fig.2 Waveform and spectrum of simulated signals

表2 各IMF分量峭度值Tab.2 The kurtosis of each IMF

(a)u(t)时域图

(b)u(t)频谱图

(c)v(t)时域图

(d)v(t)频谱图图3 VMD-SVD联合降噪分析结果Fig.3 The analysis results of VMD-SVD

(a)奇异值分布曲线

(b)奇异值差分谱图4 奇异值及奇异值差分谱图Fig.4 Singular values and difference spectrum

对u(t)的Hankel矩阵进行奇异值分解，奇异值分布曲线及差分谱如图4所示，根据单边极大值原则在图4(b)中自右向左观察在20点处出现第一个最大单边峰值，选择该点为重构信号有效秩阶次对u(t)进行降噪，奇异值降噪后信号v(t)，其时域波形及频谱如图5所示。

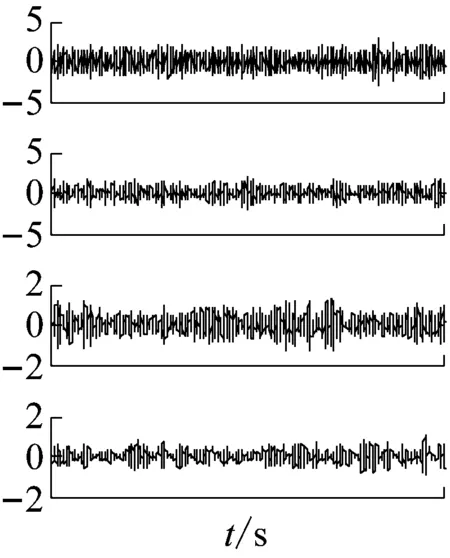
图5 EMD模态分量波形及频谱Fig.5 Waveform and spectrum of simulated signals

对比图3与图1，可以观测到经SVD降噪后时域波形时域信号中调制、周期特性被清楚显示出来，脉冲周期约为7.82×10-3s，频谱图中无关杂频分量被去除，共振频带被最大限度保留。

为对比分析说明VMD-SVD降噪效果，采用EMD-SVD降噪方法对同一信号进行降噪处理。原始信号EMD分解后各模态分量波形及频谱如图5所示，限于篇幅限制只列出了前4个分量波形图，依据峭度准则选取前两个IMF分量重构信号u1(t)，利用奇异值分解对信号u1(t)进行降噪，采用相同方法选取奇异值并对信号进行重构，获取奇异值降噪信号v1(t)如图6所示。

(a)u1(t)时域图

(b)u1(t)频谱图

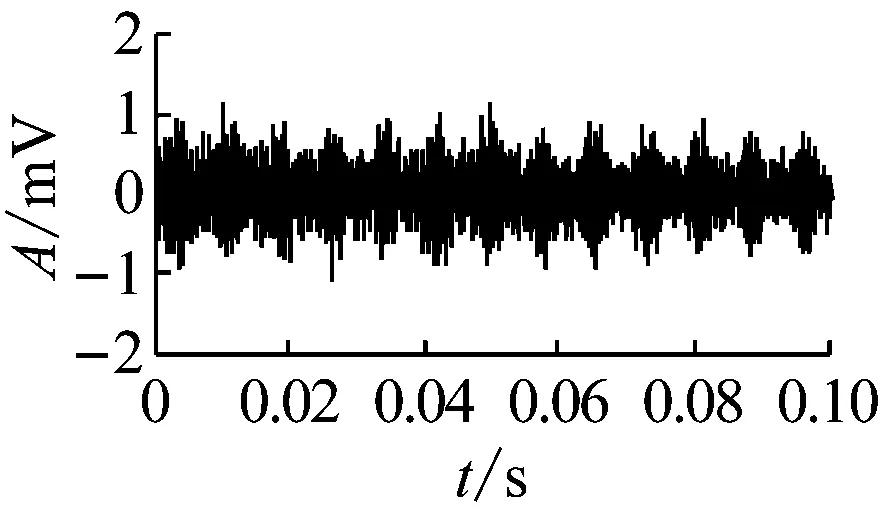
(c)v1(t)时域图

(d)v1(t)频谱图图6 EMD-SVD联合降噪分析结果Fig.6 The analysis results of EMD-ICA

通过图2与图5对比可以看出，EMD分解各模态分量出现了严重的模态混叠，各模态分量的频段分离效果不是很分明，尤其是IMF1，在整个频率范围内几乎都有分量，EMD分解重构信号经SVD降噪后仍在一定程度上受噪声干扰，与图5相比EMD-SVD降噪信号时域图周期性脉冲不太明显，频域图上在4 000 Hz左右有着杂频分量干扰。为了定量地分析两种方法降噪后的去噪效果，选取峭度值(K)、峰值信噪比(PSNR)作为降噪后效果的评价指标，峰值信噪比则反映了信号的去噪能力，峰值信噪比越大则说明去噪效果越好。

4.3 仿真信号FSWT时频分析

表3 降噪结果对比Tab.3 The contrastive results of the two methods

(15)

频率切片区间取[0，600]Hz，图7为降噪信号的FSWT结果。从图7(a)中可以明显看到故障特征频率基频128 Hz及其倍频256 Hz、384 Hz、512 Hz信息，时频分布特征比较清晰，由此可见仿真信号经VMD-SVD联合降噪后能够有效消除噪声干扰，强化了故障冲击特征，能够实现故障特征提取。

为与本文方法进行比较分析，对EMD-SVD降噪信号进行FSWT分析如图7(b)所示。从该图中可以看到故障特征频率基频128 Hz、二倍频256 Hz，高频信息不能很好被提取，时频分布特征不够清晰，由此可见本文方法在降噪与故障特征提取上效果更好。

(a)VMD-SVD降噪信号FSWT时频图

5 实测信号分析

5.1 实验装置与数据采集

通过图8所示QPZZ-Ⅱ旋转机械故障试验台采集滚动轴承故障数据，用内圈点蚀故障号对本文所提方法进行验证，将CA-YD-188型传感器利用磁座安装在支座上，信号的采样频率为25.6 kHz，轴承转速为317 r/min，转频为5.28 Hz理论内圈故障特征频率为37.8 Hz。

滚动轴承发生内圈故障时，内圈转动所引起的冲击振动呈现出周期性的变化，这种周期性变换使得振动信号产生以转速为调制频率的调频调幅现象，高频振动序列为其高频载波。内圈故障信号的时域和频域波形如图9所示，从图中可以看出时域波形有冲击但并不突出，频谱图谱线成分丰富不能确定故障特征频率及故障类型。

轴承型号 中径D/mm滚子直径d/mm接触角α/(°)滚子个数z转速r/minN205E38.57.5012317

5.2 实测故障数据分析

滚动轴承早期故障特征通常比较微弱，由于背景噪声及传递路径衰减因素的干扰，会对特征信息的提取带来严重阻碍。故障信号经VMD分解后选取峭度值最大的模态分量实质相当于对故障信号做带通滤波处理，拾取了故障特征相对丰富的频带，而早期故障特征信息的微弱特征并未改变，因此需对重构信号进一步奇异值降噪以最大限度保留有用信息，剔除无关分量干扰从而提高故障信号信噪比。

图9 内圈故障信号波形及其频谱

Fig.9 Inner ring fault signal waveform and its spectrum

采用表2方法对故障信号进行VMD分解，根据峭度准则选取峭度值最大的前两个IMF进行合成如图10(a)、(d)，拾取了高频共振频带，说明在10 kHz频带故障信息最为丰富，VMD分解能够克服模态混叠，实现各IMFs频率的有效分离。

利用奇异谱分解对VMD分解后合成信号进行降噪分析，重构信号Hankel矩阵奇异值分解后奇异值分布如图10(b)、(e)所示，通过计算奇异值差分谱依据文献方法选取前72个奇异值对信号进行重构，重构信号波形如图10(c)、(f)所示。

(a)IMF合成信号波形

(b)奇异值分布曲线

(c)VMD-SVD降噪信号波形

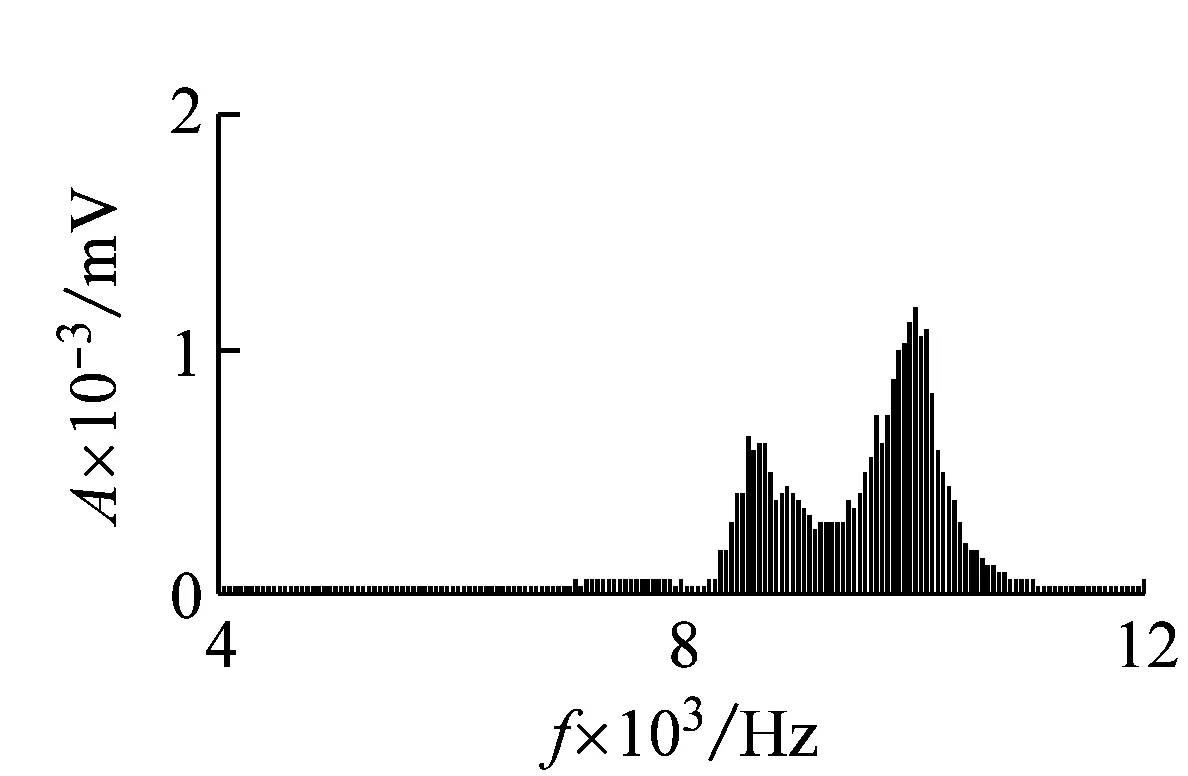
(d)IMF合成信号频谱

(e)奇异值差分谱

(f)VMD-SVD降噪信号频谱图10 内圈故障信号降噪结果Fig.10 Inner ring fault signal waveform and its spectrum

根据文献[15]所提出的单边极大值原则确定信号的有效秩阶次为72，对比图10(c)、(f)与(a)、(d)可以看出VMD-SVD降噪信号时域冲击特征更为明显，频域故障谱带更为精确，说明降噪信号有效保留了原始故障信号的故障信息，去除了噪声及杂频干扰为下一步FSWT故障信息提取创造了有利条件。

轴承内圈故障信号经VMD-SVD降噪后，按式(15)选择FSWT参数，频率切片区间取[0，200]Hz，图10为降噪信号的FSWT结果。作为对比采用FSWT对EMD-SVD降噪信号进行分析，从图11(a)、(c)的时频图中可以发现明显的38 Hz故障区域，对应轴承内圈故障特征频率，同时存在76 Hz、114 Hz、152 Hz等频率成分，这正好对应故障频率的二倍频、三倍频、四倍频；在基频带左右存在32.8 Hz、43.2 Hz边频带，这与内圈故障特征频率被转频所调制的特性相符，进一步验证了故障位置为轴承内圈。

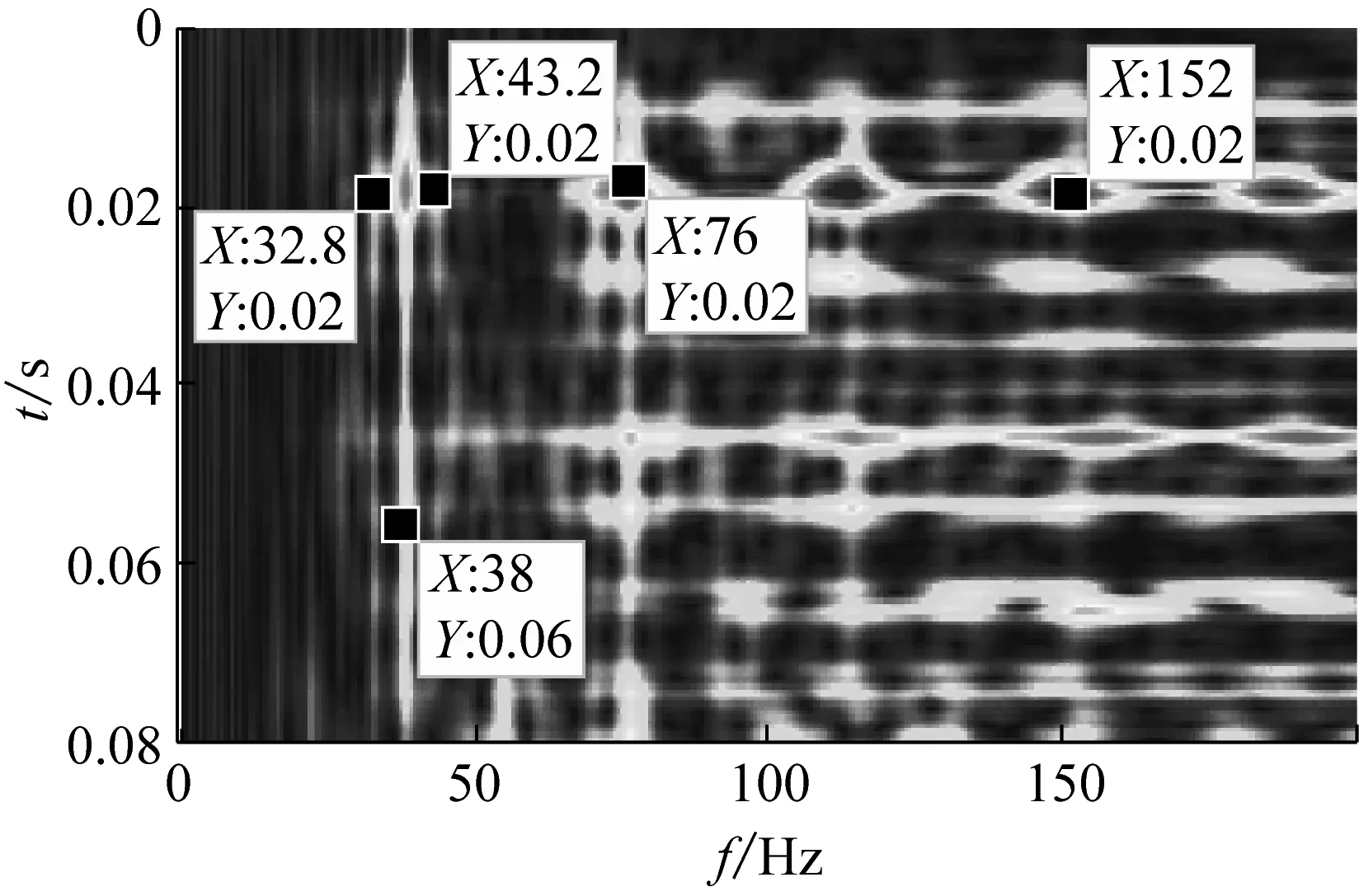
(a)VMD-SVD时频图

(b)EMD-SVD时频图

(c)VMD-SVD时频幅值图

(d)EMD-SVD时频幅值图图11 轴承内圈故障信号的FSWT结果Fig.11 FSWT results bearing inner ring fault signal

对比图11(a)、(c)与(b)、(d)可知，由于EMD分解各IMF分量间的模态混叠等，不同分量间频带不能实现较好分离，在FSWT时频图中虽能提取故障特征频率及部分倍频但效果并不清晰，杂频谱线及噪声干扰过多，突出了本文方法的优越性。

6 结 论

针对频率切片小波变换在强背景噪声中提取故障特征不足的问题，提出了基于VMD-SVD联合降噪和频率切片小波变换的滚动轴承故障特征提取方法，变分模态分解是一种新的信号自适应方法，其克服了EMD方法中的模态混叠等问题，能有效拾取故障频带，经SVD降噪后能保留有用信息，消除背景噪声干扰。主要结论如下:

(1)将VMD-SVD联合降噪与FSWT相结合，能准确的从故障信号中提取故障特征频率，仿真信号与实测数据分析验证了该方法有效性。

(2)故障信号进行VMD分解后可有效选择故障频带，经SVD降噪后能最大限度保留有用信息，去除背景噪声干扰，降噪效果优于EMD-SVD联合降噪分析。

(3)时频分析方法结果表明，相比于EMD-SVD降噪方法，本文时频分布特征更加清晰，在滚动轴承故障特征提取上效果更加准确，具有明显优势。

VMD在故障信号分解及故障频带选取效果有赖于惩罚因子α和模态分量K的事先给定，本文下一步的研究工作是对VMD参数的优化及自适应选取。