基于支持向量机与粒子滤波的刀具磨损状态识别

程 灿， 李建勇,2， 徐文胜， 聂 蒙,2

(1. 北京交通大学 机械与电子控制工程学院，北京 100044； 2. 载运工具先进制造与测控技术教育部重点实验室，北京 100044)

刀具在加工工件的过程中，自身不断磨损，其磨损状态对加工工件的质量、加工过程的效率和成本有显著的影响。工业生产统计表明，刀具失效是造成机床故障的重要原因[1-2]，Kurada等认为由刀具失效引起的数控机床的停机时间约占其总停机时间的20%。加工过程的中断，可能造成工件报废，甚至整个生产系统的瘫痪，影响生产效率。工业生产之外，在一些特殊的场合，刀具磨损状态的监测尤为重要，例如：叶轮是叶轮机械中的核心部件，需要在高温高压的工作环境下承受较大的工作载荷[3]，其加工质量要求较高，而铣刀的磨损状态影响叶轮的加工质量，因此需要对加工过程中铣刀的磨损状态进行监测；利用砂轮或者砂带进行钢轨打磨时，如果磨具失效，钢轨加工质量不符合验收标准，则需要更换钢轨，耗费大量人力物力，成本高昂，同时可能会影响铁路运输的正常运行，造成严重后果。总之，刀具磨损状态的实时监测是保证工件加工质量、提高良品率，增强加工系统的可靠性，提升生产效率的关键技术之一。

刀具磨损状态监测方法主要分为两种：直接监测方法和间接监测方法。刀具磨损状态识别是指利用间接监测方法时，将传感器信号输入数学模型，得到刀具磨损状态的过程。目前，刀具磨损状态识别的方法主要有人工神经网络(Artificial Neural Network，ANN)、模糊逻辑(Fuzzy Logic，FL)、隐马尔科夫(Hidden Markov Model，HMM)、支持向量机(Support Vector Machine，SVM)等。机械加工过程中，刀具与工件在接触区域的相互作用复杂，一方面切屑形成过程中，工件材料弹性变形及塑性变形形成对刀具的抗力；另一方面切屑及工件表面与刀具之间存在摩擦阻力，其中切屑与刀具的摩擦阻力既有在黏结区发生的内摩擦又有在滑移区发生的滑动摩擦，同时在切削过程中会产生积屑瘤，改变刀具与工件的接触状态[4]。因此，加工过程中，刀具的磨损与切削力、振动等信号间呈现显著的非线性关系。在实际加工过程中，传感器信号不仅受刀具磨损程度的影响，同时受加工参数、加工设备机械结构、工件材料、刀具材料及尺寸等各种因素影响，因此在各种特定条件下获取的样本数一般较少，受限于实验成本，实验研究中样本稀少的问题更为突出。综上所述，刀具磨损与监测信号间的非线性以及模型训练样本有限是刀具磨损状态识别的两个突出问题。

支持向量机分为支持向量分类机(Support Vector Classification，SVC)与支持向量回归机(Support Vector Regression，SVR),是在20世纪90年代由Vapnik等[5-6]提出的一种基于统计学习理论的机器学习算法。SVM作为统计学习中一种用来解决有限样本的学习算法，在解决非线性、小样本、多维数问题时表现出了很多优良的特性，因此一些学者将SVM应用到了刀具磨损状态识别中。

Salgado等[7]通过监测声信号，利用SVM方法回归得到了切削力和刀具磨损量，并且发现ANN和SVM在大量训练集上的正确率相近，当训练集减少时SVM拥有较高的正确率和较强的泛化能力。Benkedjouh等[8]利用小波包分解技术提取监测信号特征，并利用主成分分析(PCA)与等距映射算法(ISOMAP)进行特征削减，之后利用SVM进行磨损量的回归。张栋梁等[9]在利用混沌时序分析技术提取与磨损相关特征的基础上，利用SVM分类技术识别刀具的不同磨损状态。

为了提高SVM的学习能力，在进行SVM模型训练时，需要选择合适的输入特征和模型训练参数，一些学者分别在特征选择和SVM参数选择方面做了很多工作。袁敏利用果蝇优化算法进行铣削力特征选择[10]。于明等[11]、刘路等[12]分别在各自的论文中将人工蜂群算法用于优化SVM的惩罚因子C、径向基核函数参数γ，取得了较好的效果。上述研究中，特征选择和训练参数选择被分开进行，实际上SVM的输入特征和训练参数之间是紧密联系、相互关联的，因此本文建立了一种双层规划模型，并组合遗传算法和人工蜂群算法进行求解，使输入特征和模型参数能够协同优化，同时达到最优，从而获得学习能力更强的SVM模型。

为了提高SVM、神经网络等机器学习方法的识别精度，一些学者利用滤波的方法对回归得到的结果进行修正。Peel[13]首先利用三种不同类型的神经网络预测涡轮发动机的剩余寿命，然后利用卡尔曼滤波进行三种神经网络预测结果的融合，并且在模型中利用预测点之前的估计值进行当前预测值的修正，由于当前时刻的剩余寿命与前一时刻的剩余寿命之间有非常明确的递减关系，因此系统的状态转移模型符合卡尔曼滤波的线性假设，滤波取得了较好的效果，集成了卡尔曼滤波的神经网络方法比单一的神经网络方法在准确度方面的性能提升了8.5%。李威霖等[14]将卡尔曼滤波应用到了刀具磨损状态识别中，为了建立系统的状态转移模型，作者假设刀具的磨损量随时间均匀变化，经过滤波之后，两个样本的误差分别从0.656 4 mm降到0.345 8 mm、从0.642 5 mm降到0.385 5 mm，取得了显著的效果。

众多学者的实验结果表明刀具的磨损并不是均匀的，而是呈现较强的非线性[15]，因此本文采用非线性的粒子滤波(Particle Filter，PF)技术对刀具磨损量识别值进行修正。本文在上述研究的基础上，针对刀具磨损状态识别中的非线性与样本有限的问题，提出利用粒子滤波与支持向量机集成的方法进行刀具磨损状态的识别。实例验证结果表明，在小样本情况下，该方法具备良好的学习能力，能够精确地识别刀具的磨损量。

1 刀具磨损监测实验及特征提取

1.1 刀具磨损监测实验

在评定刀具材料的切削性能和试验研究时，一般以刀具表面的磨损量作为衡量刀具的磨钝标准。ISO标准统一规定以1/2背吃刀量处的后刀面上测定的磨损带宽度VB作为刀具的磨钝标准。因此，本文采用刀具后刀面磨损量(VB)表征刀具的磨损状态，通过监测切削力信号、振动信号、声发射信号，识别刀具的后刀面磨损量。

为了验证本文方法的有效性，铣削实验数据采用美国纽约预测与健康管理学会(Prognostics and Health Management Society, PHM)2010年高速数控机床刀具健康预测竞赛的开放数据，竞赛数据对所有研究者公开[16]。实验中采用的加工参数及信号采集参数如表1所示，实验平台如图1所示，在高速数控机床的进给方向(X)、主轴径向(Y)、主轴轴向(Z)安装了加速度传感器，在夹具及工件上安装了测力仪及声发射传感器。实验设备型号如下

机床：高速数控机床Röders Tech RFM760；

测力仪：Kistler 9265B三向测力仪；

振动传感器：Kistler 8636C振动传感器；

声发射传感器：Kistler 8152声发射传感器；

电荷放大器：Kistler 5019A多通道电荷放大器；

铣削材料：不锈钢HRC52；

刀具：球头硬质合金铣刀；

采集器：NI DAQ PCI 1200采集卡；

磨损测量器：LEICA MZ12显微镜

表1 实验参数Tab.1 Parameters of experiment

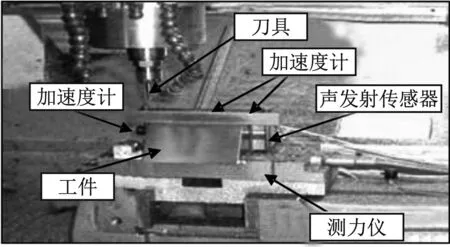
图1 刀具磨损监测实验装置Fig.1 Experiment device of tool wear monitoring

采用六把铣刀(C1,C2,C3,C4,C5,C6)进行全寿命磨损实验，每把铣刀在表1所示的加工参数下对相同的工件进行315次端面铣，每一次端面铣的长度为108 mm，一次端面铣记为一次走刀。记录每次走刀过程中的传感器信号，并且每次走刀之后采用LEICA MZ12显微镜测量三个切削刃的后刀面磨损量作为刀具磨损结果。由于加工工件为方形，所以每次走刀的时间相等，因此直接采用走刀数代替切削时间。刀具C4三个切削刃在315次走刀过程中的后刀面磨损量变化曲线如图2所示。本文的任务是通过下文所建立的模型通过当前走刀的监测信号识别出当前走刀的三个切削刃磨损量中的最大值。

图2 C4切削刃后刀面磨损量变化曲线Fig.2 Correlation between VB and tool degration

1.2 实验信号特征提取分析

信号特征包括信号的时域特征、频域特征、时频域特征。其中时域特征包括均值、方差(标准差)、均方根值、功率、峰值、峰谷值、峰态系数(Kurtossis系数)、偏态系数(Skewnessis系数)、自相关系数等特征，频域特征包括主频幅值、频段能量、功率谱的统计特征等，时频域特征包括小波系数，小波包能量等。本文的重点在于采用双层规划框架的支持向量机回归以及磨损量回归结果修正两个方面，在特征提取方面未做深入的研究，只是提取常用的一些时域和频域特征。

经过对多种时域信号特征的可视化分析之后，提取信号的六种时域特征：均值、均方根值、标准差、峰值、峰谷值、峰态系数(Kurtossis系数)。

经过频谱分析之后，发现在173 Hz、521 Hz、1 042 Hz出现峰值。其中：173 Hz为刀具转频，521 Hz为刀具齿频，在磨损后期每一个切削刃进行切削时信号中会产生两个波峰，频率为1 042 Hz，由于频率521 Hz的切削刃波形的周期性逐渐淹没了频率为173 Hz的刀具旋转的周期性，因此只提取521 Hz和1 042 Hz两个频率能量值。由于存在加工测量时系统噪声以及傅里叶变换时的能量泄露，实际提取的是520～522 Hz，1 041～1 043 Hz两个频带的能量。

实验监测了三个方向的切削力信号、振动信号以及声发射信号七个信号，分别提取每个信号的上述时域和频域八个特征，总共提取出56个备选特征。

2 刀具磨损状态识别建模

2.1 基于双层规划的SVM建模

PHM Society(2010)公布了C1、C4和C6的后刀面磨损量，为了检验本文提出方法的有效性，使用交叉验证的方式检验，即做三组实验验证算法：第一组利用C1和C4作为训练样本，识别C6的磨损量；第二组利用C1和C6作为训练样本，识别C4的磨损量；第三组利用C4和C6作为训练样本，识别C1的磨损量。因此，实际的训练样本只有两个，但是刀具监测信号特征与磨损量之间的映射关系又非常复杂，所以本文采用在解决非线性、小样本、多维数问题时表现出很多优良特性的支持向量机算法进行磨损量的回归。

在训练支持向量机模型时需要解决两个关键问题：一是支持向量机模型的回归精度受其算法参数(惩罚因子C，相对敏感度ν，高斯核函数参数γ)影响较大，为了获得泛化能力强的模型需要选取合适的参数；二是通过上一部分的时域和频域分析，提取出多维的信号特征，这些特征中不仅包含了有用特征，而且包含了冗余特征，冗余特征不仅降低了模型的识别精度而且增加了计算的复杂度，因此模型训练之前需要进行特征选择。以上两个问题实际上是两个优化问题：模型参数的优化和输入特征的优化，为了使输入特征和模型参数能够协同优化，同时达到最优，从而获得识别精度更高的SVM模型，本文利用双层规划理论建模，实现SVM输入特征选择和SVM模型训练参数的协同优化。

本文建立的支持向量机输入特征与参数优化双层规划模型如下

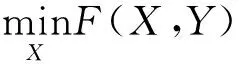
(1)

s. t.xi∈(0，1)，i=1,2,…,N

(2)

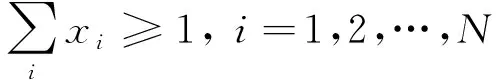
(3)

其中Y是下面问题的解

(4)

s. t.y1≥0

(5)

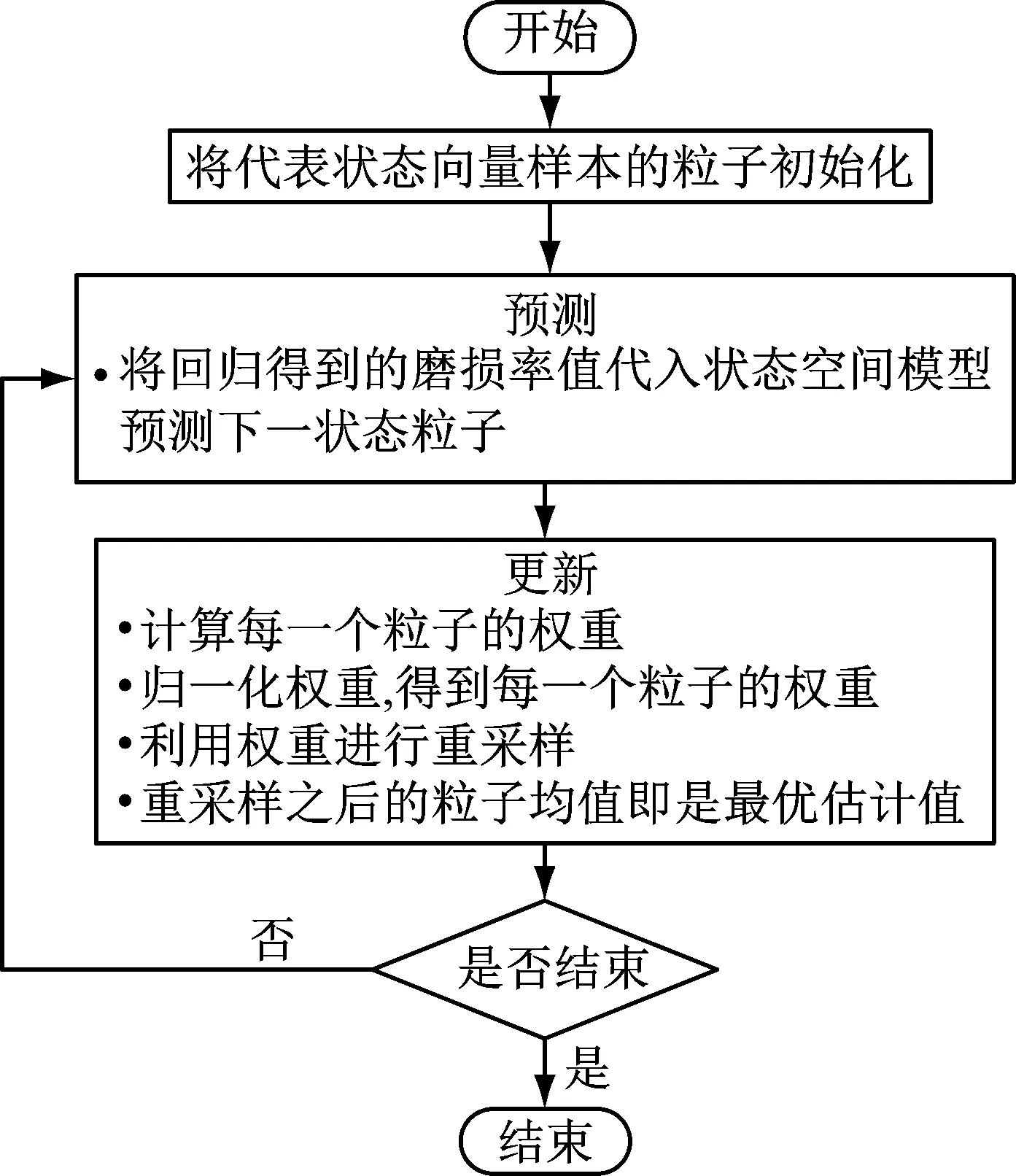
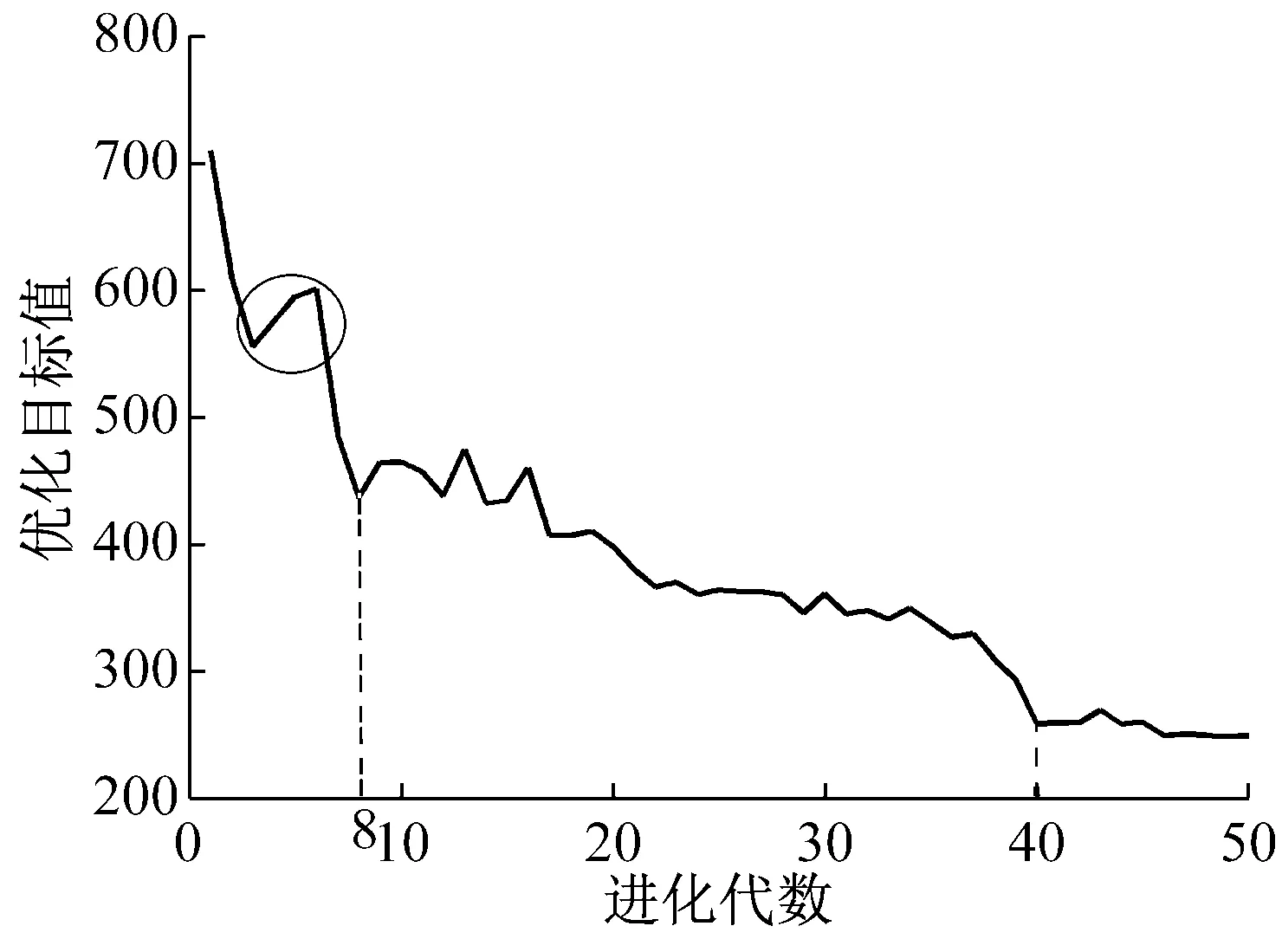
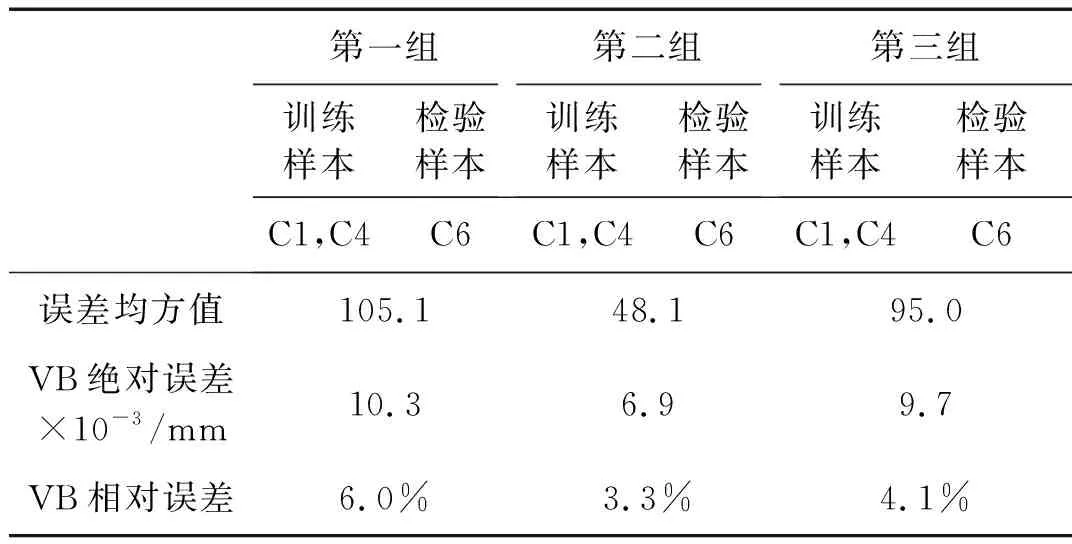
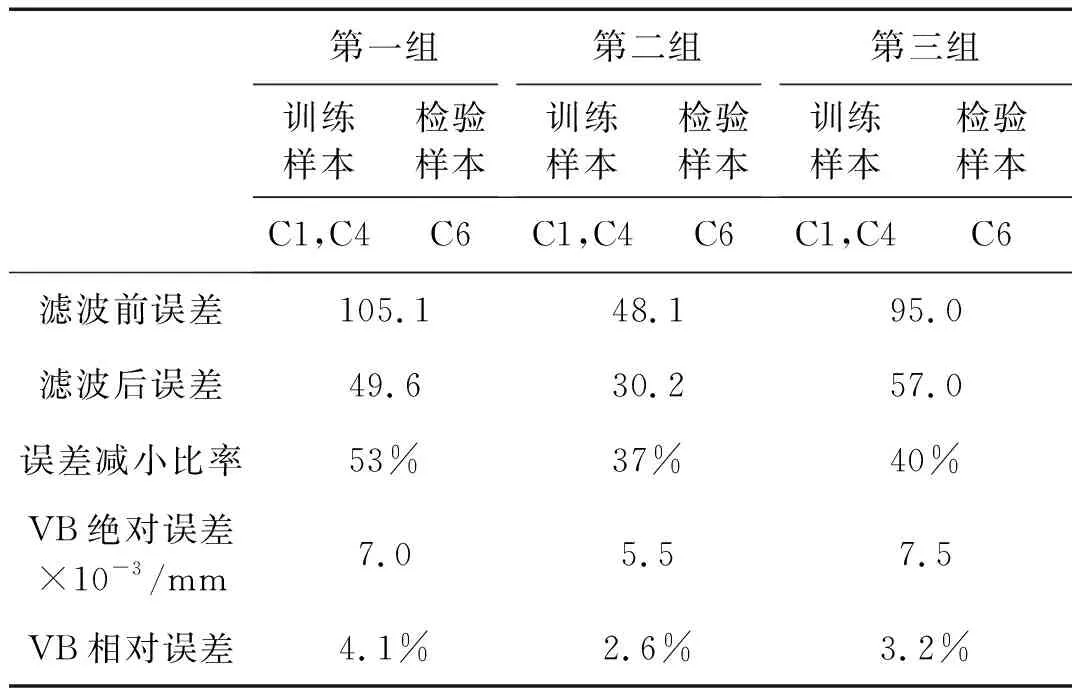
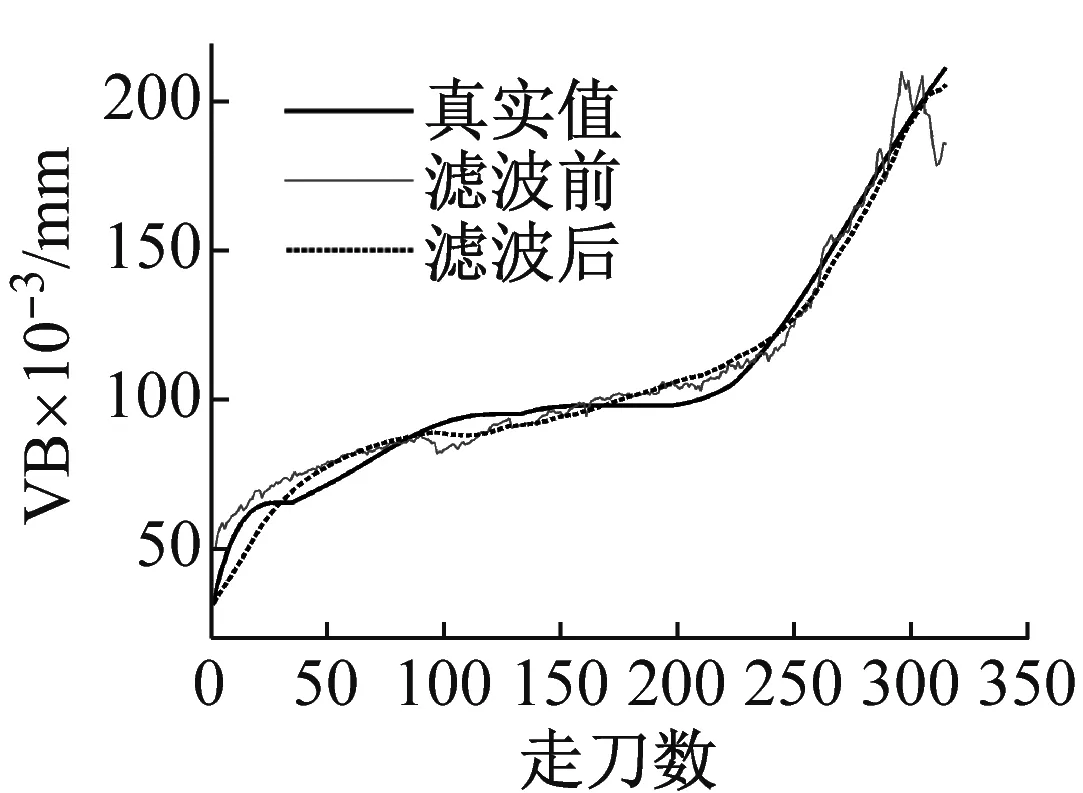
0

(6)

(7)

其中：上层变量X=(x1,x2,…,xN)，N=56，xi=1代表第i个特征被选中作为SVM训练模型的输入。下层变量Y=(y1,y2,y3)表示SVM模型参数集，y1表示惩罚因子C，y2表示相对敏感度ν，y3表示核参数γ。上层的目标函数F和下层的目标函数f的值均为SVM磨损量识别误差的均方值。上层约束中，式(2)约束表示代表每个特征的变量是一个二值变量，式(3)约束表示至少有一个特征作为SVM模型的输入。下层约束分别表示每个参数的上下限。

本文模型的变量是混合型变量，既有上层规划的离散二值型变量X，又有下层规划的连续实数型变量Y，对于上层规划来说，是一个组合优化问题，遗传算法非常适合解决组合优化问题；对于下层规划来说，是一个实数域上的优化问题，因此采用鲁棒性强，全局收敛优势明显的人工蜂群算法进行求解。因此本文通过组合遗传算法和人工蜂群算法，求解所建立的双层规划模型。

2.1.1 基于遗传算法的特征选择

遗传算法主要包括种群初始化、种群适应度计算、种群进化这三个过程。

种群初始化主要是对种群中的个体进行染色体编码，本文染色体采用二进制编码，长度为56，具体结构如图3所示。其中1～7编码位对应七种信号的均值，8～14编码位对应七种信号的均方根值，15～21编码位对应七种信号的标准差，22～28编码位对应七种信号的峰值，29～35编码位对应七种信号的峰谷值，36～42编码位对应七种信号的Kurtossis系数，43～49编码位对应七种信号的521 Hz频率的能量，50～56编码位对应七种信号的1 042 Hz频率的能量。

图3 染色体编码示意图Fig.3 Schematic diagram of chromosome code

种群适应度计算指的是计算种群中所有个体的适应度，在计算个体适应度之前，需要对个体的染色体进行解码，本文中的解码操作指的是提取出个体染色体中编码值为1的码位所对应的特征，作为下层SVM的输入。下层规划得到的模型的识别误差均方值作为个体的适应度。

种群进化包括交叉、精英保留、变异以及为了防止算法局部收敛而进行的引入新个体的操作。其中，交叉操作采用单点交叉的方式进行。染色体交叉率指的是交叉点前的基因位数与染色体总长度的比率。染色体变异率指的是个体染色体中变异的位数的比率。各部分的组成比例见表2。

当种群的进化代数达到最大进化代数时，算法结束。算法的参数如表2所示。

2.1.2 基于人工蜂群算法的SVM参数优化模仿自然界中蜂群采蜜过程中的分工协作机制而设计出的一种优化算法。由于其控制参数少、易于实现、全局搜索能力强、鲁棒性强等特点，已成为群体智能领域的研究热点之一。本文将ABC算法作为下层规划的求解算法，用于优化SVR的参数：惩罚因子、相对敏感度、径向基核函数参数。

人工蜂群算法由Karaboga等[17-18]于2005年提出，蜜蜂是一种社会性群居动物，个体间分工明确，虽然单个个体的行为简单，但是个体间通过信息交流，相互协作，使得整个群体表现出复杂的智慧行为。蜜蜂以跳舞的方式交流蜜源信息，个体在获取其它个体信息的基础上，按照自身的角色分工，做出自身的行为决策。整个搜索模型有两个基本要素：蜜源和蜜蜂。蜜蜂按照角色分工可以分为引领蜂、跟随蜂和侦查蜂，每种蜜蜂都有自己的行为方式。

表2 遗传算法参数表Tab.2 Parameters of GA

在整个寻优过程中，引领蜂用于维持优良解；跟随蜂用于加速解的收敛；侦查蜂用于增强蜂群摆脱局部最优，全局搜索的能力。算法中的参数取值如表3所示。具体编码实现时，首先利用统一建模语言(Unified Modeling Language，UML)对引领蜂、跟随蜂、侦查蜂进行建模，之后在MATLAB中利用面向对象编程技术(Object Oriented Programming，OOP)实现。

双层规划的整体求解流程如图4所示。由图4可以看出，上层遗传算法中种群的每一个个体进行适应度计算时均需要利用下层的人工蜂群算法进行一次SVM的参数优化，优化完成后将最优的SVM模型的误差均方值返回上层，作为上层种群个体的适应度。由于采用了两层的优化算法，算法计算时间较长，为了减少计算时间，使用MATLAB的并行计算工具箱，并行计算种群的个体适应度。并行计算时，设置30个并行计算单元(worker)，计算时间由84小时左右，缩短为16小时左右。时间的缩短与并行计算单元的增加并不是线性关系，主要是因为每个个体的适应度计算时间不同，由此造成的计算单元负载不均。

表3 人工蜂群参数取值表Tab.3 Parameters of ABC

图4 双层规划求解算法整体流程图Fig.4 The whole flow diagram of solving algorithm of bilevel programming model

2.2 基于粒子滤波修正的SVM建模

在实际加工过程中，刀具磨损程度不断加深，刀具的磨损量是单调递增的，但是经过SVR回归得到的磨损量是波动的，这与真实加工过程中刀具磨损量的变化是不相符的。造成这种矛盾的原因一方面是利用SVR模型近似刀具磨损过程时无法避免地产生误差，另一方面就是在进行磨损量的回归时只利用了当前走刀监测数据中提取出的特征信息，而没有利用上一时刻的刀具磨损信息。因此本文利用粒子滤波算法，融合从开始到当前时刻所有的监测数据信息，并且充分利用刀具的监测信号，提取出与后刀面磨损速率相关的信息，从而得到精度更高的磨损量识别值。

本文的状态空间模型如下。

首先，将SVR的回归值作为真实磨损量的一个量测值，建立系统的量测模型。

yk=xk+vk

(8)

式中：xk是k时刻刀具的真实后刀面磨损量；yk是利用支持向量机回归得到的k时刻刀具的后刀面磨损量识别值；vk是磨损量回归模型的误差，假设其服从正态分布。

然后，利用k时刻与k+1时刻磨损量的关系建立系统的状态转移模型

xk+1=xk+rk+wk

(9)

式中：rk是k时刻至k+1时刻的平均后刀面磨损率，其得到的方法与刀具的磨损量回归类似，也是由k时刻至k+1时刻的监测数据的特征输入SVR模型得到，这种建模方式充分挖掘出了k时刻至k+1时刻的监测数据中与磨损率相关的信息；wk是磨损率回归模型的误差，假设其服从正态分布。

从上述模型可以看出，粒子滤波不仅融合了从开始到当前时刻所有的监测数据信息，而且同时从k时刻至k+1时刻的监测数据中提取出了磨损量和磨损率的信息，最大限度地挖掘了监测数据中的信息。图5是本文实现粒子滤波算法的流程图。

图5 粒子滤波流程图[19]Fig.5 The flow diagram of PF

3 实验结果与分析

本文采用上述交叉验证的方式验证算法的有效性，优化算法中的优化目标是三组实验的磨损量识别误差均方值的总和。

3.1 基于双层规划的SVM结果与分析

上层遗传算法优化目标的变化曲线如图6所示。

图6 遗传算法优化目标的变化曲线Fig.6 Correlation between optimal object and evolution generation of GA

由图6可知，1～8代目标值减小迅速，优化效果明显；8～40代目标值逐渐减小；40代之后，算法已经收敛，优化目标值达到最优。当遗传算法采用精英保留策略时，优化目标值不会变差，但是由图6可以看出在优化过程中，目标值会局部变大，如图中圆圈标示出的3～6代的种群最优目标值，其原因就是算法中上层个体的适应度值是下层人工蜂群算法的优化目标值，下层人工蜂群算法并不能保证每次找到的最优解都完全相等。为了使上层个体适应度值计算更加准确，就需要使下层的人工蜂群算法每次收敛的值尽可能相等，即下层算法的鲁棒性更强，这就要求下层算法的进化代数尽可能大，但是下层进化代数过大时，会导致运算时间过长。本文在综合考虑下层算法的鲁棒性和运算时间的要求后，将下层的进化代数确定为30，由图可以看出，虽然优化曲线会有局部的上升，但是整体逐渐下降，下层算法的鲁棒性已经满足了上层算法对个体适应度的计算要求。

表4展示了在每一代种群最优秀的五个个体，共250个个体中，出现次数最多的十个特征，这些特征在寻优过程中出现的次数较多，说明其对后刀面磨损量的变化较为敏感。比如：编码位为5的特征，即Y方向振动均值，在250个个体中出现了239次。

表4 较敏感特征的选中次数Tab.4 Chosen time of sensitive features

经过优化，得到的最优个体所代表的SVM输入特征组合是{1,5,17,19,21,24,25,29,47,56}，可以看出这个最优输入特征包含了表中的九个特征，并不完全是表中十个特征的简单组合，这也说明了特征间的组合优化效应的存在。

下层规划求解算法，即人工蜂群算法的优化目标变化曲线如图7所示。由图中可以看出在15～23次寻优中出现了一次持续时间较长的局部收敛，28次寻优之后逐渐稳定，但是收敛的时间并不是很长，因此并不能保证全局收敛，得到全局最优解。

人工蜂群算法在第1,10,20,30次寻优时蜜源的空间分布如图8所示。第1次寻优时，蜂群在空间中随机分布；第10次寻优时，蜂群已经有了聚集的趋势；第20和30次寻优时，聚集的趋势已经比较明显，说明算法已经收敛。算法在第20次局部收敛之后能够继续优化，也说明了其具有摆脱局部收敛的能力。

图7 人工蜂群算法优化目标变化曲线Fig.7 Correlation between optimal object and evolution generation of ABC

(a) 第1次寻优解的空间分布

(b) 第10次寻优蜜源空间分布

(c) 第20次寻优蜜源空间分布

(d) 第30次寻优蜜源空间分布图8 解的空间分布Fig.8 The space distribution of solutions

三把刀具识别误差均方值的和的最终优化结果为248，具体的识别误差如表5所示。其中，VB绝对误差是误差均方值的平方根，代表每次走刀VB识别值与真实测量值的误差，相对误差指的是绝对误差相对于VB最大真实测量值的大小。

表5 SVM识别结果Tab.5 The recognition result of SVM

3.2 基于粒子滤波修正的SVM结果与分析

粒子滤波的结果如表6所示，三把刀具识别误差均方值分别减小了53%，37%，40%。最终的识别结果如图9所示，黑色实线表示通过显微镜测量的VB真实值，蓝色实线表示在使用粒子滤波之前，由支持向量机回归得到的VB值，虚线表示由粒子滤波方法修正支持向量机回归结果后得到的VB最终识别值。

表6 滤波前后识别结果对比Tab.6 The recognition result before and after filtering

由图9中的结果可以看出：滤波之后的磨损量识别值的波动比滤波之前明显减小，并且单调性较明显，更加符合磨损值真实的变化规律。为了探究本文提出方法在使用单一信号时的识别效果，进行了只使用三向切削力信号进行刀具后刀面磨损量的识别实验，将三向切削力特征作为特征选择的特征集合。通过分析结果发现：本文提出的方法只利用切削力信号仍然可以识别出刀具磨损状态，只是相比于使用三种信号的识别结果，当只使用三向切削力时，识别精度会有所下降。

(a) C1滤波前后磨损量识别结果对比

(b) C4滤波前后磨损量识别结果对比

(c) C6滤波前后磨损量识别结果对比图9 滤波前后磨损量识别结果对比Fig.9 The recognition result before and after filtering

4 结 论

本文提出了一种基于支持向量机和粒子滤波的刀具磨损量识别方法，在提高小样本情况下刀具磨损量识别精度方面取得了令人满意的结果。结果表明：遗传算法能够针对SVM的回归特性，选取适合SVM输入的特征组合；人工蜂群算法兼顾了全局搜索和精确寻优，在SVM参数选取方面表现出优良的性能；双层规划模型，使得输入特征和SVM参数能够协同优化；粒子滤波是磨损量识别关键的一步，在充分利用当前走刀的监测数据的同时，融合之前走刀的监测数据信息，并且在模型中体现了磨损量的单调变化这一规律，使得模型的识别精度显著提高。