基于小波变换模改进Perona-Malik模型的强噪声信号滤波算法

毋文峰， 陈小虎

(1.中国人民武装警察部队警官学院 管理科学与工程系,成都 610213；2.中国人民解放军火箭军工程大学 装备管理工程系,西安 710025)

机械振动信号在产生、传输和记录过程中，由于生成系统和介质的原因，经常会不可避免地受到各种噪声的干扰，使信号的分辨率下降，重要的细节特征受到影响，甚至信号失真，因此，在进一步的奇异性检测、特征提取前，有必要采取适当的方法来降低或去除信号噪声。去噪是机械振动信号处理中一个非常重要的预处理过程，已有国内外诸多专家学者在深入研究这一问题。

目前，小波变换是最为重要的机械振动信号去噪方法之一[1]，已得到了广泛深入的研究和应用。包广清等[2]针对随机噪声信号，将小波阈值去噪原理用于经验模态分解(Empirical Mode Decomposition, EMD)中，提出了EMD阈值去噪方法，用于轴承故障振动信号可以获得较高的信噪比。魏振春等[3]引入双变量改进阈值函数，提出了改进的自适应冗余第二代小波去噪方法，改进方法融合了二者的优点，在强噪声背景下可以很好地保留原信号的特征并有效地去除噪声。苏祖强等[4]针对强噪声、非线性且频率成分复杂的振动信号降噪问题，提出了基于小波包分解和主流形识别的非线性降噪方法，该方法具有良好的非线性降噪能力。周祥鑫等[5]研究了基于小波阈值的高速道岔振动信号降噪方法，并详细讨论了降噪过程中小波基、分解层数、阈值准则、阈值函数等参数的选择。李红延等[6]对比分析了若干不同小波阈值去噪算法，在经典小波阈值去噪算法的基础上改进了阈值函数，提出了新的小波自适应阈值去噪算法，更好地抑制了噪声污染和保持信号细节。除了小波去噪方法，专家学者还研究了众多其他方法，比如付海燕等[7]提出了利用时域同步平均(Time Synchronous Averaging, TSA)技术去除直升机传动系统振动信号噪声，能够有效地去除噪声和无关信号；周晓峰等[8]为了消除旋转机械振动信号中不同类型的噪声，提出了基于虚拟信号的多级独立分量分析的消噪方法，可以得到很好的消噪效果，有效提高了信噪比；隋文涛等[9]将图像处理的总变差降噪方法引入振动信号降噪，用于滚动轴承振动信号的降噪处理等。

在实践中，小波变换和其他传统去噪方法都存在着一个问题，即信号去噪不可避免地模糊了它的细节部分(如冲击和边界等)，而冲击、边界等信号细节部分包含了非常重要的故障特征信息，这一点在强噪声背景信号中尤为严重。因此，信号去噪与保留信号细节特征是一对矛盾，有必要研究既能去噪又能保留信号细节等小尺度特征的方法。

偏微分方程(Partial Differential Equation, PDE)是一种新颖的图像处理方法[10-16]，它利用图像是分段光滑的二元函数这一重要信息，以图像边缘为边界，采用分段连续的函数逼近真实图像，抑制噪声。PDE在去噪的同时可以保留图像的边缘和轮廓等小尺度特征。目前PDE在机械振动信号去噪中的研究还极少[17-19]。在PDE理论中，Perona和Malik提出的Perona-Malik模型是一种典型的非线性各向异性扩散滤波模型，已在图像去噪领域得到了广泛深入的研究和应用，当然它也存在着易受噪声干扰而致边界模糊、鲁棒性差等不足，已有部分学者致力于改进Perona-Malik算法。考虑到小波去噪算法具有一定的抗噪声能力，拟构造一种新的小波变换模扩散系数并引入Perona-Malik非线性各向异性扩散滤波模型，从而综合小波去噪算法和Perona-Malik扩散滤波模型的长处，提出一种改进Perona-Malik模型用于强噪声背景机械振动信号降噪，改进算法兼顾了信号降噪和保留信号细节特征，去噪效果更好。

1 Perona-Malik模型基本理论

Perona-Malik模型是最具代表性、应用也最广泛的非线性各向异性扩散滤波模型之一，它是基于运动的观点来降噪，其基本模型为

(1)

常用的扩散系数为

(2)

(3)

本文采用扩散系数式(2)。

2 基于小波变换模的改进Perona-Malik模型

小波变换是一种非线性、非平稳信号的时频分析方法，是最为重要的信号去噪方法之一，小波变换模反映了信号的幅值变化，并具有一定的抗噪声能力。因此，考虑利用小波变换模替代梯度模用于检测信号的边缘。

首先，分析小波阈值去噪方法和Perona-Malik滤波模型之间的内在联系，其次，构造基于小波变换模的扩散系数并改进Perona-Malik滤波模型。

2.1 小波变换与非线性各向异性扩散的关系

小波阈值去噪方法是非常重要的小波去噪方法之一，它是通过含噪信号小波分解，利用软阈值或硬阈值抑制小波系数，在保持小波系数正负性(可为0)不变的条件下，使小波系数的绝对值比原小波系数的绝对值小，从而有效地去除噪声。

设W表示离散小波变换，W-1表示离散小波逆变换，Sλ表示阈值函数并且满足：x≥0⟹Sλ(x)≥0，Sλ(-x)=-Sλ(x)，|Sλ(x)|≤x，其中λ是阈值门限。

设t=0时刻原信号为u(x,0)，t=1时刻信号为u(x,1)，则原始信号u(x,0)的小波阈值收缩过程可以表示为

W-1g(|Wu(x,0)|)Wu(x,0)

(4)

其中，令g(|x|)=Sλ(x)-I(x)=(Sλ-I)(x)。

由此可得

(5)

式中：|Wu(x,t)|表示信号小波变换模，反映了信号u(x,t)在x处的幅值变化。在幅值变化平缓处，|Wu(x,t)|的值较小；在边缘处，|Wu(x,t)|的值较大，而且信号的奇异性越强，|Wu(x,t)|的值越大。因此，小波变换模正好符合非线性各向异性扩散滤波边缘检测的要求，这也说明小波阈值去噪方法与非线性各向异性扩散滤波方法之间确实存在着非常密切的内在联系。

2.2 改进Perona-Malik模型

因此，改进的一维Perona-Malik扩散滤波模型为

(6)

2.3 改进Perona-Malik模型的滤波性能

在改进Perona-Malik扩散滤波模型中，扩散系数g(|Wu(x,t)|)用于控制平滑速度：当信号位于幅值变化平缓的区域x时，|Wu(x,t)|的值相对较小，g(|Wu|)的值相对较大，此时实行强扩散，这对于去除孤立噪声特别有效；当信号位于边缘x处，|Wu(x,t)|取得局部极大值，从而g(|Wu|)的值相对较小，此时实行弱扩散以保护重要信息。

3 实验分析

3.1 算法比较

利用仿真信号比较小波阈值去噪算法、Perona-Malik扩散滤波模型、改进Perona-Malik扩散滤波模型的去噪效果，并用信噪比(Signal to Noise Ratio, SNR)评价各算法的去噪效果。若信噪比SNR越大，则算法的去噪效果越好。

假设滚动轴承外圈单点损伤故障振动仿真信号为

(7)

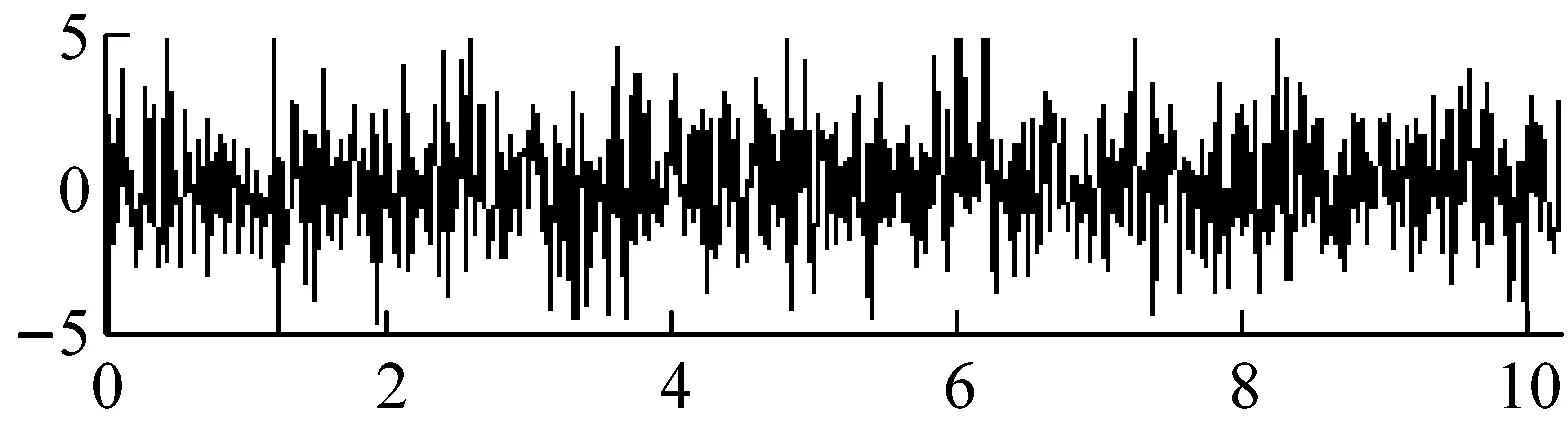
其中，衰减振动的固有频率fn=3 000 Hz，固有振动角频率ωn=2πfn，位移常数y0=5，阻尼系数ξ=0.1，采样频率fs=12 000 Hz，采样点数1 024，如图1(a)所示。

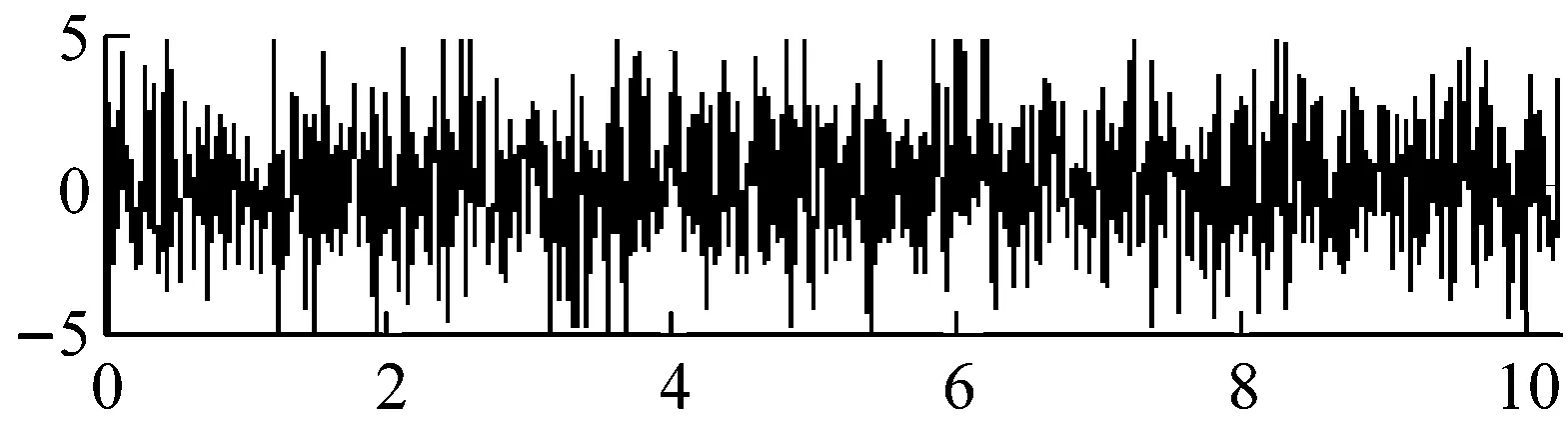
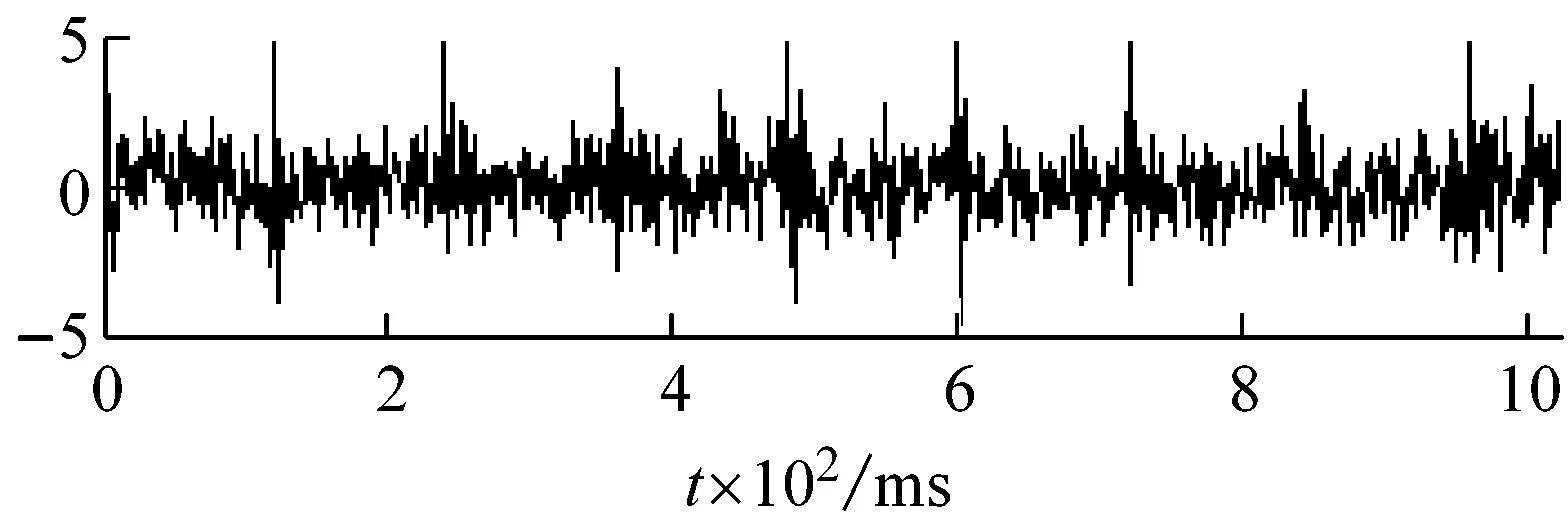
在仿真故障信号(即原始纯净信号)上分别加上不同SNR噪声强度(单位为dB)的Gaussian白噪声即为待分析的含噪信号，如图1(b)(图中SNR=-10 dB)所示。

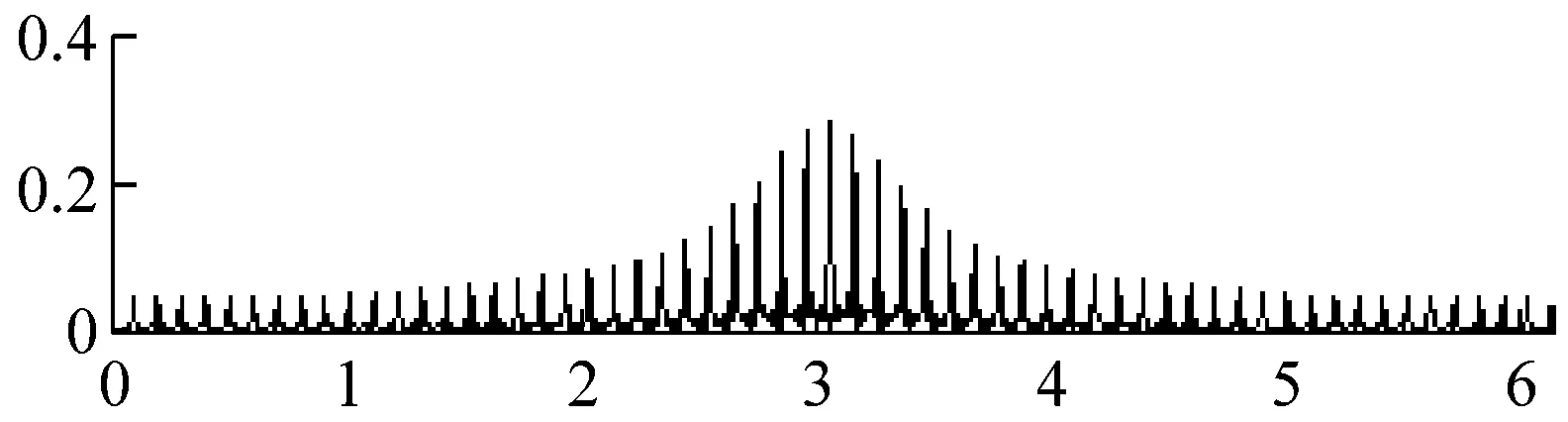
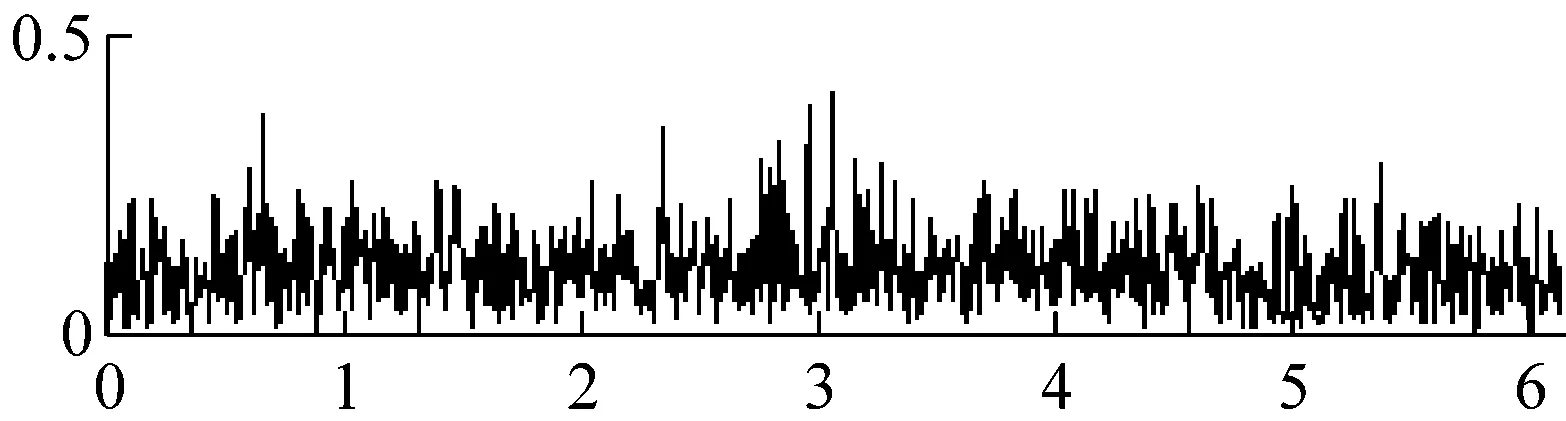
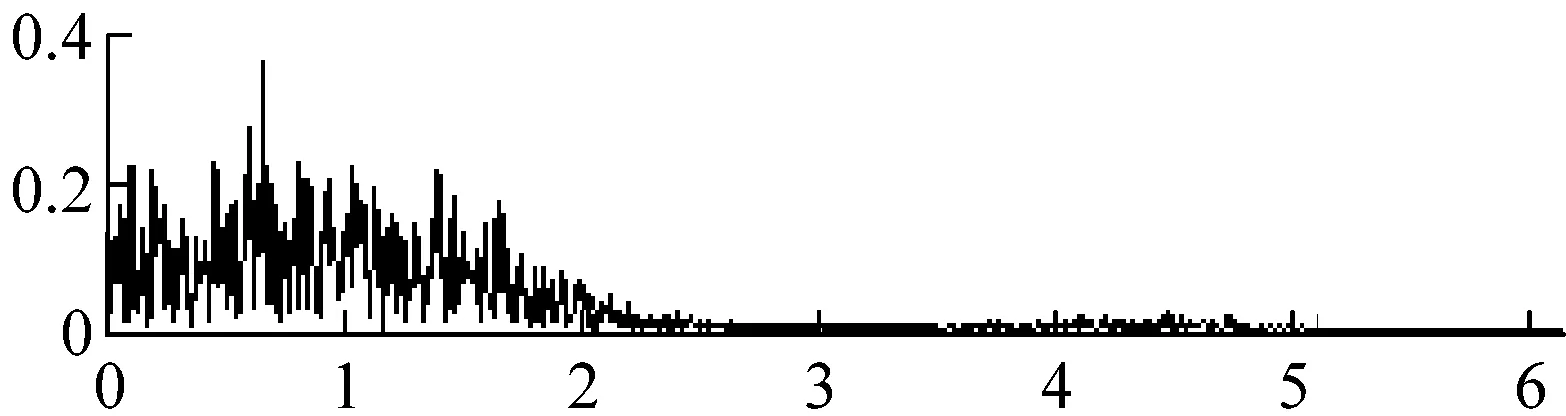
比较小波硬阈值去噪、小波软阈值去噪、Perona-Malik扩散滤波模型、改进Perona-Malik扩散滤波模型的去噪效果，如图1和表1所示。其中，小波阈值去噪的基本参数为：小波基为”sym4”，小波分解层数为2，阈值分别为Stein无偏似然估计阈值(rigrsure规则)、通用阈值(sqtwolog规则)、启发式阈值(heursure规则)、极大极小阈值(minimaxi规则)；Perona-Malik模型的梯度阈值参数k=20，迭代次数如表1所示。

(a)

(f)

(b)

(g)

(c)

(h)

(d)

(i)

(e)

(j)图1 仿真信号去噪Fig.1 Simulation signal denoising表1 仿真信号去噪的SNRTab.1 SNR of simulation signal denoising

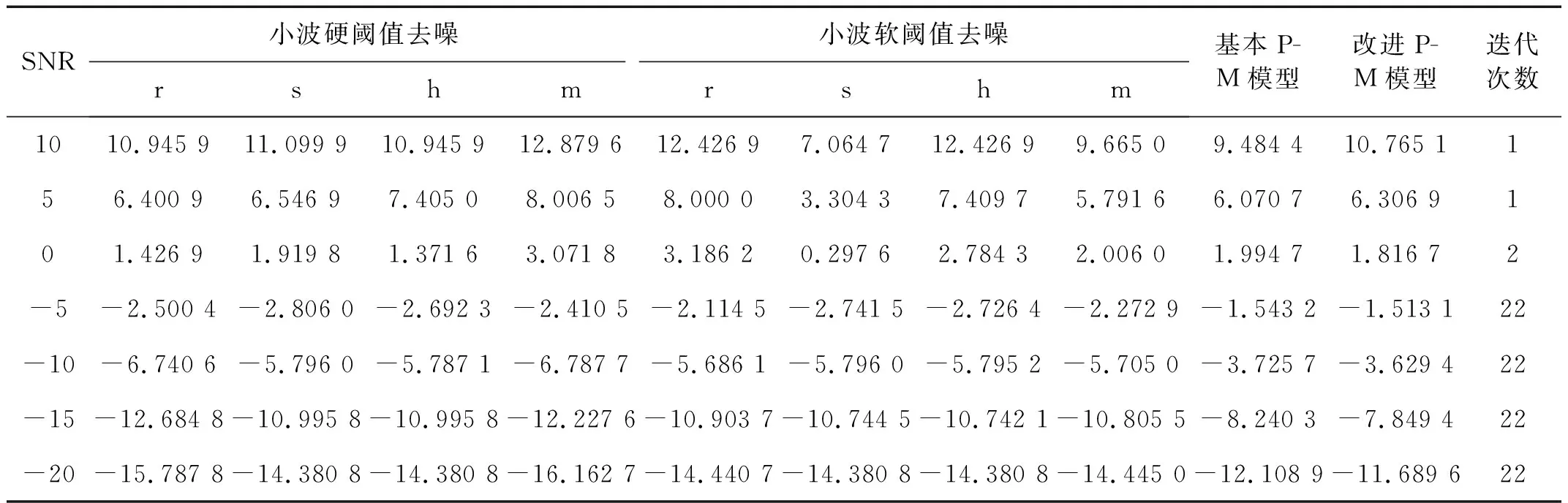
SNR小波硬阈值去噪小波软阈值去噪rshmrshm基本P-M模型改进P-M模型迭代次数1010.945 911.099 910.945 912.879 612.426 97.064 712.426 99.665 09.484 410.765 1156.400 96.546 97.405 08.006 58.000 03.304 37.409 75.791 66.070 76.306 9101.426 91.919 81.371 63.071 83.186 20.297 62.784 32.006 01.994 71.816 72-5-2.500 4-2.806 0-2.692 3-2.410 5-2.114 5-2.741 5-2.726 4-2.272 9-1.543 2-1.513 122-10-6.740 6-5.796 0-5.787 1-6.787 7-5.686 1-5.796 0-5.795 2-5.705 0-3.725 7-3.629 422-15-12.684 8-10.995 8-10.995 8-12.227 6-10.903 7-10.744 5-10.742 1-10.805 5-8.240 3-7.849 422-20-15.787 8-14.380 8-14.380 8-16.162 7-14.440 7-14.380 8-14.380 8-14.445 0-12.108 9-11.689 622

根据图1和表1可得结论：①小波硬阈值去噪、小波软阈值去噪、Perona-Malik模型、改进Perona-Malik模型均可去除信号噪声，小波(硬/软)阈值去噪平滑了部分有用信号细节特征，Perona-Malik模型及其改进模型则保留了信号细节特征；②在弱噪声(即SNR=10、5、0)时，四种算法的去噪效果差别不大，相比Perona-Malik模型及其改进模型，小波(硬、软)阈值去噪算法效果稍好；③在强噪声(即SNR=-5、-10、-15、-20)时，Perona-Malik模型的去噪效果明显强于小波(硬/软)阈值去噪算法，改进Perona-Malik模型又强于基本Perona-Malik模型，改进算法使信噪比平均提高了约3 dB；④相比基本Perona-Malik模型，改进Perona-Malik模型利用小波变换模替代梯度模来检测边缘，其抗噪声干扰能力更强，规避了基本Perona-Malik模型线性低通滤波导致的边界模糊等问题。因此，改进Perona-Malik模型的去噪效果更好。

综上所述，相比小波阈值去噪等传统去噪算法和基本Perona-Malik模型，改进Perona-Malik模型更适用于强噪声信号去噪。

除了Gaussian白噪声，改进算法用于其他类型噪声(如脉冲噪声、高频窄带干扰)，其降噪性能也优于小波阈值去噪算法和基本Perona-Mailik模型；并且除了加性噪声，作者还研究了改进算法用于乘性噪声降噪，其降噪效果也较好，如表2所示。

表2 改进算法用于其他噪声的SNR(-10 dB)Tab.2 Modified algorithm SNR for other noises (-10 dB)

3.2 实测振动信号降噪

为进一步验证改进Perona-Malik模型滤波算法的有效性和实用性，用某热电厂驱动电机端轴承振动信号来去除噪声，轴承参数如表3所示，轴承检测如图2所示。图3(a)所示信号为轴承外圈故障振动信号，其中，采样频率为12 kHz，轴转速为1 719 r/min。

表3 轴承结构参数Tab.3 Bearing structural parameters

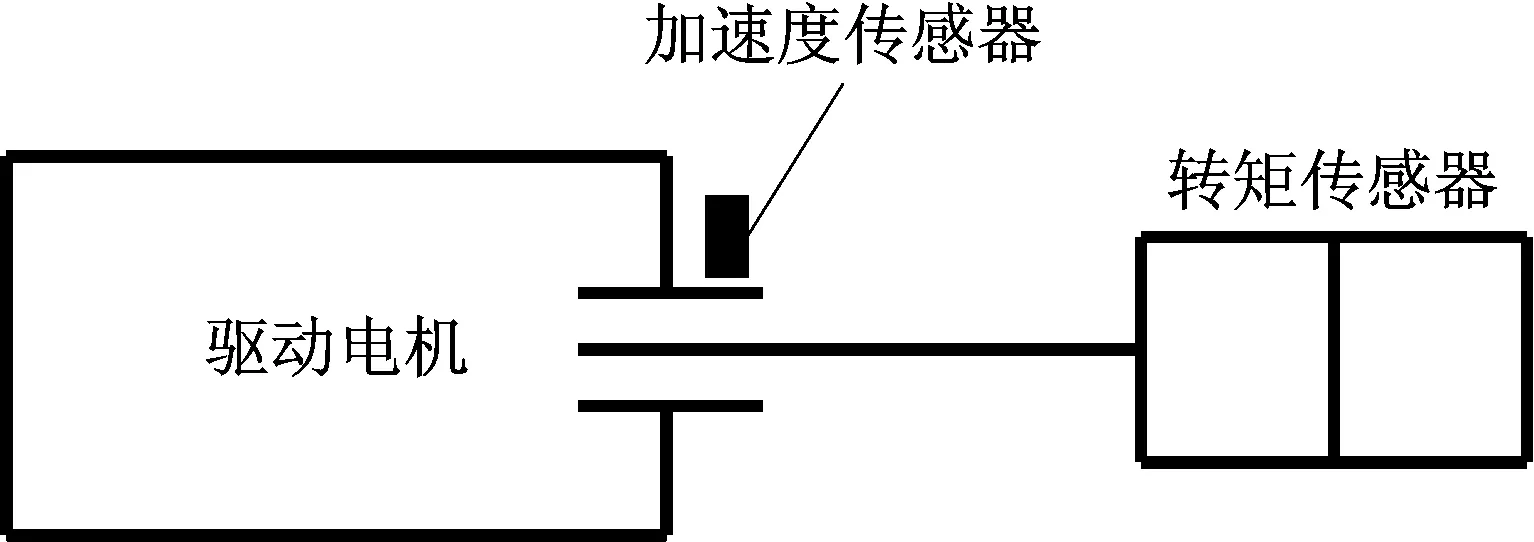
图2 轴承检测Fig.2 Bearing detecting

图3(a)所示为实测轴承振动信号及其幅值谱，图3(b)所示为利用改进Perona-Malik模型用于实测含噪信号后得到的去噪信号及其幅值谱，其中，扩散系数梯度阈值参数k=20，迭代次数为1。由图3可知，只需迭代1次，改进Perona-Malik模型就较好去除了含噪信号中的噪声，突出了它的特征频率(外圈故障特征频率为103 Hz)及其倍频，从而便于后续强噪声背景微弱故障特征提取，因此，改进算法是可以应用于实际的机械振动信号降噪的，并且优于传统的信号降噪算法。

(a)

(c)

(b)

(d)图3 实测信号去噪Fig.3 Measured signal denoising

4 结 论

在基本Perona-Malik模型基础上，引入小波变换模替代梯度摸构建改进的扩散系数，提出了基于小波变换模改进Perona-Malik模型强噪声背景信号滤波算法。数值仿真分析和实测实验表明，相比小波变换等传统去噪方法和基本Perona-Malik模型，改进Perona-Malik模型滤波算法既能有效地去除噪声，又能较好地保留信号的细节特征，改进算法抗孤立噪声干扰能力强，去噪之后信号畸变小。当然，改进模型还有待进一步深入讨论和研究，比如改进算法中如何选取小波函数等。