平台运动与管内流动联合作用下悬垂立管动力响应特性研究

吴天昊， 付世晓， 任桐鑫, 何 玥

(1. 上海交通大学 海洋工程国家重点实验室，上海 200240； 2. 高新船舶与深海开发装备协同创新中心，上海 200240；3. 上海交通大学 船舶海洋与建筑工程学院，上海 200240)

近年来，大管径悬垂立管在海洋工程中得到了广泛的应用。在深海采矿工程中，输送系统主要由大管径的弹性软管组成，它连接水面母船与海底基础，管中是矿物泥水的两相流，其长度可达数千米，从工程角度考虑，该管道需要满足输运能力、输运效率、安全性、稳定性等多方面的要求。此外，在海洋温差能发电(OTEC)中，悬垂立管不仅要保证具有足够的保温性能，其在深海环境中的安全性能也是制约温差发电实现的难题之一。另外随着世界各国对海洋油气资源的开发不断深入，在FLNG进行深海油气开采时，也采用了竖直的大管径悬垂立管抽取深海中的冷水将天然气进行液化，进而提高生产效率和经济效益。上述三种悬垂立管作业时，立管顶端均悬挂于浮式生产平台或船体，在顶端平台运动，海流和管内流动的共同作用下，悬垂立管极易产生涡激振动，进而引发立管的疲劳累积，对系统的安全性造成不利影响，特别是深水立管发生破损时后果更是无法估量。基于以上背景，悬垂立管成为近几十年许多学者的研究热点。

目前，学者们对于立管涡激振动的研究主要针对海洋中的背景洋流，并将其简化为流向不随时间变化的均匀流或者剪切流[1-8]。而现实中的海洋平台由于风、浪、流的作用会在一定区域内产生往复的运动，这种往复运动带动立管运动，并与其周围水质点之间形成等效的相对振荡来流。这种振荡来流也极易在立管尾部引起稳定的漩涡脱落，从而进一步导致升力的周期性变化。因此，等效振荡流场更能反映出真实的工程情况,称为平台运动诱发的VIV。学者们对于平台运动作用下立管的响应做了细致研究，研究表明平台运动不仅会导致柔性立管顺流向(IL)的全局响应，还可能引起柔性立管横流向(CF)的涡激振动。平台运动引起的VIV有很强的分时特性。KC数和IL法向速度是影响平台运动诱导下立管VIV的主要因素[9-13]。

国内外学者在内流作用对立管动力响应的影响上也做了许多研究。Chen[14]分析了均匀弯曲输流管道的动力特性，认为内流作用会产生两种力: 科氏力(Coriolis force)和离心力(Centrifugal force)。学者们发现随着内流速度的增加，立管的固有频率减小[15-17]。Chang等[18-19]解释了原因，研究指出，内流实际上通过对减小局部轴力项从而减小立管的固有频率。

针对 “平台运动和内流共同作用下会诱发怎样的立管涡激振动？”这一问题，当前工业界、学术界还没有给出定性和定量的结论。

为研究平台运动与内流联合作用下的大尺度悬垂立管涡激振动响应特性，本文进行了模型试验，模型试验内容包含预试验，不含顶端柔性抽水管试验以及正式试验，工况包括内流速度分别为0 m/s,0.4 m/s,0.8 m/s，平台顶端简谐、随机运动，整体工况达到200余项。

本文重点研究平台运动以及内流作用下的悬垂立管运动响应特性，研究包括以下两个方面：① 研究内流对于悬垂立管动力响应特性的影响；② 研究KC数对于悬垂立管涡激振动响应特性的影响。

1 悬垂立管模型试验

试验模型的安装简图如图1(a)所示。立管模型全长30 m, 外径0.163 m，竖直放置于深水池的深井中。立管模型详细参数如表1所示。如图1(b)试验装置细节图所示，试验中采用二自由度强迫运动装置带动立管顶部运动以模拟平台运动(水平运动、竖直运动)的作用。立管模型的顶部以铰接的方式与强迫运动装置相连，底端自由，装有16 kg配重。

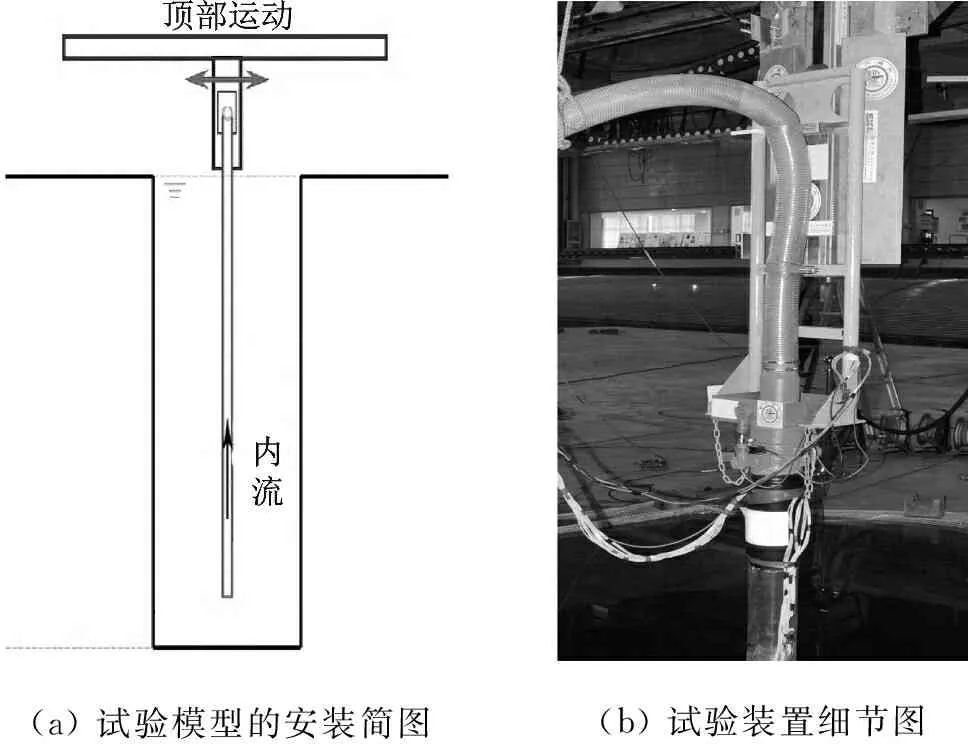
(a) 试验模型的安装简图(b) 试验装置细节图

图1 立管模型试验图 Fig.1 Riser model表1 立管模型主要物理参数Tab.1 Physical parameters of the riser model

为测量立管的动态响应，如图2所示，沿立管模型长度方向选取16个截面，每个截面布置4个(A，B，C，D)光纤光栅应变传感器，测量CF方向和IL方向的动态应变。其中，B、D测量IL方向的应变，A、C测量CF方向的应变响应，如图2所示。选取的第一个截面位于水面下0.96 m，第二个截面位于第一个下方1 m处，其余的14个截面以相同的间距(2 m)自上而下均匀地布置在模型上。同时，试验中采用两个单分力仪测量立管顶端的实时轴向张力。

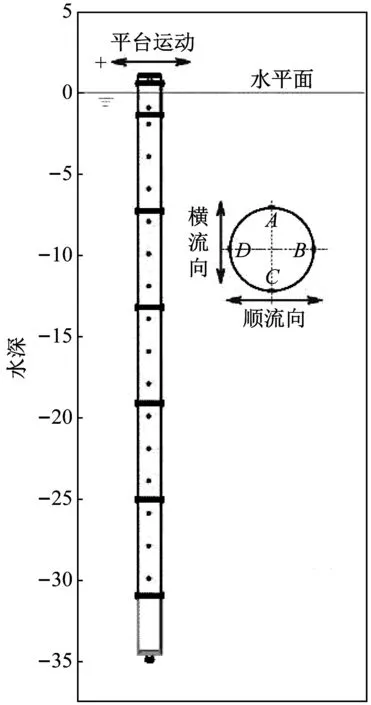
图2 抽水立管模型参数和光纤光栅传感器布置Fig.2 WIR model configuration and strain sensor layout

本文研究平台的水平运动以及内流对立管动力响应的影响，因此选取4个水平正弦运动的工况，如表2所示。

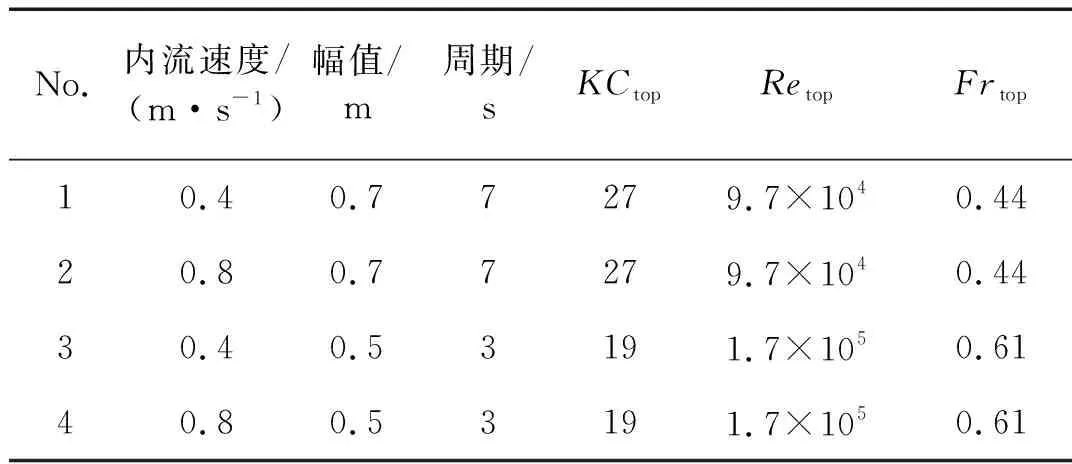
表2 本文分析的工况Tab.2 4 cases in this paper

Aim为平台水平运动振幅(m)，Tim为平台水平运动周期(s)，Vim为平台运动速度幅值，KCtop为悬垂立管顶部的KC数，其计算公式为

(1)

式中：D为悬垂立管的外径(m)。

Retop为悬垂立管顶部的雷诺数，其计算公式为

(2)

式中：ν是水的运动黏性系数，其值为1×10-6m2/s。

Frtop为悬垂立管顶部的傅汝德数，其计算公式为

(3)

式中：g是重力加速度，其值为9.8 kg/N。

2 数据分析

2.1 数据预处理

在本试验中，由于立管模型自重的作用，立管模型会承受轴向张力，轴向张力会使立管表面产生轴向应变。当立管发生涡激振动时，由于立管的周期振动，立管的轴向张力也是周期振动的，使得测量的应变信号包括两个部分：由张力产生的轴向应变以及由涡激振动产生的轴向应变。由预张力产生的弯曲应变必须加以消除。图2中，CF1和CF2相互对称，因此由涡激振动产生的弯曲应变大小相等，方向相反，而轴向力产生的应变是相同的，那么CF1和CF2处的应变可写为

εA=εVIV-CF+εT,εC=-εVIV-CF+εT

(4)

对上式进行简单的变换，便可得到CF向由涡激振动引起的弯曲应变为

(5)

同理，IL向的弯曲应变为

(6)

2.2 位移响应分析法

得到各测点处弯曲应变的时历数据后，需通过模态分析法得到整根立管各点的位移响应。应用ORCAFLEX软件[20]，计算静水中悬垂立管模型前10阶模态的固有频率如图3所示。由于试验模型完全对称，立管模型IL向和CF向的固有频率完全相同。

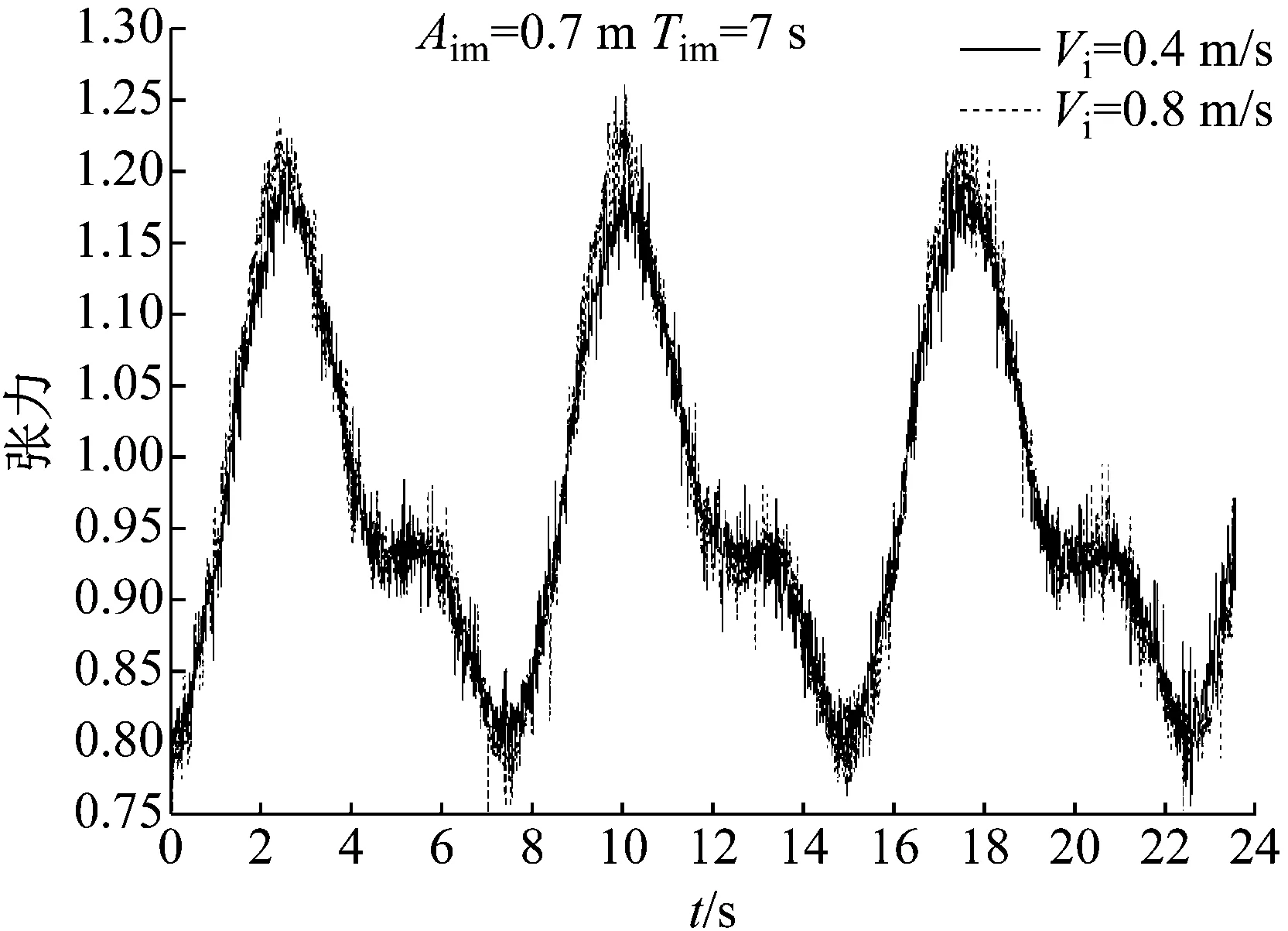
图3 静水中试验模型的前10阶固有频率Fig.3 The first 10 order natural frequency in still water

假设受轴向力作用的立管做小变形的振动，则立管CF向的涡激振动响应可基于模态叠加法写为

(7)

式中：pi(t)表示第i阶模态的位移模态权重；φi(s)表示模型CF向的第i阶位移振型函数；w(t,s)为立管CF向涡激振动位移时历。

根据位移与曲率之间的空间二次导数关系，可以得到曲率κ(t,s)的表达式

(8)

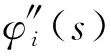
又曲率与弯曲应变间的几何关系式为

ε(t,s)=R·κ(t,s)

(9)

式中：R为立管半径。则可以得到应变的模态叠加表达式为

(10)

对于本文的悬垂立管模型而言，其轴向力沿管长方向呈非线性分布，振型函数不存在理论解，本文考虑了悬垂立管本身材料不同等因素，按照真实试验模型设计，应用ORCAFLEX软件计算固有频率和振型。立管模型在静水中的前6阶CF向归一化位移振型如图4所示。

图4 试验模型静水中前6阶归一化位移振型Fig.4 The first 6 order modal shape

3 结果分析

本文在王俊高等对于悬垂立管动力响应特性基础上，研究悬垂立管顶部张力，顺流向(IL)全局响应，横流向(CF方向)VIV响应特性以及阻力系数分布等问题。主要包括振荡流和内流共同作用下，顶部张力分析，IL向阻力系数，KC数、泻涡频率分布、振荡来流速度，以及CF向VIV响应应变和空、时频特性分析等。

3.1 悬垂立管顶部张力分析

研究指出，内流实际上通过对局部轴力项的影响而改变立管的固有频率。Patel等[21]考虑有内流作用下的内、外压力、内流重力以及内流动力势能对于有效张力的影响，将有内流影响的有效张力定义为下式

Te=Ttw-PiAi+PeAe-ρAinu2

(11)

式中：Te为有效张力；Ttw为壁面真实张力；Pi,Pe为内、外流压力；Ai，Ae为内、外流压力作用面积；ρ为内流流体密度；Ain为管内截面面积；u为内流速度。式中最后一项为内流动力势能对于有效张力的影响项，可以发现内流速度对应为平方项，内流速度增大对导致有效张力减小，但并不依赖于内流方向。

则边界条件为两端铰接的情况下，有内流影响的固有频率可以写为

(12)

式中：E为弹性模量；I为截面惯性矩；ρb为密度；A为梁截面面积。

本文试验中，立管的边界条件为一端铰接一端自由，没有解析解。为了定性描述内流对于悬垂立管固有频率的影响，应用两端铰接边界条件下的解析解公式，可以直观证明内流速度增加会导致悬垂立管固有频率的减小的事实。

试验中，三分力仪置于悬垂立管顶部，可以测得悬垂立管顶部轴向张力，可以视为有效张力Te。如图5所示，为试验中4种工况下，悬垂立管顶部轴向张力与平均轴向张力之比。计算四种工况下，悬垂立管的顶部张力均方差结果，记为σT，如表3所示。可以发现平台运动下悬垂立管的顶部张力是不断变化的，不同内流速度，相同顶端平台运动作用下，悬垂立管顶端张力均方差结果相近，这说明本试验顶部张力受内流速度变化影响不大。相同内流速度，不同顶部平台运动作用下，顶端平台运动幅值为0.7 m，周期为7 s，悬垂立管顶端张力平均值、均方差结果均大于顶端平台运动幅值为0.5 m，3 s的结果，这与悬垂立管受到的阻力和惯性力不同有关。式(11)中，将本试验中两种内流速度结果代入，发现内流速度对于有效张力的影响最大仅为2.8%左右，可以视为内流速度对于悬垂立管的固有频率影响不大。

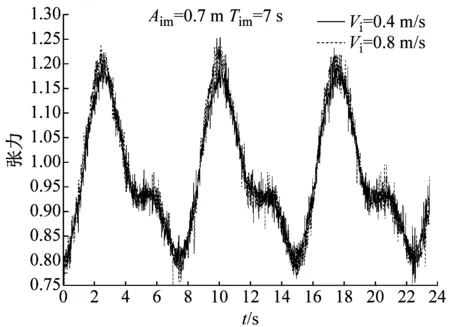
(a) Aim=0.7 m，Tim=7 s

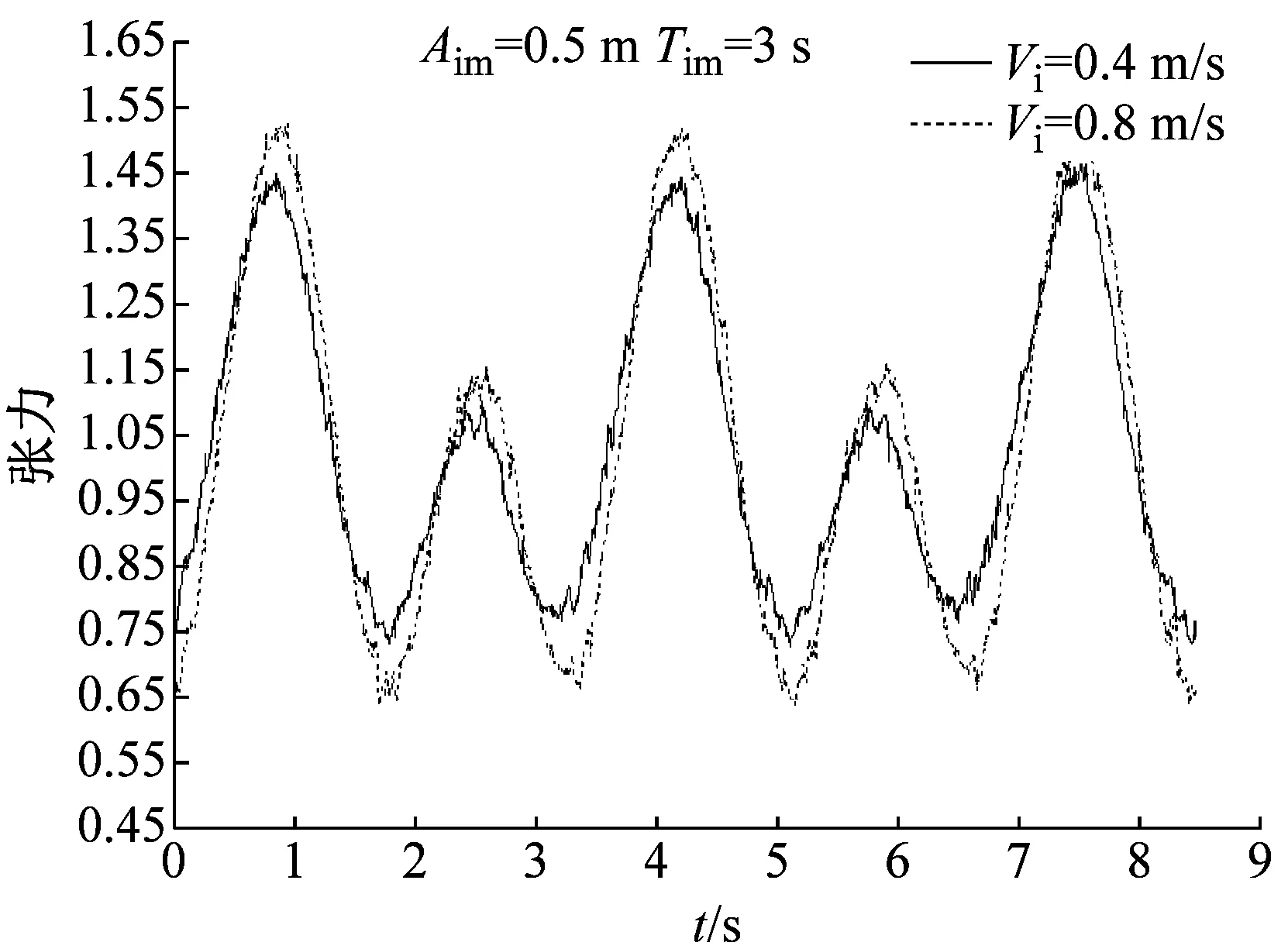
(b) Aim=0.5 m，Tim=3 s

图5 4种工况不同内流速度下悬垂立管顶部轴向张力与平均轴向张力之比

Fig.5 Ratio of top axial tension variation and average axial tension in 4 cases under different internal flow velocity

表3 4种工况下悬垂立管顶部张力的均方差Tab.3 The MSE of top tension of risers in 4 cases

3.2 平台运动以及内流共同作用下的悬垂立管动力响应特性

本节首先研究悬垂立管顺流向面内全局响应特性，包括研究悬垂立管KC数，泻涡频率分布情况以及振荡流场速度变化情况，以及IL向应变响应特性，为研究CF向悬垂立管的涡激振动响应特性提供帮助。悬垂立管CF向应变响应主要由涡激振动引起，而后主要研究悬垂立管在振荡流和管内流动共同作用下的CF向应变响应特性，包括CF向应变RMS值，空间响应频率特性分析，时频特性分析等。

试验中，悬垂立管的16个测点中有部分测点位置处粘贴标识，并用水下摄像机拍摄视频，记录悬垂立管的IL向的位置变化，可以根据悬垂立管直径，以及视频中悬垂立管移动的位置，来判断这一测点位移的幅值An。试验中，水下摄像机位置固定，采样时严格按照每一帧画面进行采样，选取对应测点运动位移的幅值位置，并通过空间位置识别方法较为精确的计算画面中的测点位置变化。通过这种方法，可以求得试验中较为真实的KC数。

王俊高等证明，在没有内流作用下，阻力系数Cd为1.8时最接近试验结果。因此，应用ORCAFLEX软件计算在阻力系数为1.8时，两种工况(Aim=0.7 m,Tim=7 s，Aim=0.5 m,Tim=3 s)悬垂立管两种内流速度作用下IL向位移响应幅值，并计算KC数。如图6(a)和(b)所示，为两种顶部平台运动情况，不同内流速度下，通过ORCAFLEX软件数值模拟的KC数，以及视频位移识别法得到的部分测点的KC数结果。

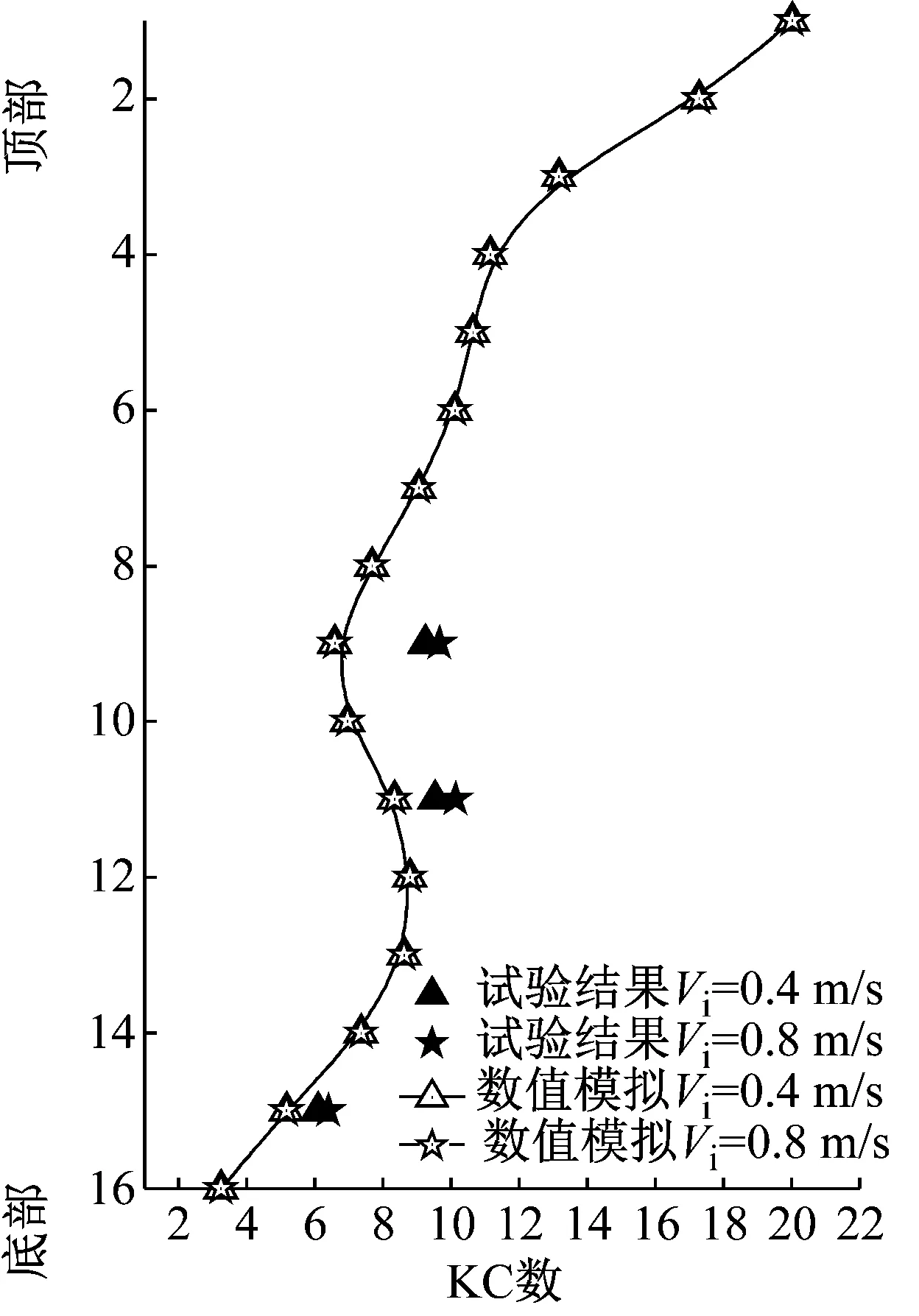
(a) Aim=0.7 m，Tim=7 s

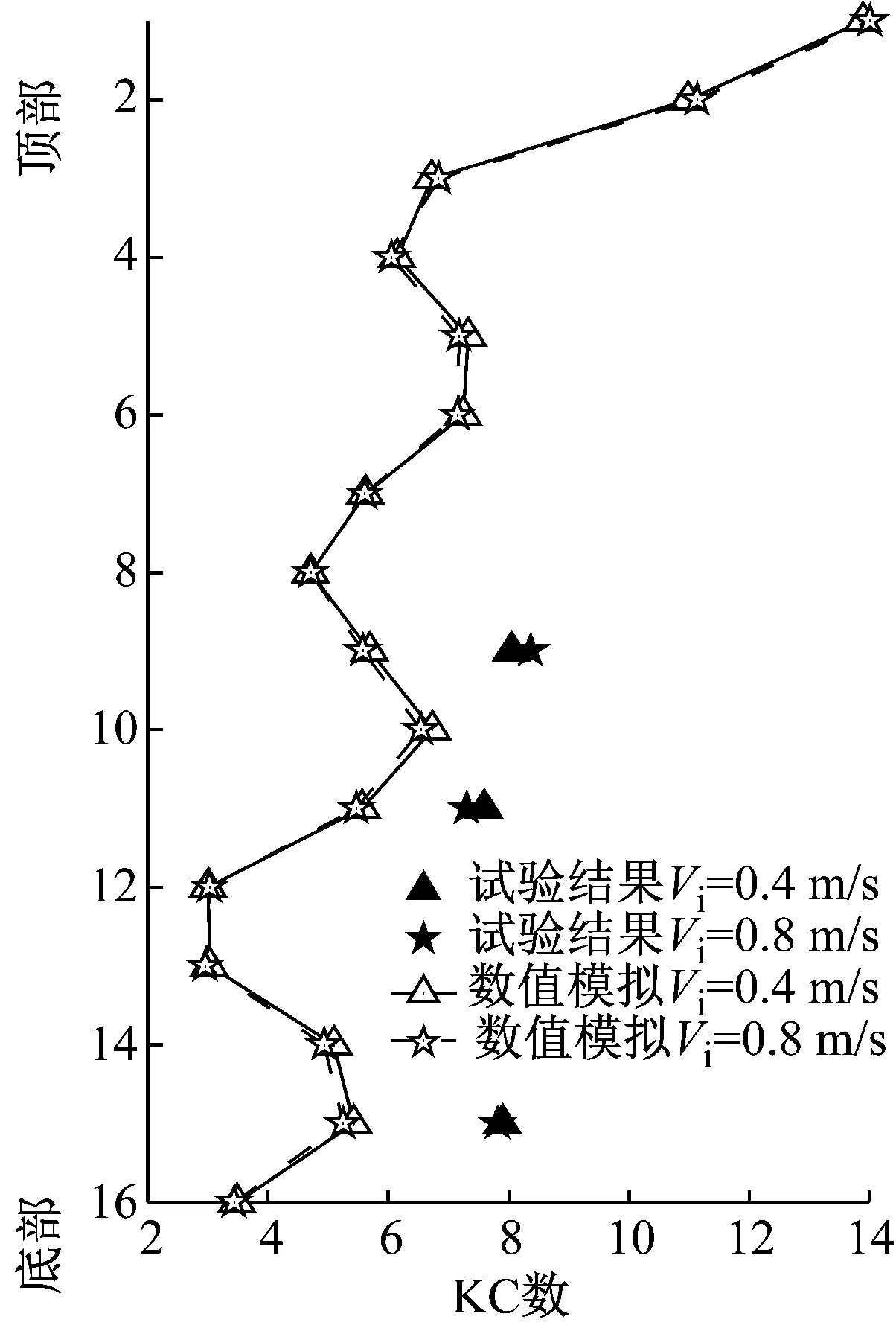
(b) Aim=0.5 m，Tim=3 s

(c) Aim=0.7 m，Tim=7 s

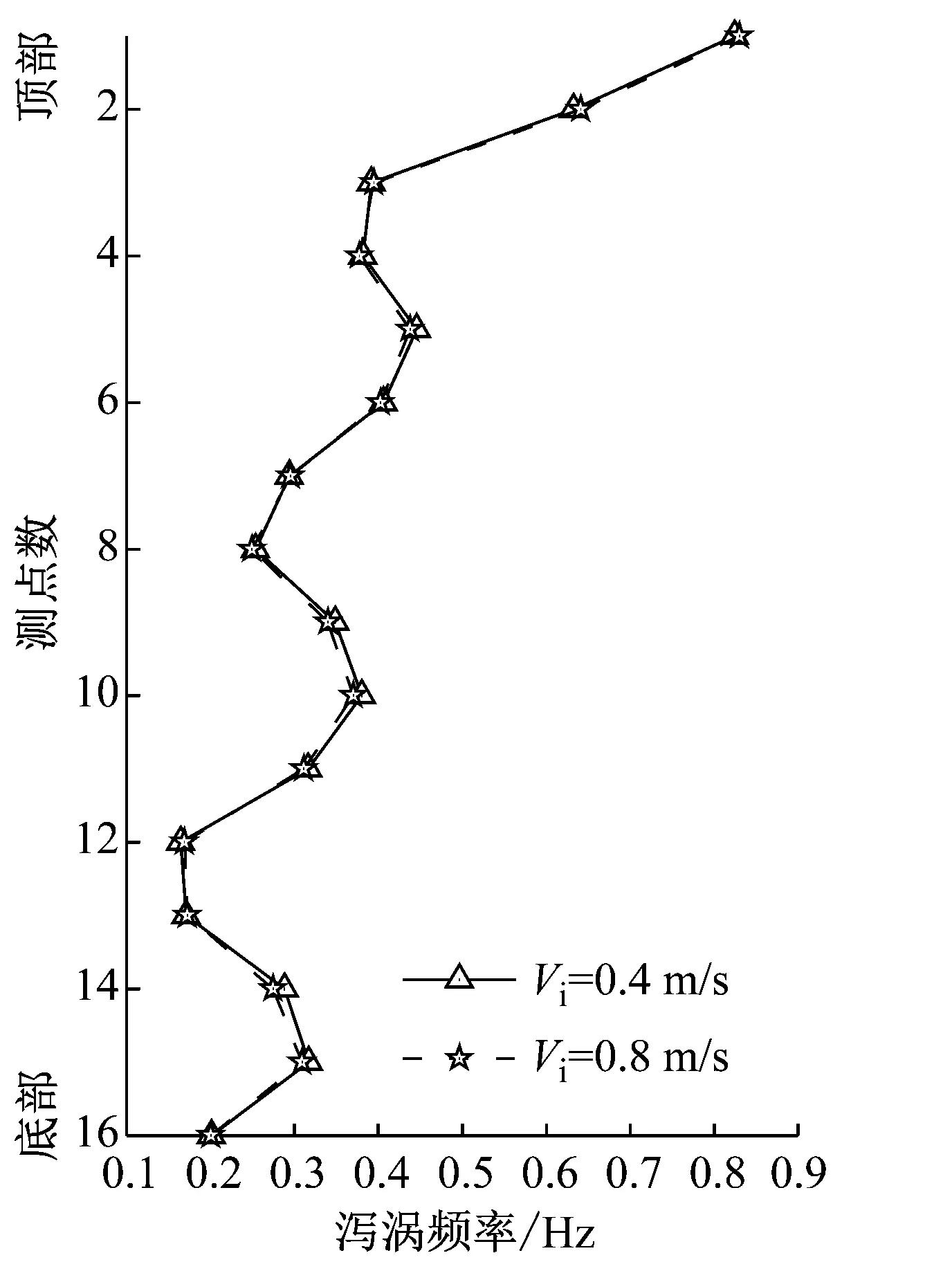
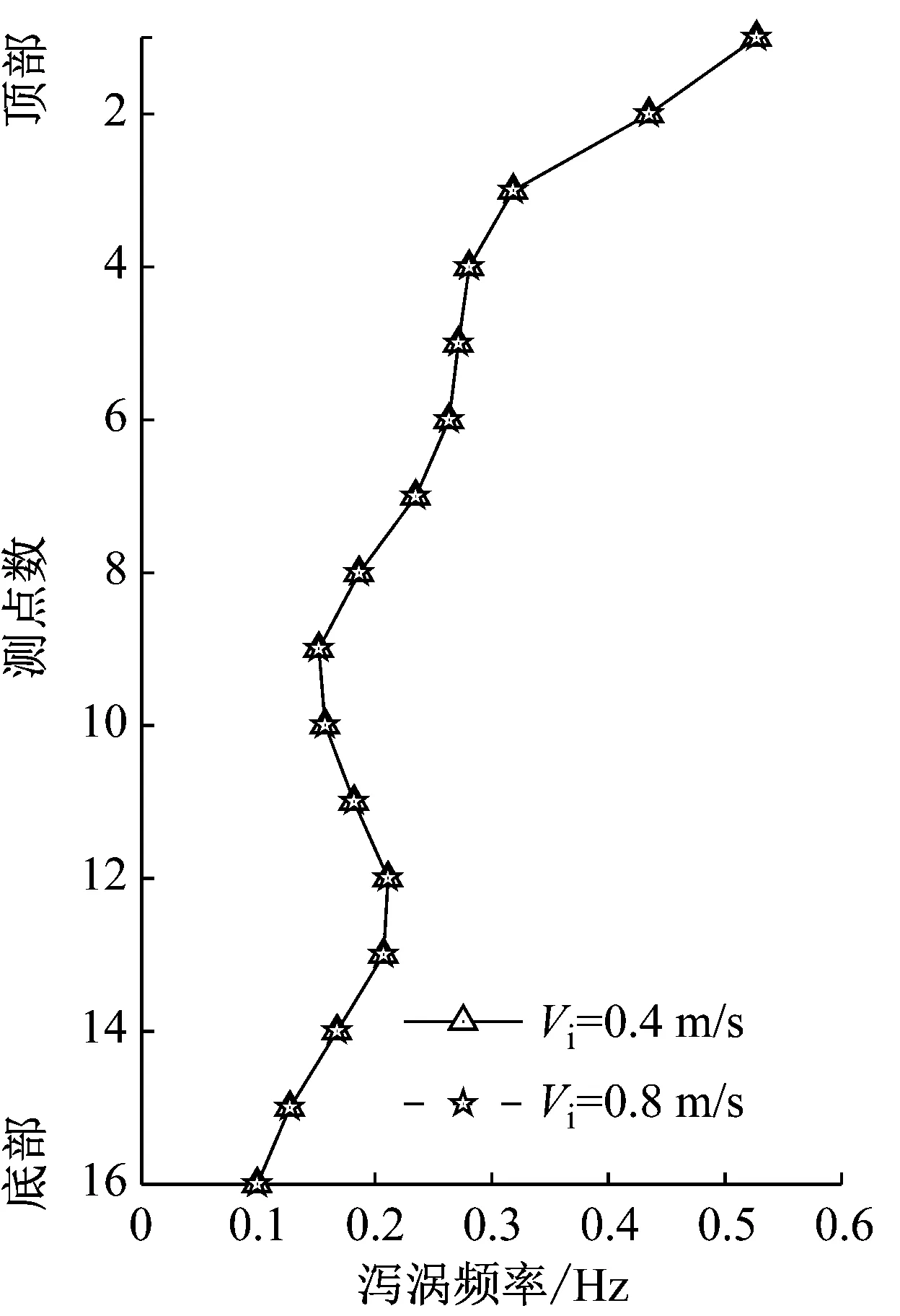
(d) Aim=0.5 m，Tim=3 s图6 KC数和泻涡频率幅值沿管长变化的分布Fig.6 Distribution of KC number and Fst-amp along the length of the riser

在振荡流场中，基于斯托哈尔数关系，瞬时泻涡频率fst(s,t)，以及泻涡频率幅值fst_amp(s)可以由下式表示

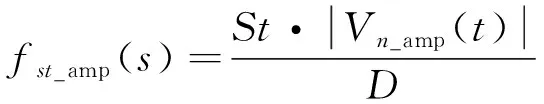
(13)

其中St为斯托哈尔数，设为0.2来初步粗略估计立管泻涡频率范围，D为立管外径，Vn(s,t)为瞬时IL向来流速度，Vn_amp(s)为Vn(s,t)的幅值。

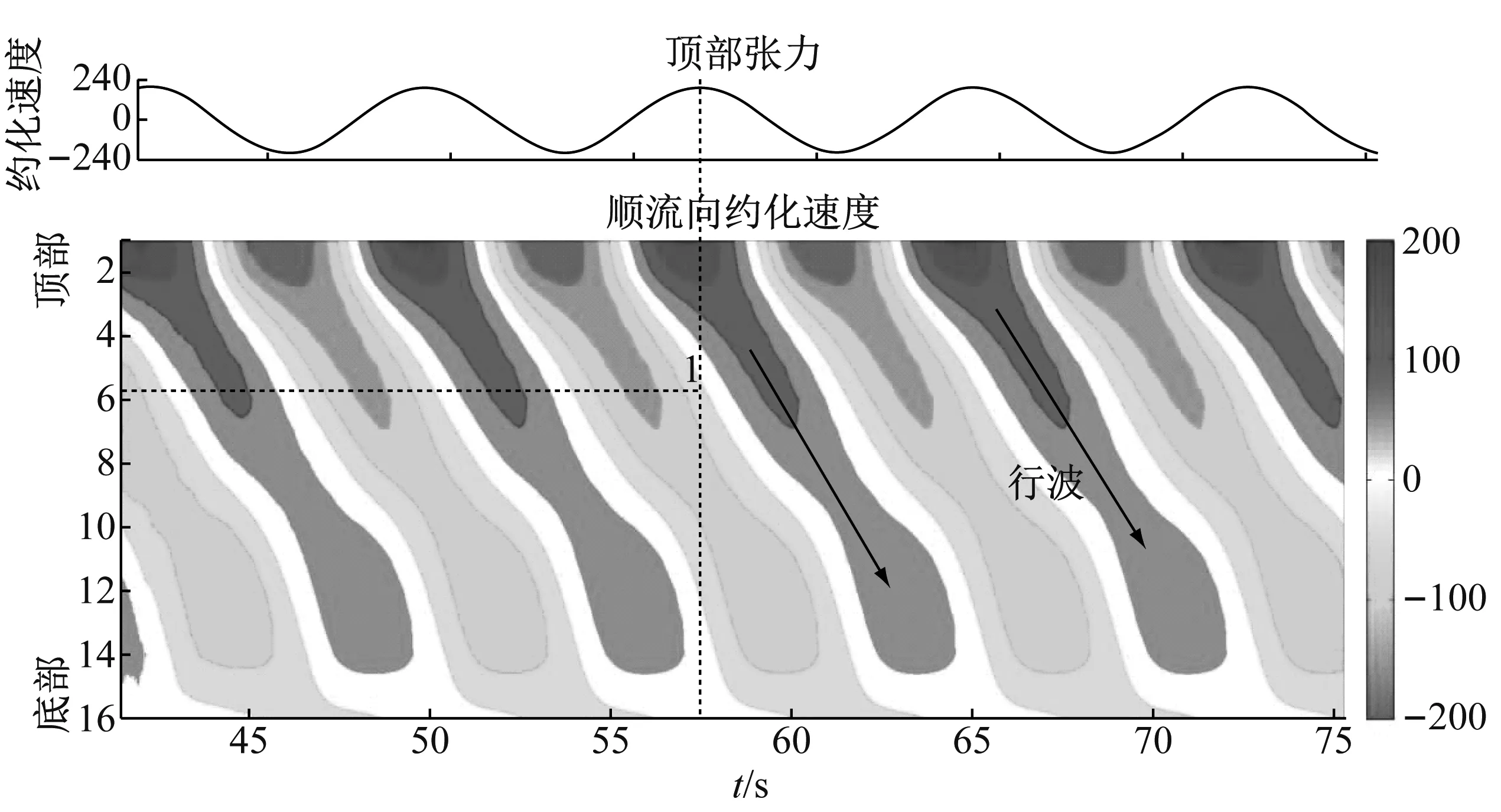
通过ORCAFLEX软件数值模拟IL向流速幅值，并计算泻涡频率幅值，结果如图6(c)和(d)所示。值得一提的是，由于St数取到0.2为估计值，所以对应的泻涡频率并不等于试验中的真实泻涡频率，但是图中可以反映不同工况下，泻涡频率的具体分布情况。立管的IL向法向速度分布也会影响立管的CF向涡激振动响应。研究表明，随时间周期性变化的法向速度会引起间歇性的涡激振动响应[22]。因此，本文需要建立IL向法向速度的分布特性。通过ORCAFLEX模拟发现，两种内流速度下，IL法向速度分布云图相似，如图7(a)和(b)所示为内流速度为0.4 m/s时，两种顶端平台运动的结果。

(a) Aim=0.7 m，Tim=7 s

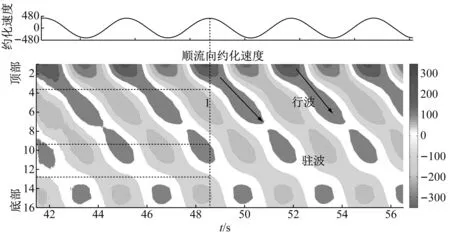
(b) Aim=0.5 m，Tim=3 s图7 IL向法向速度分布图Fig.7 Transient IL direction normal velocity distribution

如图6(a)和(b)所示，视频位移识别法获得的3个测点KC数大于ORCAFLEX数值模拟的结果，这是因为阻力系数会沿管长方向发生变化，并非固定值，三个测点的变化趋势和数值模拟的结果相似，说明数值模拟结果的可靠性。观察数值模拟以及视频位移分析法结果，不同内流速度下，KC数变化均不大，说明本试验内流流速区间对于KC数影响不大，可以忽略。如图6(c)和(d)所示，同种顶部平台运动情况不同内流速度下，泻涡频率整体分布趋势较为相似，即本试验内流流速区间对于泻涡频率幅值影响不大。纵观图6(a)～6(d)，各点KC数幅值、泻涡频率幅值呈现类似“波浪状”分布，但整体呈现减小趋势。此外，对于A=0.7 m,T=7 s的工况，顶部运动幅值较大，KC数相对较大，但是由于顶部运动周期较长，所以影响了速度项，因此各点泻涡频率的幅值偏小。

纵观图7，IL向法向速度呈现出明显的行波特征，在某些测点会出现驻波特性。以图7(b)为例，当t=48.1 s时，立管的IL向法向速度沿着管长方向有不同的流向攻角。下面两幅图标出了某一时刻当顶端运动速度达到最大时，沿管长分布的速度情况，其中图7(a)工况均出现了一次速度方向变化，伴有行波特性，图7(b)工况出现了三次速度方向变化，且伴有行波特性以及驻波特性。这说明，悬垂立管在顶端平台简谐运动带动下，与静水形成了一种复杂的双向剪切流场，这样的双向剪切流场是否会产生涡激振动，如果会产生涡激振动，那么其涡激振动响应特性又是如何？后文将给出详细研究。

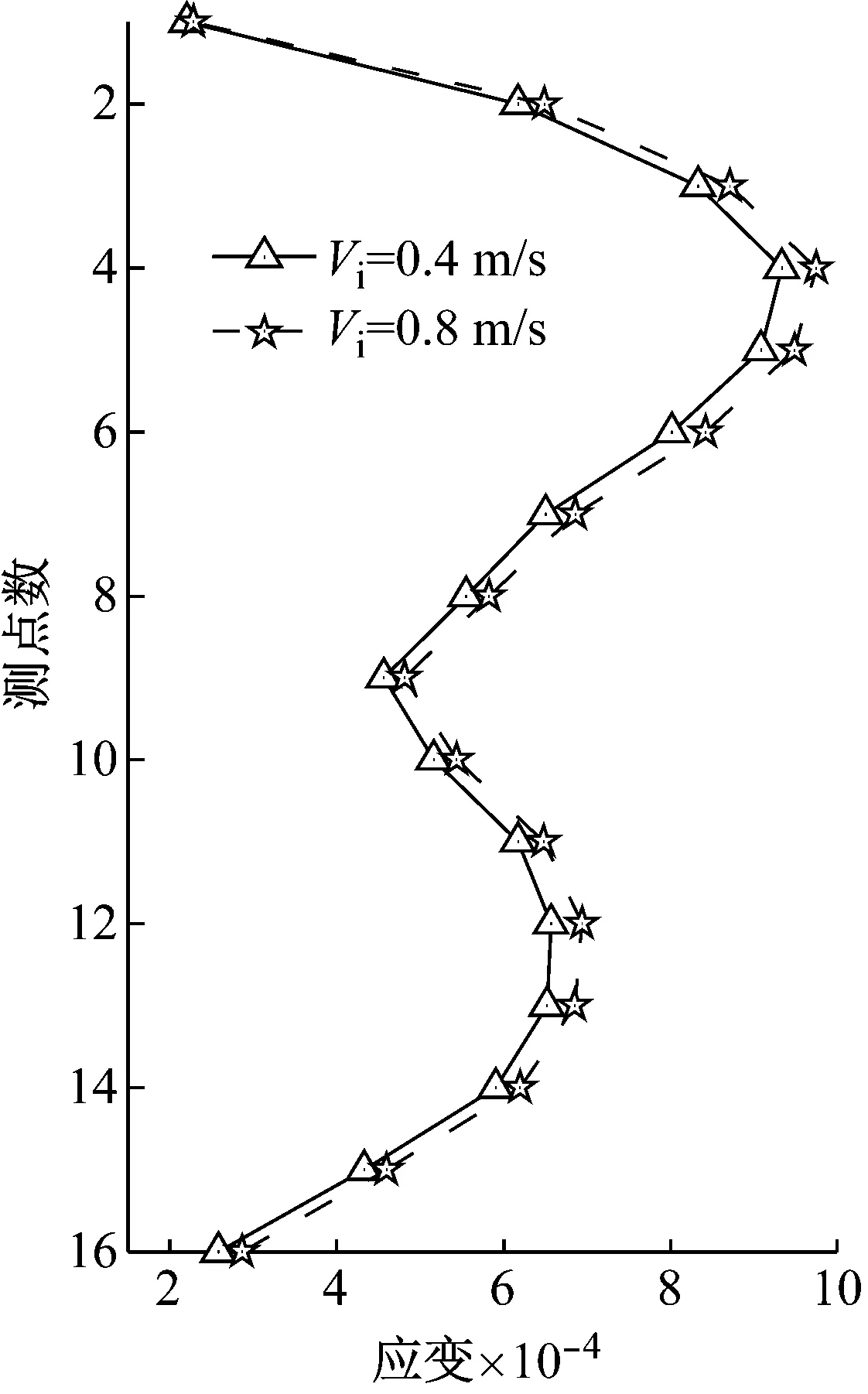
将4种试验工况下16个测点的IL方向应变RMS值结果进行统计，如图8所示，分别给出了两种顶端平台运动幅值和周期下，IL方向不同内流速度对应的应变RMS值。综合分析图8，可以发现悬垂立管的整体主导模态和顶部平台运动频率相同，顶端平台运动幅值和周期为0.7 m, 7 s时，悬垂立管IL向呈现3阶主导模态，顶端平台运动幅值和周期为0.5 m, 3 s时，悬垂立管IL向呈现5阶主导模态。在顶端平台运动情况相同，内流速度不同时，悬垂立管IL向应变响应RMS值略微不同，这很可能是由于CF向VIV涡激振动响应特性不同， IL向阻力系数发生改变导致的[23]。

(a) Aim=0.7 m，Tim=7 s

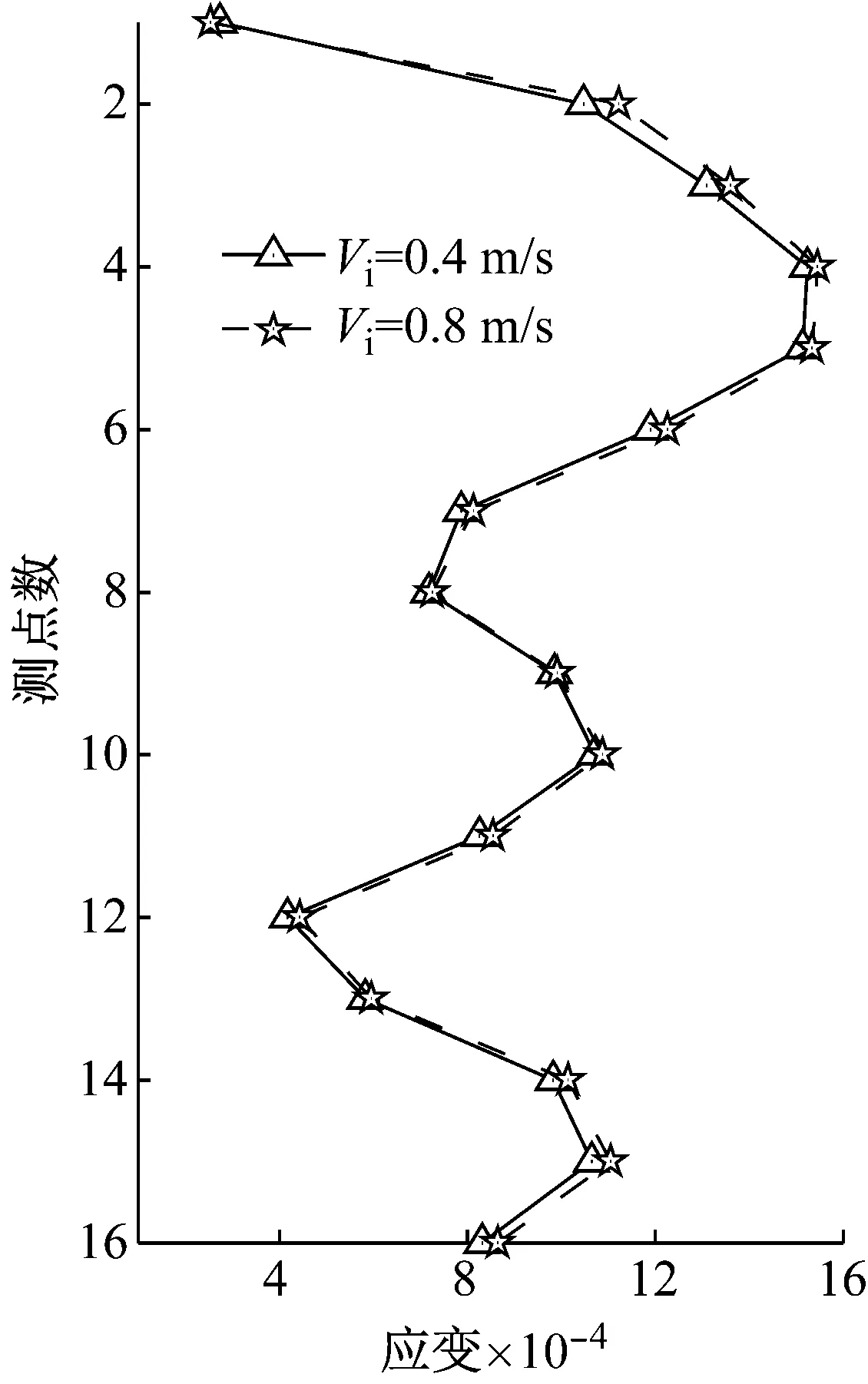
(b) Aim=0.5 m，Tim=3 s图8 IL向应变RMS结果Fig.8 IL strain RMS value

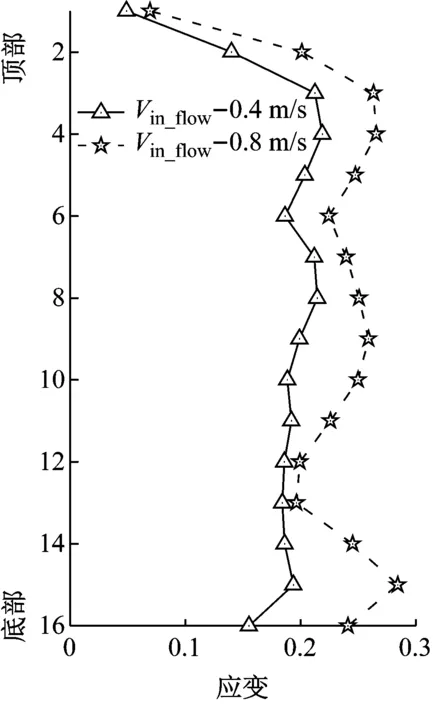
为了细致研究平台运动与内流共同作用下，悬垂立管涡激振动响应特性，将4种工况下16个测点的CF向应变RMS值结果计算出来，如图9所示，分别给出了两种顶端平台运动幅值和周期下，CF方向不同内流速度对应的应变RMS值。

对比图9(a)和(b)，顶端平台运动相同,不同内流速度下应变RMS结果。将平台顶部运动的主导频率设为fim。图9(a)中，平台顶部运动的主导频率设为fim, 内流速度为0.8 m/s时，CF向整体呈现5阶响应模态(2fim)。而内流速度为0.4 m/s时，CF向整体呈现4阶响应模态(fim)。内流速度为0.8 m/s时，CF向整体应变响应RMS值大于内流速度为0.4 m/s时应变响应RMS值。图9(b)中，将平台顶部运动的主导频率设为fim，两种内流速度下CF向应变RMS值变化趋势相近，均为6阶响应模态(2fim)。两种内流速度下，各测点CF向应变RMS值变化各有不同，这说明本试验中的内流流速区间，内流对横流向涡激振动并没有直接确定性的影响规律。

对于在振荡流中横向自由振动的刚性圆柱体，Sumer等[24-27]发现涡激振动的响应频率通常是振荡流频率的整数倍，如式(14)，换言之，在每个运动周期中多个完整的泄涡过程。

(14)

式中：N为每个运动周期中泄涡的对数；fdomi是在振荡流中涡激振动的主导频率(Sumer假设响应频率是不随时间变化的)；fosc是振荡流场的频率，在本文中与顶部的激励频率fim相同。然而，刚性圆柱体的试验结果表明约化速度也会影响N值的大小，这是因为锁定区间对应一定的约化速度区间。通过频率的分布，可以确定，以顶部平台运动Aim=0.7 m,Tim=7 s为例，两种内流速度下的主导频率分别为fim和2fim, 泻涡对数为N≈1和N≈2。这符合Sumer关于泻涡对数一般为整数的结论。

(a) Aim=0.7 m，Tim=7 s

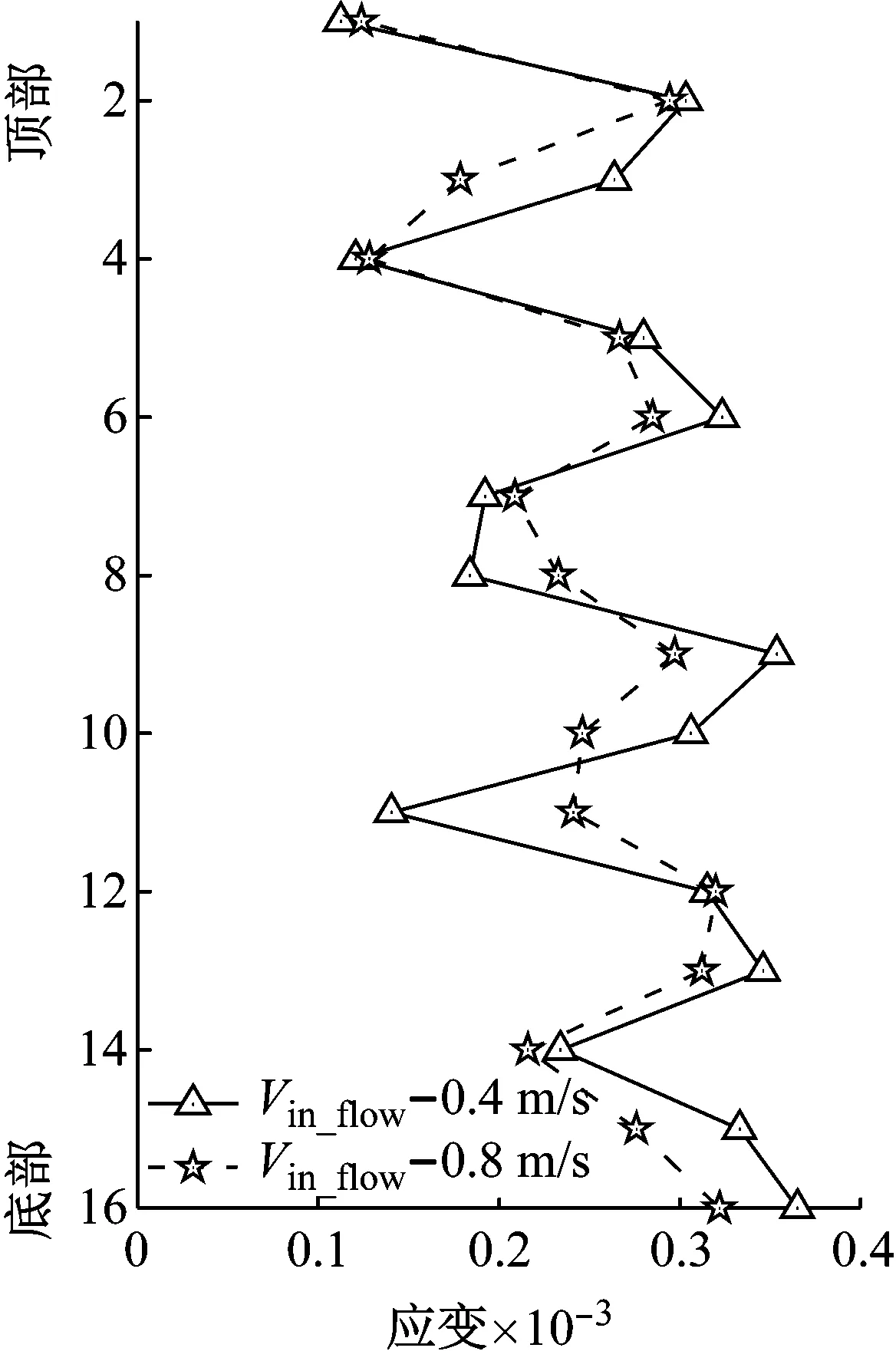
(b) Aim=0.5 m，Tim=3 s图9 CF向应变RMS结果Fig.9 CF strain RMS results

如表4各工况下泻涡对数所示，本文选取工况KC数在19～26。这个区间刚好在N=1，2的转换区间。考虑到KC数还沿立管长度方向变化，这使得平台运动引发的悬垂立管VIV本身就是非常不稳定的。

表4 4种工况综合分析Tab.4 Comprehensive analysis of 4 cases

选取顶端平台运动幅值为0.7 m，周期为7 s的空间响应频率结果具体分析，如图10(a)～10(d)为55.2 s～122.9 s，内流速度为0.4 m/s和0.8 m/s，IL和CF方向，整体应变响应频率结果。图10(a)和图10(c)分别为内流速度为0.4 m/s和0.8 m/s立管IL向响应频率分布图，响应频率和顶端运动频率fim一致。图10(b)内流速度为0.4 m/s时，立管CF向响应频率分布图。可以发现，CF向响应主导频率并不很明晰，接近fim，同时伴有2fim,3fim, 4fim和5fim的谐频，这与悬垂立管局部的KC数分布，泻涡频率分布不同有关。图10(d)内流速度为0.8 m/s时,立管CF向响应频率分布图。可以发现，CF向响应主导频率为二倍的顶部运动频率，接近0.28 Hz，同时伴有fim,3fim, 4fim和5fim的谐频。内流速度为0.8 m/s时，主导频率为2fim，内流速度为0.4 m/s时，主导频率为fim，这说明即使顶部平台运动情况相同，悬垂立管涡激振动响应主导频率依然是不统一的。

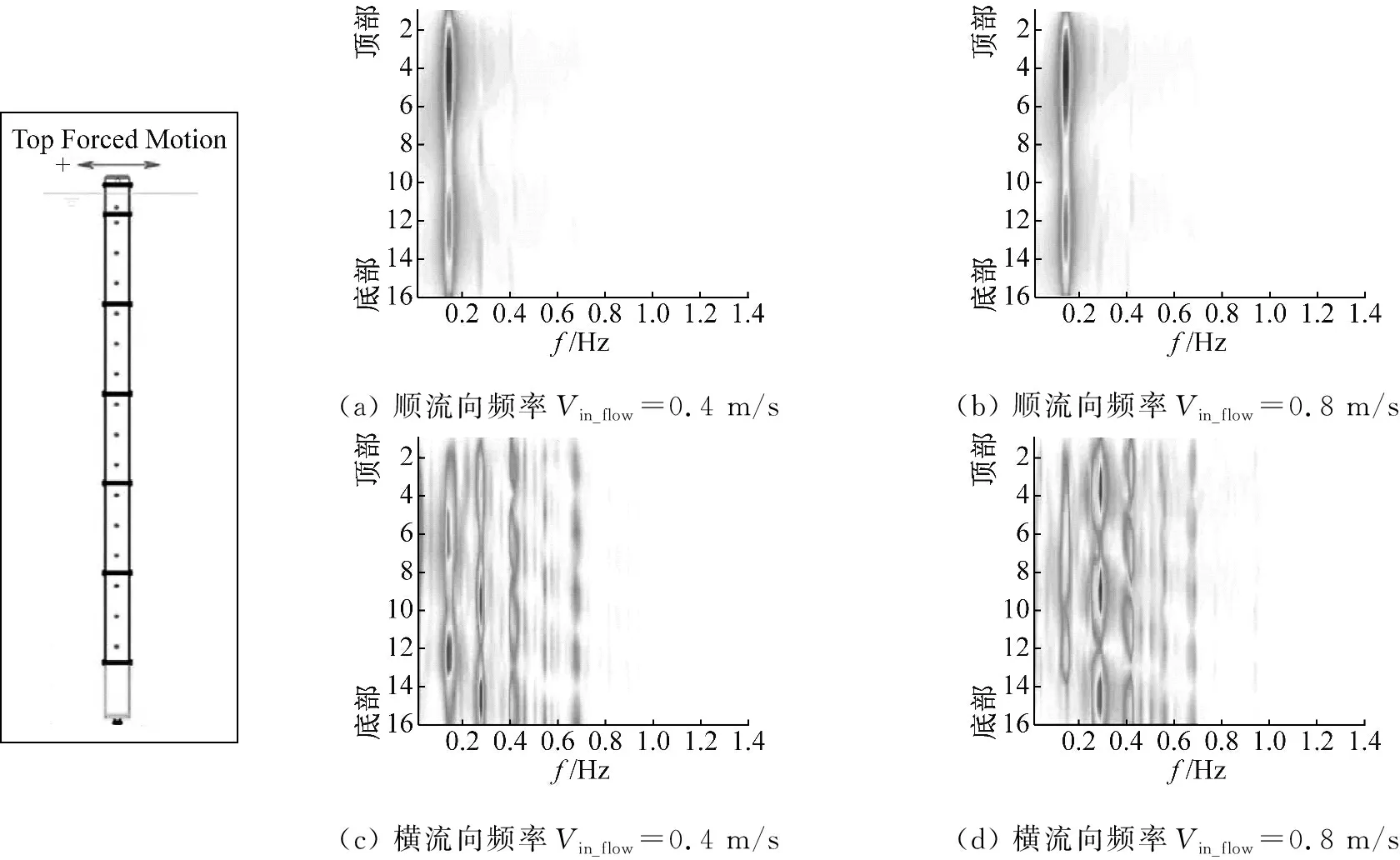
(a) 顺流向频率Vin_flow=0.4 m/s(b) 顺流向频率Vin_flow=0.8 m/s(c) 横流向频率Vin_flow=0.4 m/s(d) 横流向频率Vin_flow=0.8 m/s

图10 整体空间响应频率结果(Aim=0.7 m,Tim=7 s)

Fig.10 The overall space- frequency results(Aim=0.7 m,Tim=7 s)

4 结 论

为了研究自由悬挂抽水管在顶部平台运动和管内流动共同作用下的动力响应特性，本文开展了大尺度悬垂立管水池模型试验。通过不同工况下试验结果的分析，以及和ORCAFLEX数值模拟结果的对比，获得以下主要结论：

(1) 通过IL向全局响应的分析，发现IL向法向速度具有行波特征，立管的顺流向法向速度沿着管长方向有不同异向速度的变化。 各点KC数幅值、泻涡频率幅值呈现类似“波浪状”分布，但整体呈现减小趋势。

(2) 本试验内流流速区间对于顶部张力影响不大；基于数值模拟的结果，发现不同内流流速下KC数以及fst幅值相差不大；同种顶部平台运动情况，不同内流流速下，平台运动诱导的横向涡激振动响应特性与内流速度大小并没有绝对相关性。

(3) 大管径悬垂立管在振荡流场和内流共同作用下，可以产生涡激振动，即使内流对结果影响不大，同种平台运动下，悬垂立管涡激振动响应结果仍有差别,证明了顶部平台运动诱发的涡激振动具有不稳定性。