不等跨变轴径四支承曲轴支反力分析计算

张顺平，雷文刚，李 奎

(重庆水泵厂有限责任公司国家企业技术中心，重庆 400033)

目前，在常用设计手册里[1-4]一般只能查阅到曲轴每跨跨距、轴径及载荷相同情况下超静定梁各支承处的支反力计算系数，不能查阅到不同跨距、轴径及载荷的支反力计算系数，因此给曲轴的受力分析及支承处轴承的寿命计算带来很大难度。为了解决这个问题，本文通过对“曲轴每跨跨距、轴径及载荷相同的超静定梁的支反力计算”模型的扩展，建立了“曲轴每跨跨距、轴径及载荷各不相同的超静定梁的支反力计算”模型，并建立了该模型下的支反力计算公式。

1 模型建立

曲柄连杆机构常被用作将旋转运动转化为往复运动的转换机构，而在曲轴上设计的连杆机构则是常见的一种结构布置形式。曲轴在旋转过程中，每一拐的连杆受力都随转角的变化而变化，因此曲轴两端及中间支承处的支反力也是随曲轴转角变化而变化[5]。为了能精确计算曲轴受力及曲轴支承处轴承受力，就需要根据每拐连杆随转角变化的力来分析计算曲轴各处的支反力。

曲轴的支承一般都是采用滚动轴承或滑动轴承，因此可以将曲轴支承简化为简支横梁的模型。而本文讨论的是四支承曲轴，因此属于横梁简支超静定的计算范畴。

为计算各支承处的支反力，本文中建立的计算模型满足以下条件：1)曲轴上有4个支承，且输入端为悬臂梁结构形式；2)每跨的跨距及轴径都不相同；3)每个载荷大小不同，且每跨最多受2个集中载荷及输入端受1个悬臂集中载荷(如皮带轮或外挂齿轮载荷)。

在曲柄连杆机构[5]的受力分析中，可将曲轴支反力简化为如图1所示的连续梁超静定简支梁模型进行计算。

图1 三跨四支承简支梁

该模型中符号的含义见表1。

表1 符号说明

2 受力分析与计算推导

2.1 标准三弯矩方程式

在材料力学及建筑结构静力学[1-2]中，其标准三弯矩方程如下：

(1)

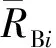
2.2 虚反力计算模型

1)单跨中间1个虚拟集中载荷的虚反力。

在连续简支梁中[2]，单跨1个虚拟集中载荷的虚反力模型如图2所示，其虚反力分别为：

①简支座A的虚反力。

(2)

②简支座B的虚反力。

(3)

图2 单跨1个虚拟集中载荷虚反力

2)单跨中间2个虚拟集中载荷的虚反力。

常规设计资料里[2-4]，对连续简支梁只给出了“单跨对称2个虚拟集中载荷的虚反力计算”，未对“非对称2个虚拟集中载荷的虚反力计算”进行分析，本文结合“单跨中间1个虚拟集中载荷的虚反力计算”，分别按“F1与作用距离a”和“F2与作用距离b”的虚反力进行力的合成，其模型如图3所示，结合式(2)、(3)经过推导得：

①支承弯矩。

MA=MB=0

(4)

②简支座A的虚反力。

(5)

③简支座B的虚反力。

(6)

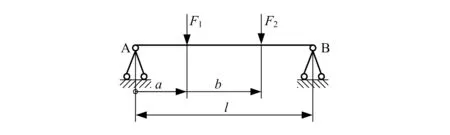
图3 单跨2个虚拟集中载荷虚反力

3)单跨一端1个虚拟弯矩载荷的虚反力。

在连续简支梁中[2]，单跨一端1个虚拟弯矩载荷的虚反力模型如图4所示，其支承弯矩的计算公式与式(4)相同，虚反力的计算公式分别为：

①简支座A的虚反力。

(7)

②简支座B的虚反力。

(8)

图4 单跨一端1个虚拟弯矩载荷虚反力

2.3 建立中间各简支座的三弯矩方程式

图1中，由于连续支梁两端简支座0和3处没荷载[1]，因此弯矩M0=M3=0，结合式(1)可以分别列出简支座1和2处的三弯矩方程式。

简支座1的三弯矩方程式：

(9)

简支座2的三弯矩方程式：

(10)

2.4 各外载荷对各简支座的虚反力计算

1)第1跨的虚反力计算。

该跨有载荷F1和F2，按照式(4)、(5)、(6)对第1跨求其虚反力：

(11)

(12)

2)第2跨的虚反力计算。

该跨有载荷F3和F4，按照式(4)、(5)、(6) 对第2跨求其虚反力：

(13)

(14)

3)第3跨的虚反力计算。

该跨的载荷有F5,F6及F7对简支座3的弯矩MF7=-F7a。因此先分别求出每个载荷对该跨的虚反力，然后将简支座A和B的虚反力合成。

①该跨载荷F5和F6对简支座A、B的虚反力，按照式(4)、(5)、(6) 对第3跨求其虚反力：

(15)

(16)

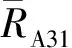
②该跨载荷MF7=-F7a对简支座A、B的虚反力，可按照式(7)、式(8) 对第3跨求其虚反力：

(17)

(18)

根据式(15)～(18)，即可以求出该跨总的虚反力：

(19)

(20)

2.5 各简支座弯矩的计算

将式(11)～(20)代入式(9)和式(10)中求解得到各简支座的弯矩：

2.6 各简支座支反力的计算

根据外载荷F1～F7及式(21)中的各弯矩，可以求解各简支座的支反力。

1)简支座0处支反力计算。

在简支座1处将连续简支梁截断，取左边杆件进行分析。因为R0l1-F1(l1-a1)-F2(l1-b1)=M1,所以有

(22)

式中：Ri为支座i处的支反力，i=0,1,2,3。

2)简支座1处支反力计算。

在简支座2处将连续简支梁截断，取左边杆件分析得：

R0(l1+l2)+R1l2-F1(l1+l2-a1)-F2(l1+l2-b1)-F3(l2-a2)-F4(l2-b2)=M2

所以有

(23)

3)简支座2处支反力计算。

在简支座3处将连续简支梁截断，取右边杆件分析。因M3=-F7a，分析得：

R0(l1+l2+l3)+R1(l2+l3)+R2l3-F1(l1+l2+l3-a1)-F2(l1+l2+l3-b1)-F3(l2+l3-a2)-F4(l2+l3-b2)-F5(l3-a3)-F6(l3-b3)=M3

所以有

R2=

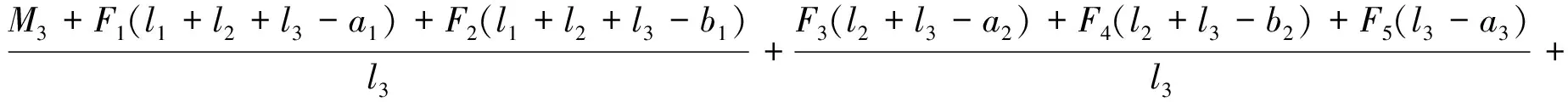
(24)

4)简支座3处支反力计算。

在简支座2处将连续简支梁截断，取右边杆件进行分析。因R3l3-F3a3-F6b3-F7(l3+a)=M2，所以有

(25)

3 公式验证

3.1 验证方法

1)按《机械设计手册》中特例进行验证。

令F1=F3=F5=F，F2=F4=F6=F7=0，b1=b2=b3=a=0，I1=I2=I3=I，l1=l2=l3=l，a1=a2=a3=l/2。将按本文公式计算得到的结果与按《机械设计手册》[4]计算得到的值进行比对，结果见表2。

表2 与《机械设计手册》算得支反力的比对结果

2)用MADYN2000转子动力学专用软件进行验证。

令F1=1 000N，F2=1 500N，F3=2 000N，F4=2 500N，F5=3 000N，F6=3 500N，F7=1 200N，l1=l2=l3=150mm，a=200mm，a1=a2=a3=50mm，b1=b2=b3=105mm，第1跨外径do1=90mm、内径di1=45mm，第2跨外径do2=105mm、内径di2=45mm，第3跨外径do3=120mm、内径di3=45mm，悬臂端外径do4=90mm、内径di4=45mm。分别用MADYN2000转子动力学专用软件与本文计算公式进行计算比对，其比对情况如下：

①通过转子动力学专用软件MADYN2000建立模型，模型及计算结果如图5所示。

图5 MADYN2000软件建模及计算结果

②比对两种计算方法获得的支反力结果。

本文公式与MADYN2000转子动力学专用软件计算得到的支反力比对结果见表3。

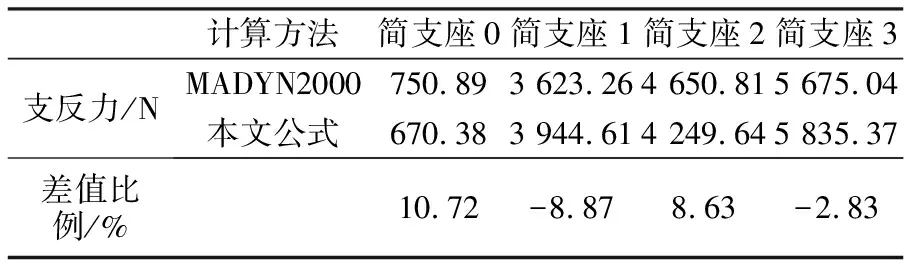
表3 与MADYN2000转子动力学

3.2 验证结果分析

《机械设计手册》中是直接给出支反力系数，没有给出计算公式，因此采用特例验证方式验证了本文公式的正确性。

由于MADYN2000转子动力学专用软件采用的是有限元计算分析法，在计算时边界条件有细微差异，导致结果也有一定偏差，但二者的计算结果是高度吻合的。

本文计算公式是用三弯矩方程求解简支梁理论推导出来的，该公式的计算结果与《机械设计手册》结果完全吻合，且与MADYN2000转子动力学专用软件计算结果高度吻合，由此可知，本文计算公式是完全正确的。

4 结束语

本文介绍的不等跨变轴径四支承曲轴支反力分析计算方法，为四支承曲轴支反力计算提供了快速、精确的计算依据，也为以后曲轴及轴承受力分析提供了可靠的数据，具有较高的工程实际意义。由于本文只是从理论上进行研究，与实际应用可能还存在一些差异，以后可结合工程实际应用进行验证以获得修整系数，使其达到与工程实际应用的高度吻合。