基于瞬态温升仿真的列车制动盘结构研究
左建勇,刘家良,胡 果,顾亦豪
(同济大学铁道与城市轨道交通研究院,上海 201804)
制动技术是影响列车提速的重要因素,制动盘作为列车制动系统的核心部件,直接影响列车的安全性能。在高负荷制动情况下,制动盘与闸片之间的摩擦使制动盘快速升温。研究表明,制动盘升温的过程可能导致摩擦副磨损增加、制动效率下降和制动盘热疲劳开裂[1]。此外,摩擦盘上的温度不均匀分布会导致制动盘变形不均匀,从而使得摩擦副的局部过载。因此研究高速列车制动过程中制动盘的温升规律,对保证列车行车安全具有实际的工程意义。
目前,国内外研究人员对制动盘进行了大量研究,主要集中在制动盘/闸片材料及其匹配研究、制动盘热-力耦合研究、制动盘性能研究(温度场、应力场等)以及制动盘疲劳磨损研究[2-3]。对于制动盘温度场,研究主要集中在制动盘材料和运行参数变化对温度场的影响。然而随着列车速度的提高,制动过程中车辆的动能给制动盘带来了巨大的热负荷,对制动盘来说是全新的考验,因此优化制动盘结构设计、改善制动盘温度场分布情况,具有非常重要的意义。
1 制动盘有限元模型建立
以300km/h高速列车实施盘形制动的真实工况为例,仿真模拟列车由制动开始到停车的过程中制动盘温度场的分布情况。制动盘为柱状散热筋结构,两侧的摩擦面通过中间的柱状散热筋相连,每轴制动盘数为2。紧急制动时,列车速度从300km/h降到200km/h时对应的平均减速度为0.8m/s2;速度从200km/h降到0时对应的平均减速度为0.92m/s2[4]。列车速度v(t)的表达式如下:
(1)
式中:t为时间,s。
1.1 仿真模型
在SolidWorks中建立制动盘三维模型,如图1(a)所示。该制动盘为圆柱状散热筋结构,结构主要参数:外径为640mm,摩擦面宽度为145mm,整个制动盘厚度为80mm,其中盘体厚度为20mm,散热筋长度为40mm、直径为20mm。将三维模型导入到ANSYS中,运用8节点Solid70单元对模型进行网格划分。由于制动盘在结构和载荷上都具有循环对称性,为方便仿真计算,取制动盘圆周方向1/4结构进行瞬态温升仿真,如图1(b)所示。由于在盘面上要同时施加热流密度与对流散热系数,为了避免两者冲突造成施加失效,在制动盘摩擦表面上建立了表面效应单元Surf152,在Surf152上施加对流散热系数,在摩擦面对应网格上施加热流密度。
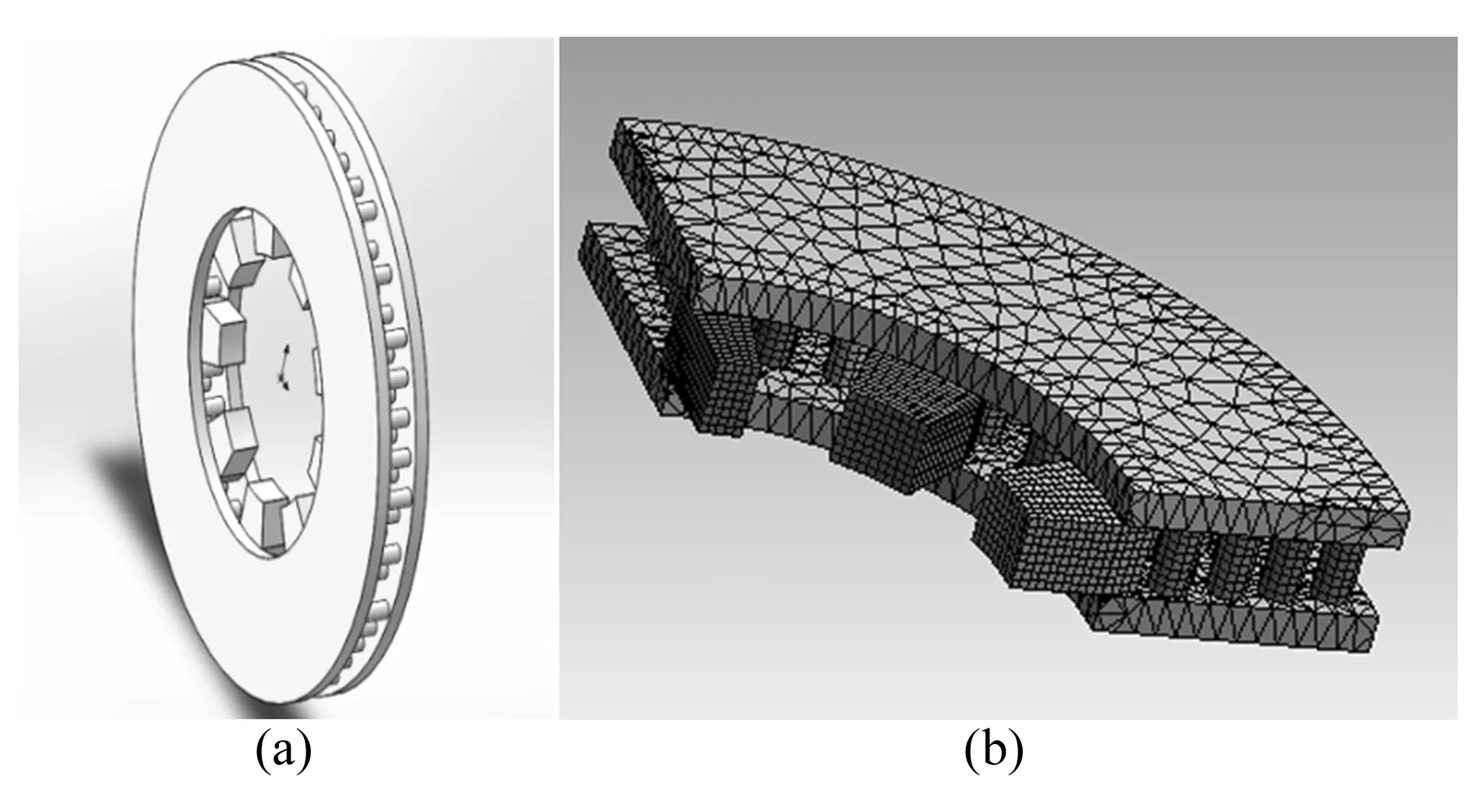
图1 制动盘几何结构及有限元模型
改变制动盘结构,从散热筋形状、直径、疏密以及制动盘盘体厚度4个角度,建立不同结构的制动盘模型,对应结构参数见表1。散热筋形状分为圆形、菱形、长方形,但散热总面积相等,如图2(a)左侧所示。散热筋直径取10,15,20,25mm,如图2(a)右侧所示。散热筋疏密情况如图2(b)所示,径向上均匀分布4个散热箱,周向上分布5,7,9,11个散热筋,为了更清楚地表示,在表1中用周向上相邻散热筋的夹角度数来表示散热筋的疏密情况。另外图中4-5*所示为在图中4-5所示结构的基础上增加了摩擦位置对应的散热筋数量。盘体厚度为16,20,24,28,32mm,如图3所示。
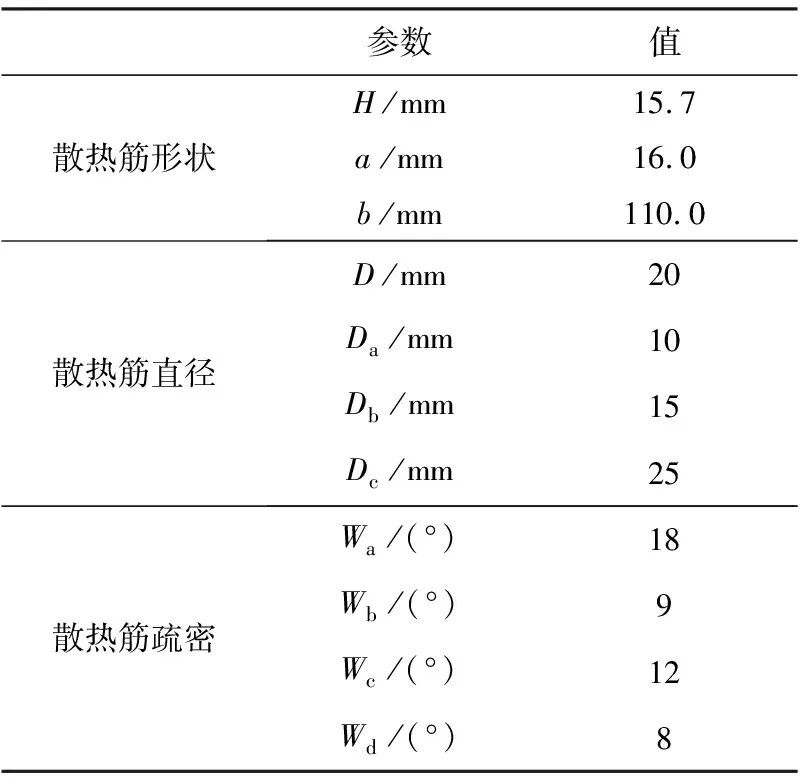
表1 制动盘结构参数
1.2 热流密度

图2 不同参数结构制动盘几何模型
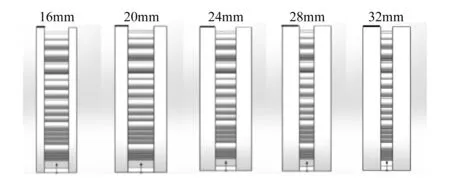
图3 不同盘体厚度制动盘模型
制动过程中,制动盘与闸片相互接触摩擦,列车的动能转化为热能,热载荷以热流密度的形式施加在制动盘面上。热流密度等于单位面积上摩擦力在单位时间内所做的功。在制动盘温度场的分析中,热流密度普遍采用能量折算法。该法认为热量在摩擦面上均匀分布,然而在实际制动过程中,制动盘与闸片接触区域是绕制动盘中心做圆周运动的,摩擦面上热量分布是不均匀的[5]。在制动盘温度场仿真过程中,为了实现热源移动,用函数形式输入周向循环移动热源[6-7]。热流密度计算公式如下:
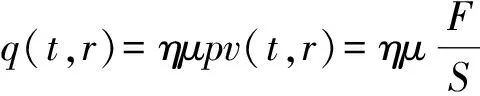
(2)
式中:q(t,r)为时刻t制动盘表面上半径为r处吸收的热流密度,J/(m2·s);η为热流分配系数,即制动盘所分配到的摩擦热所占比例;μ为摩擦因数;p为比压,N/m2;v(t,r)为时刻t制动盘表面上半径为r处的速度,m/s;F为制动盘侧的闸边压力,N;S为闸片的有效接触面积,m2;ϖ为制动盘的角速度,rad/s。热流分配系数的表达式为:
(3)
式中:kd,cd,ρd,Sd和kp,cp,ρp,Sp分别为制动盘和摩擦片的热传导系数、比热、密度和摩擦面积。
运用APDL编程,用函数的形式输入周向循环移动热源,施加移动热源流程如图4所示。
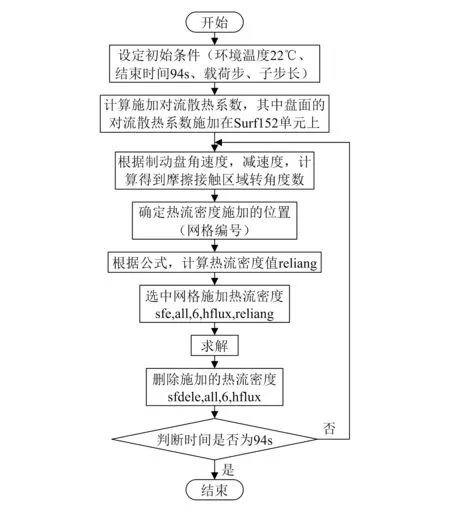
图4 移动热源流程图
1.3 对流散热系数
对于制动盘的不同部位考虑使用不同的热对流模型[8]。
1)制动盘面,对流传热形式为纵掠平板对流传热。
(4)
式中:hc为对流散热系数,W/(m2·K);Pr为普朗特数,本文取0.703;Re为雷诺数;λa为空气的导热系数,本文取2.59×10-2W/(m·K);L为特征长度,m。
雷诺数计算公式[9]如下:
(5)
式中:v为列车速度,m/s;ρa为空气密度,本文取1.13kg/m3;μa为空气动力黏度,本文取1.91×10-5Pa·s。
2)制动盘圆周面,对流传热形式为横掠单管对流传热。
(6)
式中:C,n为由实验确定的常数,可根据雷诺数查传热学表,见表2。

表2 不同雷诺数对应的C,n参数表
3)散热筋,依据传热学定律属于横掠管束对流传热形式。
(7)
2 制动盘瞬态温度场分析
对高速列车制动盘进行瞬态热分析,得到制动盘的温度场分布云图,如图5所示。制动盘最高温度出现在第66.3s,最高温度为643.95℃,如图5(a)所示。

图5 制动盘温度场云图
制动过程中制动盘的最高温度并不是出现在制动结束时刻。在制动初期,进入制动盘摩擦面的热量大于制动盘表面由于对流、辐射以及向内部进行热传导而流失的热量;而在制动后期,由于闸片制动盘相对速度降低,输入盘面的热量减少,同时盘表面向盘体持续进行热传导,制动盘表面温度开始下降,盘内温度继续升高,制动盘最高温度下降。
图6给出的是制动盘表面同一径线(角度为0°)不同半径位置的温度时间历程。从图6中可以看出,在整个制动过程中,制动盘靠近内径处的温度相对较低。摩擦区域(半径位于183mm至305mm)温度较高且沿径向变化较小。在摩擦接触区域,周向接触长度较长的区域温度上升速度相对较快,如r为280mm的位置,而位于周向接触长度较短的区域,在制动开始时表面温度上升比较缓慢,如r为210mm的位置。对于摩擦接触区域外的位置,如r为175mm及310mm,可以看到温度上升速度较慢且最高温度较低,这是由于该处不参与盘片直接接触摩擦,这些部位的热量是从摩擦区域向该区域传递的,热量传递需要一定时间。
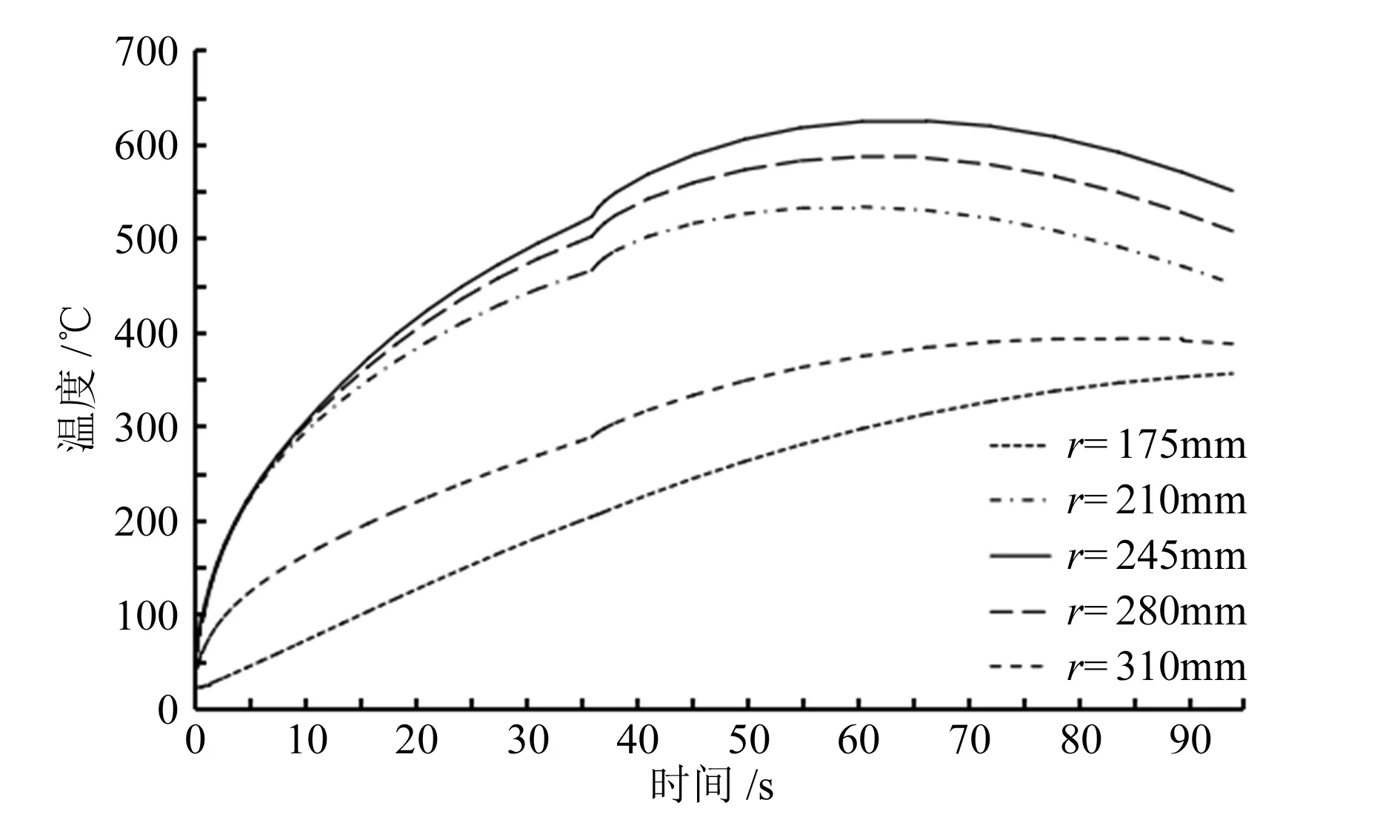
图6 盘面径向位置节点温度时间历程
图7给出的是制动盘距摩擦面不同厚度位置(角度为0°,半径为282mm)节点温度时间历程。可以看到盘体靠近摩擦面的区域温度上升较快,距摩擦面较远的盘体内部区域则温升速度相对较缓,随着时间的推移,沿厚度温度差值开始变小。这是由于制动过程中,摩擦面温升是由盘片摩擦生热导致的,而制动盘盘体内部的温升主要是靠制动盘摩擦面的传导,热传导需要一定的时间,因而盘体内部温度呈现缓慢上升的趋势。随着制动过程的进行,制动盘与闸片的相对速度减小,靠近摩擦面处节点温度开始下降,沿厚度方向节点温度持续升高,导致制动盘沿厚度方向的温度差值逐渐变小。
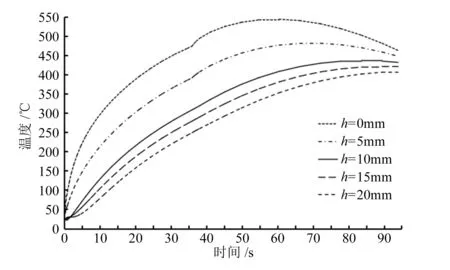
图7 盘体厚度位置节点温度时间历程
3 结构参数影响规律分析
针对不同的散热筋形状、直径、疏密以及盘体厚度,对制动盘温度场进行数值模拟,其中工况、材料等设置均相同。不同结构参数制动盘对应最高温度如图8所示。
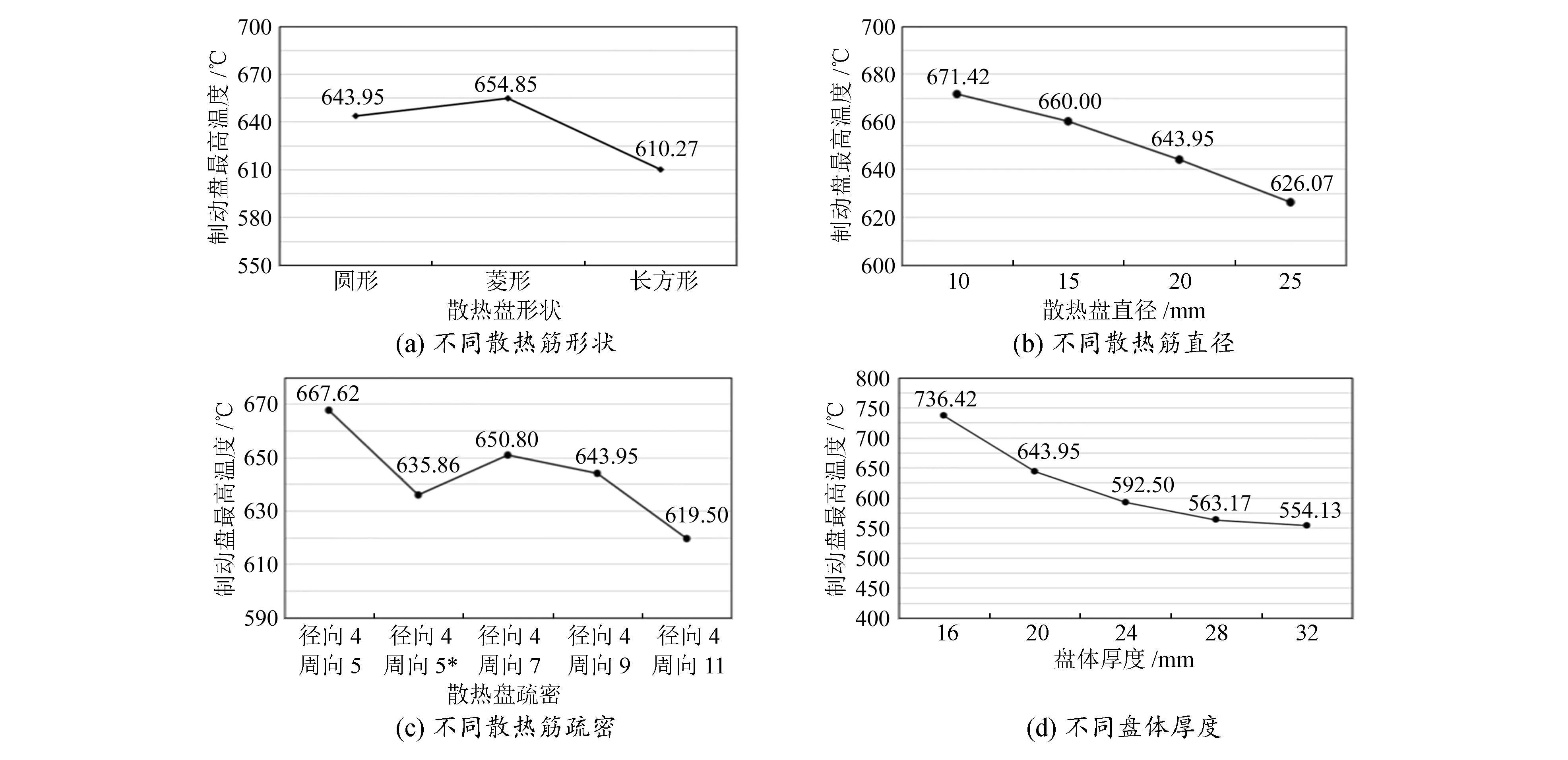
图8 不同结构参数制动盘最高温度
从图8(a)可以看出,就散热筋形状而言,散热筋面积相同时,采用圆形相比采用菱形制动过程中的最高温度较低;采用长方形相比采用圆形能降低制动盘最高温度5.3%。
从图8(b)可以看出,增大散热筋直径可以降低制动盘最高温度。由式(7)可知,增大散热筋直径即增大散热筋特征长度,会导致散热筋处的对流散热系数减小。但随着散热筋直径增大,对流换热面积也随之增大,有利于制动过程中制动盘和空气的对流换热,从而降低制动盘最高温度。
从图8(c)可以看出,增加散热筋数量可以降低制动盘最高温度。对比图8(c)中的径向4周向5与径向4周向5*两种情况对应的制动盘最高温度,可知增加摩擦区域对应的散热筋的数量,可以降低制动盘最高温度4.76%。这是由于温度在制动盘径向上并不是均匀分布的,而是集中在摩擦面对应的区域。制动盘闸片摩擦产生的热量由制动盘表面摩擦接触区域向盘体内部进行热传导,增加摩擦区域对应的散热筋的数量,可以加强制动盘高温区域的散热,从而降低制动盘最高温度。
图8(d)反映了制动盘最高温度与制动盘盘厚的关系,从图中可以看出,制动盘盘厚由16mm增加至32mm时,制动盘最高温度降低,但温度降低速度随盘厚增大而减缓。
4 制动盘最高温度函数模型
近似模型技术是一种省时省力的建模优化方法。采用近似模型法对具有圆柱状散热筋且散热筋间夹角为10°的制动盘进行分析,得到制动盘最高温度函数模型。在结构设计中引入近似模型,可以明显加快优化的搜寻速度。本文选用简化的二次多项式形式表示响应面函数[10],省去交叉项,表达式如下:
(8)
式中:y为样本点的响应值;xi为基本变量;α,βi,γi为待定系数,i=1,2,…,N,其中N为涉及点的个数。
确定响应面函数的系数之后,需要对方程的拟合程度以及显著程度进行检验。检验方程拟合程度,需要在对数据进行回归分析后采用调整决定系数来反映响应面的拟合情况,决定系数越接近1,则说明近似模型的拟合性能越好。
(9)
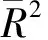
用统计量F检验方程显著程度,表达式如下:
(10)
一般情况下可以通过考量对应的置信水平(Sig.)来判断自变量与因变量之间的关系。置信水平是对方程的总体检验标准,用来考察整个方程有没有使用价值。若置信水平小于0.05则说明方程是显著的,即自变量与因变量之间存在显著的函数关系。
本文采用SPSS软件对仿真结果数据进行处理[11]。针对具有圆柱状散热筋且散热筋间夹角为10°的制动盘,在制动工况等条件不变的情况下,取制动盘最高温度为因变量,盘体厚度h(mm)及散热筋直径d(mm)为自变量,进行回归分析,得到制动盘最高温度T的函数模型:
T=1 366.912-52.127h+0.855h2+1.725d-0.132d2
(11)
对响应面模型进行检验,表3、表4给出了用SPSS进行线性回归的实验结果。从表3可以看到决定系数R为0.999,调整决定系数R2为0.998,均接近1,说明模型拟合良好。表4给出了回归方程的方差分解及检验结果,回归方程的置信水平为0.003,远比常用的置信水平0.05要小,因此方程是显著的。

表3 回归方程拟合总结

表4 回归方程方差分解
5 结束语
本文结合列车运行参数,从散热筋形状、直径、疏密以及盘体厚度出发,运用移动热源法,实现了制动盘温度场的数值模拟,并对比分析了制动盘结构变化对制动盘温度场的影响规律。通过建立制动盘最高温度面响应模型,得到的制动盘最高温度与散热筋直径以及盘体厚度之间的函数关系,对制动盘的结构优化设计具有一定参考意义。由于试验环境、试验方法等条件限制,文中涉及的数值模拟结果并没有试验数据做支撑,文章中得到的规律均是基于仿真结果得到的,今后的研究重点将是实车试验。

