简支梁模态参数方法的研究

王国梁 王继争

(安徽富煌钢构股份有限公司，安徽 合肥 230088)

0 引言

随着现代文明的进步和土木工程日新月异的更替，桥梁在人们生活中所起的作用越来越大。在桥梁结构的健康监测、损伤识别中，模态参数(固有频率、阻尼和振型)具有重要意义[1]。本文将借助QY型倾角仪对简支梁结构进行模态参数识别，运用理论和实验的方法得出简支梁的模态参数(固有频率、阻尼比、固有振型)。从而得出简支梁在环境激励下，用倾角仪测试其模态参数的可行性，为复杂结构的振动测试做参考。

1 简支梁结构参数

实验中所研究的是等截面简支梁，结构简图如图1所示。并对该结构做以下假定：不计简支梁的轴向变形；简支梁在振动时，其横截面与简支梁的轴向始终保持垂直。简支梁的结构参数为：长L=2.7 m，宽B=0.2 m，高H=0.01 m，密度ρ=7.8×103kg/m3，材料弹性模量E=2.2×1011N/m2。实验时，在自然环境激励下做该实验，为了减少人为因素的影响，实验人员应保持安静，周围无大型机械运转。

2 简支梁的理论分析

设q(x,t)是简支梁上的均布力，由牛顿第二定律可得简支梁在弯曲振动时的偏微分方程及以下两式：

(1)

(2)

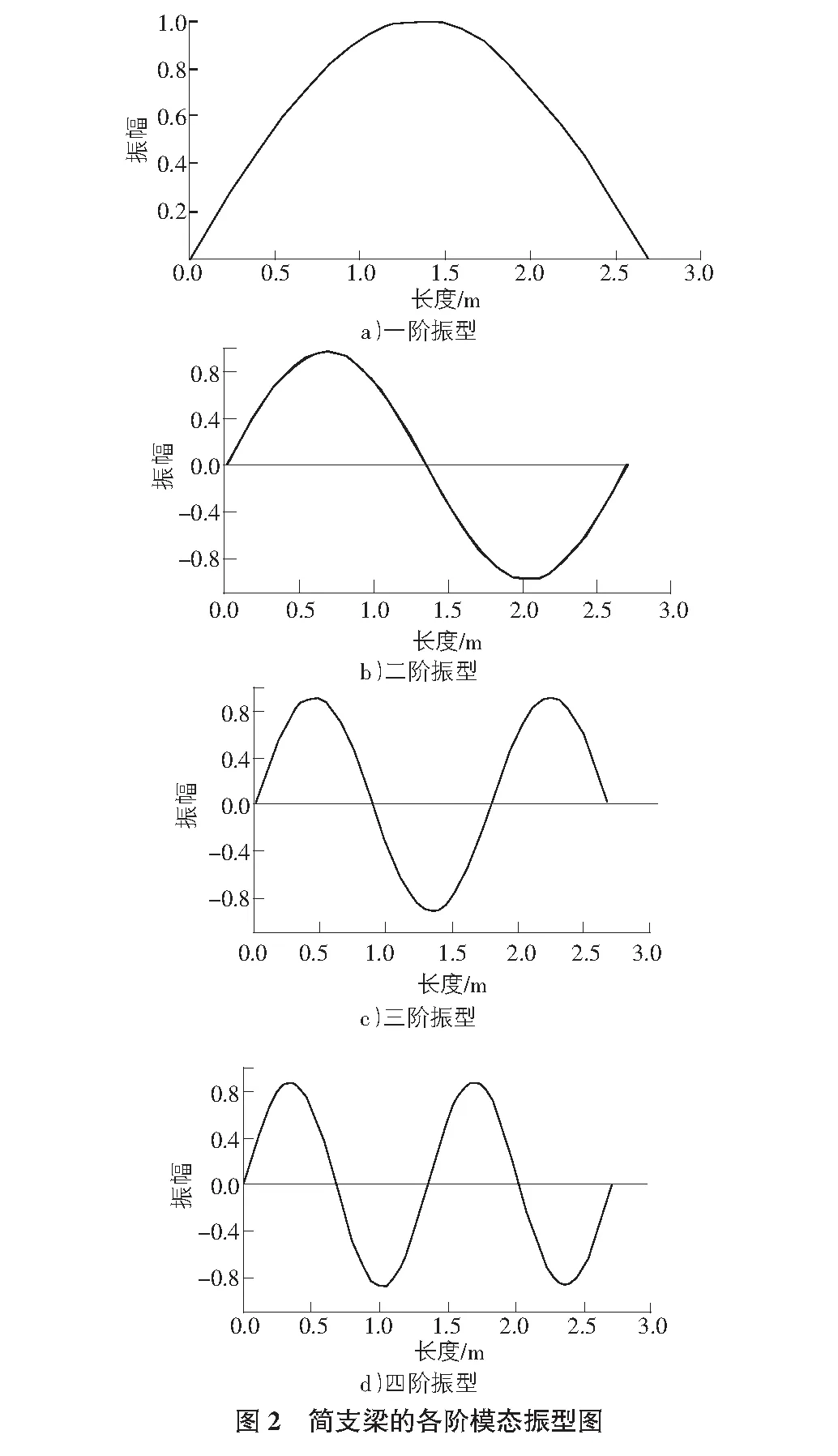
将简支梁的参数代入到式(1)，式(2)可得简支梁的固有频率和振型。前四阶的固有频率为：9.4 Hz，36.4 Hz，88 Hz，142.3 Hz。由式(2)通过fortran编程可得各阶振型的数据[2]，各阶固有振型如图2所示。

3 简支梁模态识别实验

3.1 实验原理

理论上，简支梁仍然是无限自由度体系，即具有无限个固有频率和固有振型。由结构动力学可知，梁的振动是无穷多个主振型的叠加。但是在环境激励下，含有简支梁的某阶固有频率时，此时简支梁的振动将由该频率产生的振动作为主导，其他由各阶振型产生的影响可忽略不计。

3.2 简支梁固有频率识别

实验仪器布置如图3 所示。试验中，由于交流电压信号的干扰，在互谱中会出现50 Hz倍数的干扰频率。识别的前四阶固有频率值如图4所示。

由图4读出该简支梁的前四阶固有频率：9.2 Hz，34.2 Hz，85 Hz，138.6 Hz。由表1可看出：由倾角数据得到的固有频率和理论值大致相同。

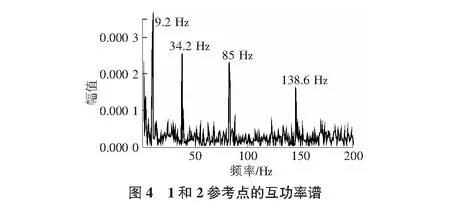
表1 固有率识别的结果比较

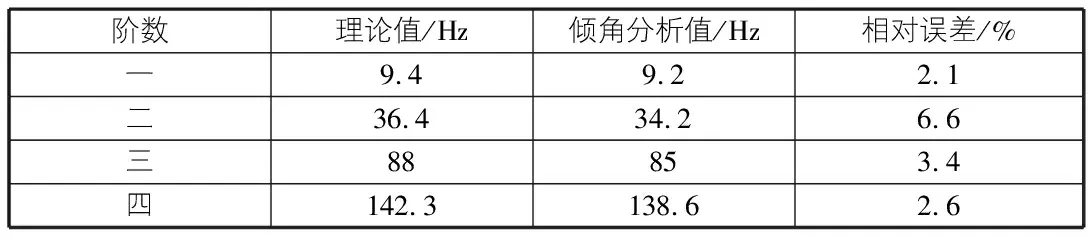
阶数理论值/Hz倾角分析值/Hz相对误差/%一9.49.22.1二36.434.26.6三88853.4四142.3138.62.6

3.3 简支梁振型识别

倾角仪收集数据时：简支梁两端的测点收集到的倾角值大，而对应的结构中的振型位移较小；简支梁中间部位的倾角值小，而对应的振型位移较大。所以对倾角仪收集到的数据经互功率谱变换后也会得到相应的结果。以一阶振型的数据为例说明，采用求倒数法对互功率谱后的数值结果进行处理，如表2所示。由表2中的各测点的数据并经过最小二乘拟合法拟合后，可得结构的一阶模态振型，其他各阶模态振型也可得到，如图5所示。

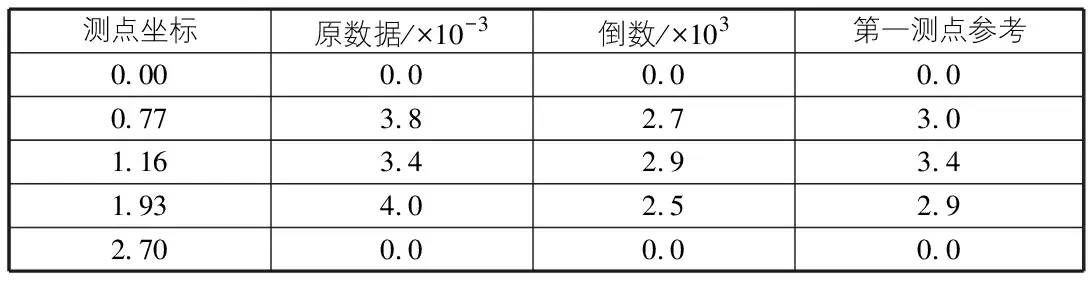
表2 一阶振型的数据

该方法识别的简支梁的各阶模态振型同理论数据得到的结果具有一致性，验证了用倾角仪进行结构模态测试的科学性。

4 结语

本文通过对简支梁模态实验的研究，发现利用倾角仪数据得到的固有频率值同理论值大致相同，并且符合比例关系。同时简支梁的固有振型也符合理论要求。因此用倾角仪进行桥梁模态识别具有可行性[3,4]。