量子纠缠与宇宙学弗里德曼方程∗
王灿灿
(上海大学物理系,上海 200444)(2018年4月25日收到;2018年5月28日收到修改稿)
1 引 言
在过去的几十年里,量子理论取得了突飞猛进的发展,特别是量子纠缠,因为时空几何可以被看作是代表微观量子态的纠缠结构[1,2].如果两个粒子的波函数不能写成它们各个部分的直积,那么它们之间就存在纠缠.如果一个体系存在量子纠缠,那么通过观察体系中的一部分信息可以了解另一部分的信息.量子纠缠的提出是为了解决许多非局域性物理问题,是量子体系中一种非局域性关联,通过研究量子纠缠可以了解微观事物间的新的关联方式.量子纠缠是可观测的,其中,纠缠熵是量子信息的测度.纠缠熵是一个比较基础的物理量:在凝聚态理论中,它用来区分新的拓扑相或不同的临界点;在量子场理论的背景下,纠缠熵可以作为规范理论中相变的一个有用的探针;此外,它在讨论重整化群流的结构中也有新的应用.纠缠熵一直被认为是黑洞熵的起源,而对于纠缠的考虑也引发了一个关于霍金辐射和黑洞蒸发性质的新的讨论.纠缠熵在理解时空量子结构中也起着重要作用,以及在反德西特/共形场论(anti-de sitter/conformal field theory,AdS/CFT)对偶理论的讨论中也会有纠缠熵的出现.AdS/CFT对偶理论是以弦论为基础发展起来的,是研究强耦合量子场论比较有潜力的工具,它将规范理论中的强耦合区域与经典引力理论的弱耦合区域联系了起来.
Ryu和Takayanagi[3−5]提出了一个计算时空几何直接的工具——纠缠熵.在边界场理论中选择一个特定的空间区域V研究了V与其补集¯V之间的纠缠熵,在共形场论纠缠与双时空几何(AdS空间)之间构建了一个定量的联系[6].最近,Jacobson[7]通过最大真空纠缠假说得出了半经典爱因斯坦方程,该假说认为小测地球的纠缠熵在给定体积下是最大的,在几何和量子场的一个局部最大对称真空态中给出了一个定性的论据表明爱因斯坦方程暗示了这个假设的有效性.因此,从最大真空纠缠熵假设出发得到了完整的非线性爱因斯坦方程.在几何上,测地球半径的选择远小于任何宏观长度尺度,所以黎曼正则坐标的使用是合理的.Jacobson利用闵可夫斯基时空中变分δgab在黎曼坐标系下计算面积缺陷δA,可得面积缺陷与紫外区的纠缠熵变化δSUV成正比,即δSUV=δA/(4G).总熵变δStotal受到从物质场状态的变化δ|ψ〉所产生的红外区δSIR的贡献,假设小测地球中的真空纠缠熵是极值,总熵变δStotal=δSUV+δSIR就为零,通过进一步利用量子纠缠第一定律δSA=δ〈HA〉,最后可以推导出爱因斯坦方程[7].
本文主要从纠缠的观点理解宇宙动力学,在纠缠是时空的基本元素的假设下展示了如何从纠缠第一定律得出弗里德曼方程.文中采用费米正则坐标(Fermi normal coordinates,FNC)对面积缺陷进行了扩展讨论[8].FNC描述了一个类时测地线并且沿着测地线克里斯托弗符号对有限的空间区域和所有的时间区域是有效的.在宇宙学背景下,FNC只适用于尺度远小于哈勃视界的情况下,弗里德曼方程首先建立在FNC系统中.然后引入共形费米坐标(conformal Fermi coordinates,CFC)[9],在CFC中主要研究的是空间曲率为零的平坦宇宙,弗里德曼方程将会在CFC中再次被推导出来.
下面对量子纠缠第一定律做一个简短的回顾.对于一般量子系统中的任意状态,子系统A的密度矩阵可以描述为这里ρtotal是整个系统的密度矩阵,是A的补集,通过纠缠熵SA描述子系统A与系统其余部分的纠缠.定义冯·诺依曼纠缠熵为
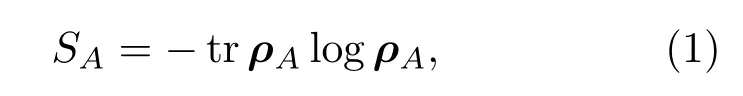
其中ρA为子系统A的密度矩阵,通过哈密顿量定义密度矩阵ρA,
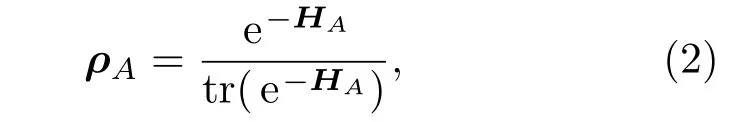
其中,HA是厄米算符,ρA是厄米的且为正,(2)式右边的分母保证了ρA有单位迹.子系统A的纠缠熵的一阶变分为
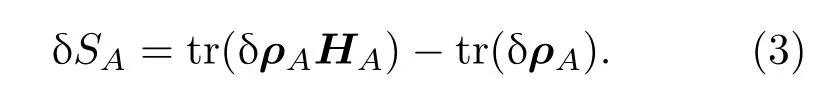
密度矩阵ρA对任何状态都有单位迹,因此最后一项为零,于是得出量子纠缠第一定律
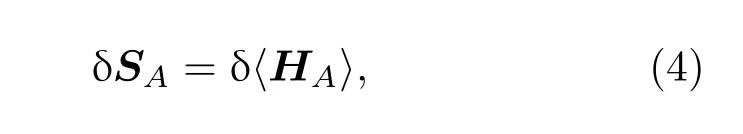
其中哈密顿量HA是根据最初的无扰的密度矩阵定义的.方程(4)被解释为量子纠缠的第一定律,因为它反映了热力学第一定律的一般形式[10].从热状态ρA=eβH/tr(e−βH)开始,方程(4)就可以简化为通常的热力学第一定律δ〈H〉=TδSA.
本文从量子纠缠第一定律出发,结合理想流体的连续性方程,得出宇宙学弗里德曼方程.本文的结构安排如下:第2节简要回顾了FNC的概念;第3节用FNC计算了面积缺陷;第4节和第5节分别讨论了因果结构、纠缠熵变化和弗里德曼方程;第6节通过引入CFC推导出了弗里德曼方程;第7节进行了讨论和总结.
2 费米正则坐标的简要回顾
广义相对论等效原理认为,在一个引力场下惯性参考系中的物理定律在一个无穷小的实验室是有效的.根据等效原理,引力场效应与在平直时空中的加速效应是局部不可分辨的,其实热力学中的物理概念是与观测者有关的.对于一个平直时空的零温情况下,一个自由下落观察者不会感觉到温度,而加速的局域Rindler观测者能同时感觉到温度和观测到熵.在宇宙学中,时间变量与空间变量不同,其中一个特殊的时间变量是测地线观测者的固有时间,而空间随着时间会出现膨胀.在时空中的每一个事件中,时空都是局部平坦的,需要引入黎曼正则坐标,其基本的思想就是用测地线通过一个给定的点定义附近点的坐标.
这里引入FNC[8],然后从几何角度进行构建.我们考虑一个自由下落观测者沿着一个世界线移动,时空坐标为正交平行传播四元组为自由下落观测者的轨迹是一个类时测地线,是观测者O的类时单位切向量形成观测者的局部空间系.通过类空测地线在任意事件Q(τ)正交于世界线可以构造一个局部超曲面.考虑在Q(τ)邻近的一点P,坐标xµ位于这个超曲面上,从Q(τ)到P将有一个独特的时空测地线连接,因此,分别定义Q点和P点的FNC 为满足关系
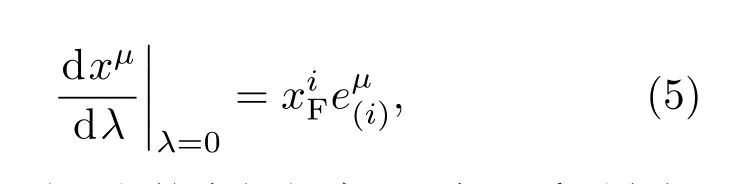
其中λ是从Q到P段的本征长度,因为一系列空间基集是正交的,FNC度规是在O中是成直角的,于是得出
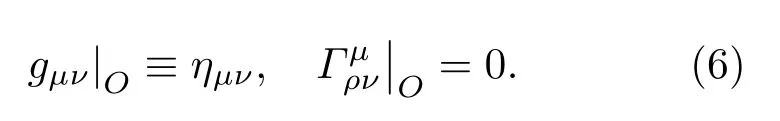
基于以上的研究可以利用xiF逐阶计算FNC,重复使用测地线方程来计算,包括一些坐标系(例如史瓦西坐标)xµ和FNC,然后得到任意坐标xµ和FNC之间的关系:
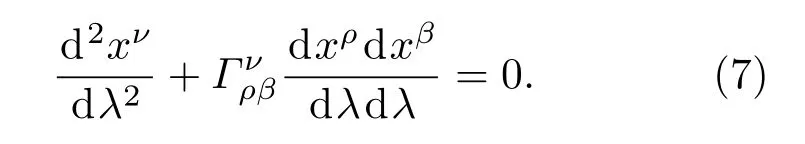
把xµ展开成
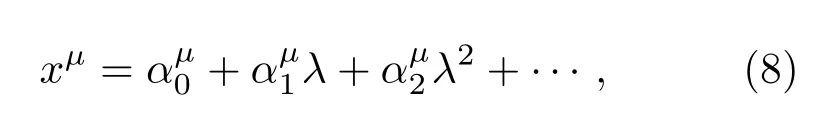
其中
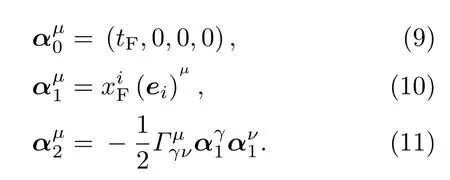
更简单地说,可以把时空元素展开为gµv=ηµv+所以,在FNC下度规为
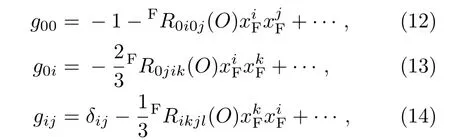
其中FRikjl表示黎曼张量的投影,可以从给定的黎曼张量得出修正.
下面讨论FNC中的弗里德曼-勒梅特-罗伯逊-沃尔克(FLRW)度规.
在笛卡尔坐标系中标准的FLRW度规为
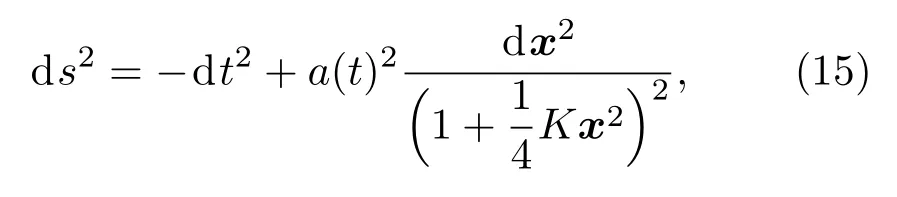

通过下面的度规张量变换得出FNC,
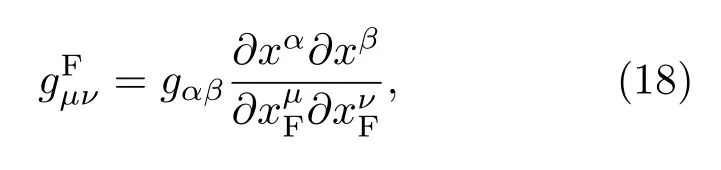
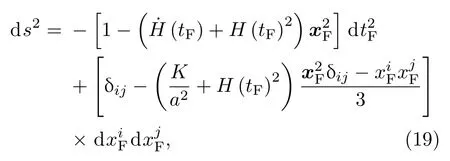
其中H是哈勃常数,这里得到的FNC也可以通过(12)–(14)式求出.特别地,里奇标量的空间分量可以容易写作
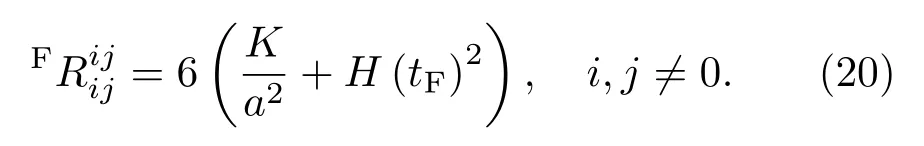
3 面积缺陷
首先,考虑d维时空在测地线中心O的FNC系,测地线从O发出正交于ua,形成一个d−1维类空球.假设l是球的半径,考虑一个基于O的FNC系,类时坐标类空坐标其中r是测地距离,ni是一个单位向量,满足δijninj=1,时空度规的号差取为(−+++).假设球的半径远小于局部曲率长度(即l≪H−1).Σ上空间度规gij在(14)式已经给出,Σ的FNC坐标的二阶体积元为
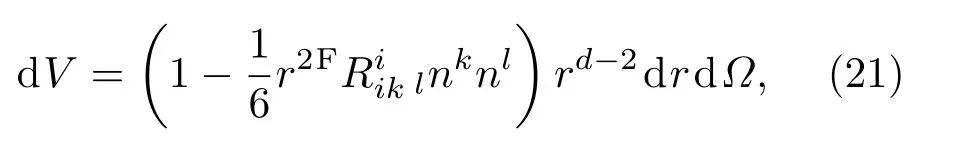
dΩ代表单位(d−2)球体上的面积微元.对于球对称函数从到积分
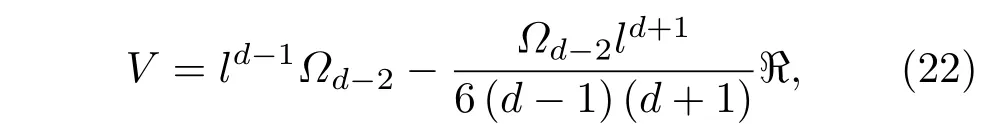
ℜ=的空间里奇标量,Ωd−2代表(d−2)球体上的面积.利用积分与闵可夫斯基空间在ℜ=0处相比,固定半径下的体积变化
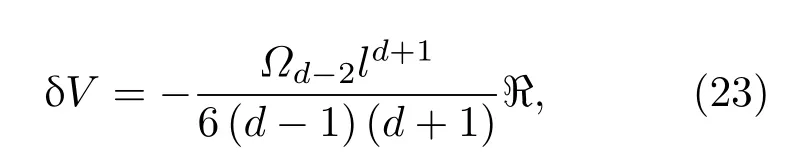
∂Σ面积变化由dδV/dl给出,即
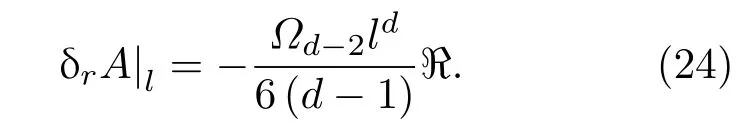
当球的半径变化时,体积和面积的变化形式为

总面积变化可分解为两部分,
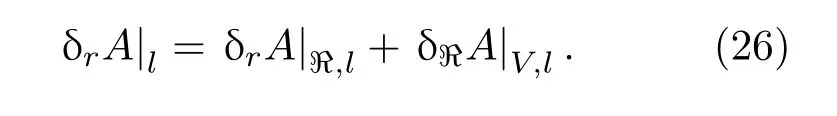
然后在固定体积的面积变化满足[7]
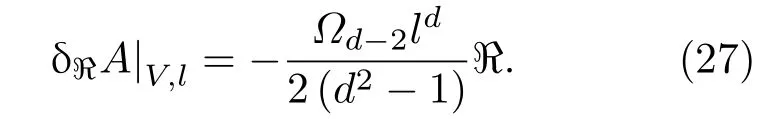
对于FLRW度规,空间里奇标量为ℜ=6(H2+k/a2).在本节中可以发现固定半径和固定体积下的面积变化,利用费米坐标中里奇标量等于两倍的一般爱因斯坦张量00分量可以联系到爱因斯坦方程.在文献[3]中,作者考虑了体积缺陷并从复杂性/体积对偶出发导出爱因斯坦方程.此外,他们发现宇宙加速膨胀可以理解为由量子复杂性造成的.
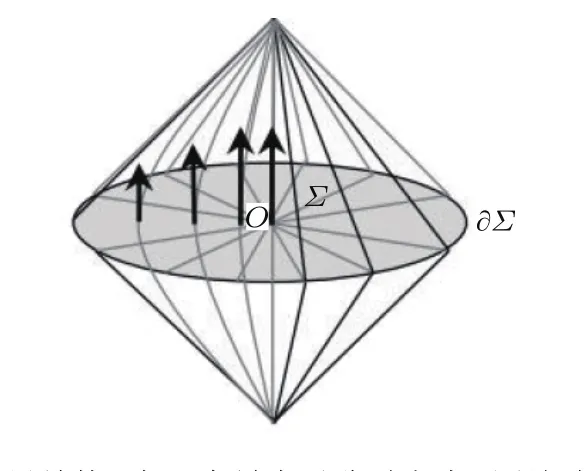
图1 因果结构,在一个最大对称时空中,测地球Σ的中心为O,边界为∂ΣFig.1.A sketched diagram for Causal diamond of a ball-shaped Σ region with center O and boundary ∂Σ.
4 因果结构
文献[7]讨论了因果结构D(Σ)和闵可夫斯基线元共形等距,由基林(Killing)矢量推导出了独特的球对称性因果结构共形等距
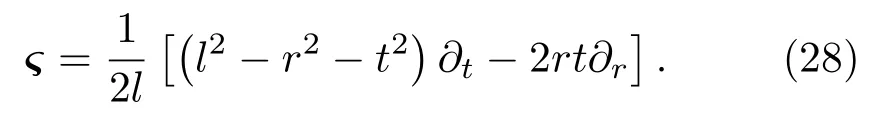
对于FLRW几何线元ds2=−dt2+a(t)2dx2,可以定义共形时间坐标
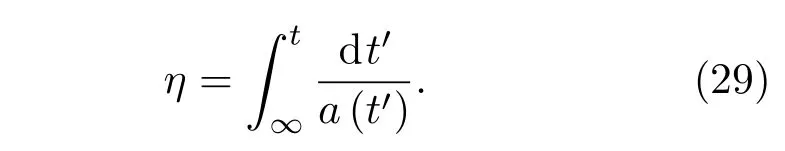
将度规变换为共形闵可夫斯基时空
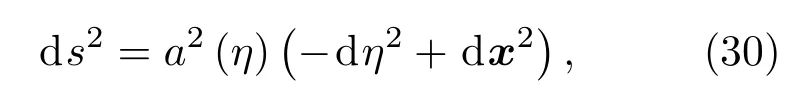
相应的基林矢量为
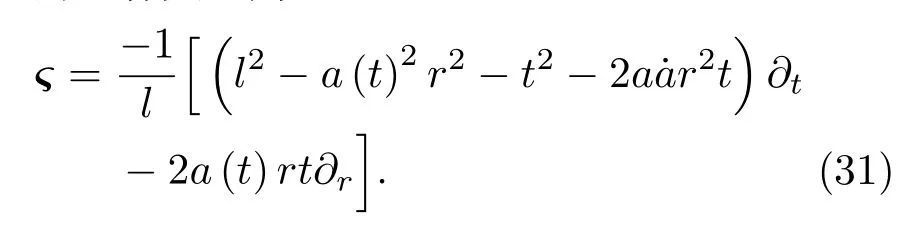
注意当a(t)=1,根据文献[7]可得相应的基林矢量
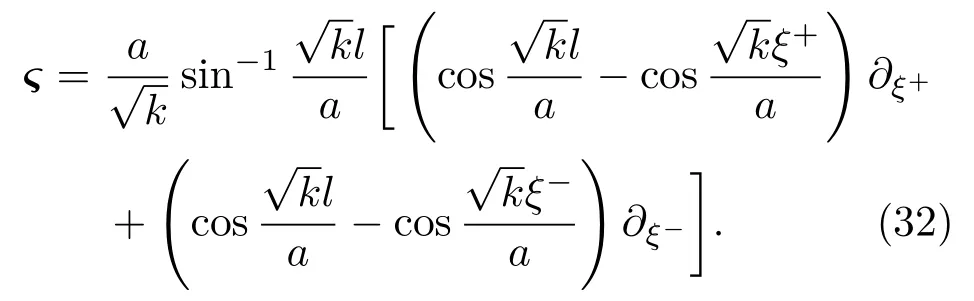
当k=0时基林矢量为
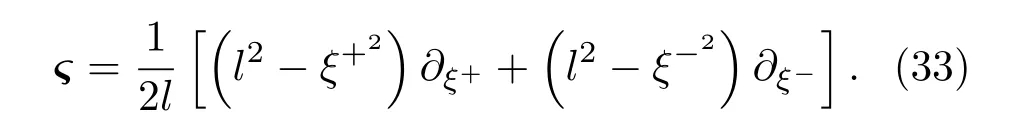
对于一般的在任意的空间曲率FLRW下ds2=度规取为下面的形式:
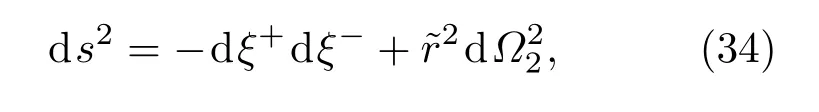
零坐标为
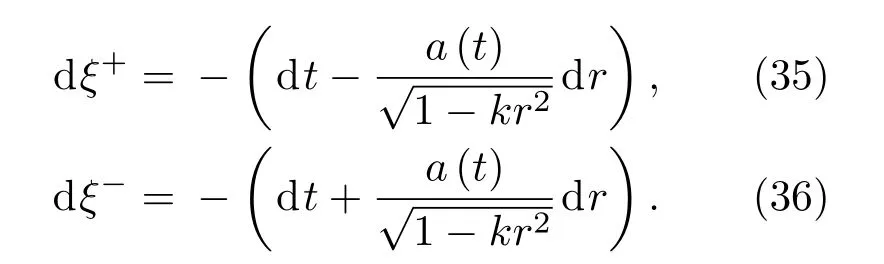
因此,基林矢量采取下面的形式
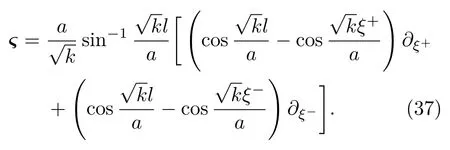
对于非共形物质系统,因果结构D(Σ)纠缠熵由紫外部分与红外部分组成.如果考虑几何的变化和量子场的状态,总熵变可以写成
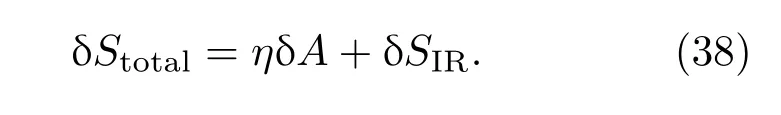
Jacobson在文献[7]提出最大真空纠缠假说:当几何和量子场由最大对称性同时变化时,在固定体积下小测地球中纠缠熵是最大的.由最大真空纠缠假说得
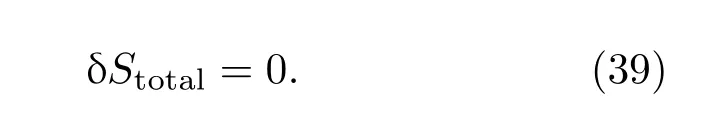
现在继续在最大真空纠缠假说下推导弗里德曼方程,分别在FNC和FNC系统中.
5 量子纠缠和弗里德曼方程
本节使用纠缠第一定律δSA= δ〈HA〉推导出宇宙学弗里德曼方程.现在假设因果结构封闭的量子态是热力学平衡的,第3节已经推导出了在固定体积下的面积变化.考虑处于平衡状态的普通热力学系统中的最小亥姆霍兹自由能F=E−TS,量子场理论的真空状态被限制在这个因果结构中可以表示成一个热密度矩阵:
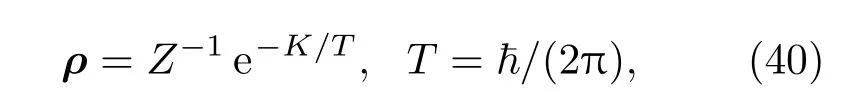
其中K与哈密顿量有关,T是Unruh温度[11,12],自由能FK= δ〈K〉−TS,δ〈K〉表示模哈密顿量的量子期望值,S=−Trρlnρ代表冯·诺依曼纠缠熵.由最小亥姆霍兹自由能原理知δFK必须为零,于是有
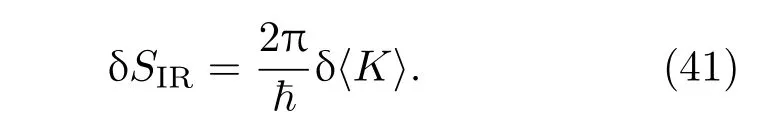
这是对于一个热状态的普通的克劳修斯关系,K和Hς在文献[7]中有比较详细的讨论.一般来说,这里的K不是一个局部算子,不生成几何流,对于普通的FLRW宇宙学,它与CFT无关.对于非共形物质场,文献[7]猜想中有附加项δX,
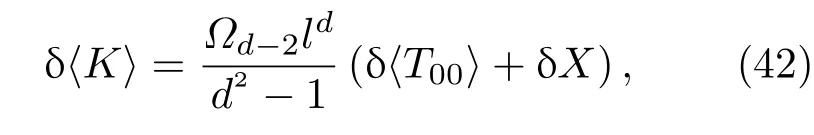
δ〈T00〉是能量密度的变化,δX是一个时空标量,X首次引入于文献[7],它在量子场理论中是一些标量运算符.下文只考D=4的特殊情况,假设量子场是具有因果关系的,处于热力学平衡状态且由真空态支配.在固定的体积下总熵变为0,即从(38),(41),(42)和(27)式可得
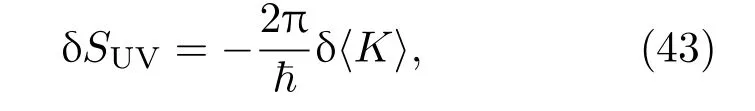
从而
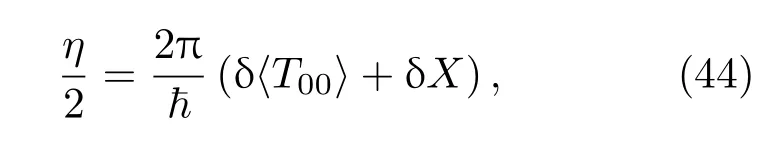
因此
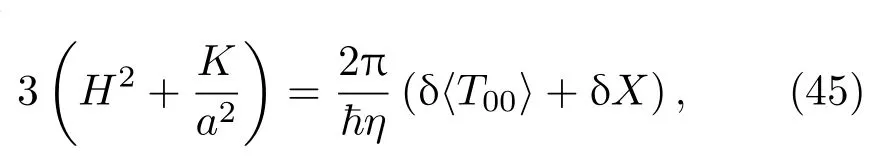
其中η=1/(4πG).下文假设δX=0,对于第一阶,假设宇宙不是空的而是由一些物质和能量支配的.这里选择用理想流体来模拟宇宙中的物质和能量,一个理想流体的能量动量张量可以写成
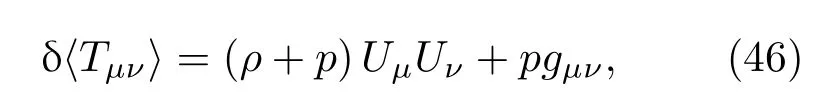
ρ是能量密度,P是压力,Uµ是流体的四速度,四速度Uµ=(1,0,0,0).能量动量张量可以简单表示成
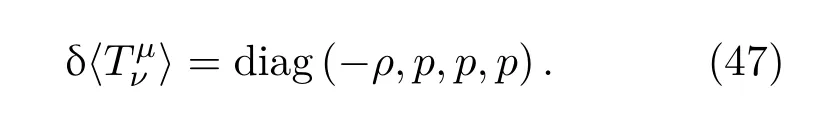
方程(45)重新写为标准的弗里德曼方程
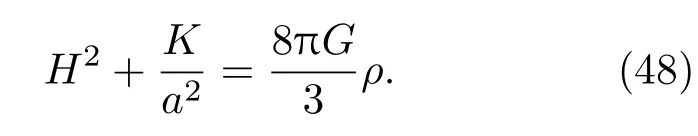
再加上理想流体的连续性方程
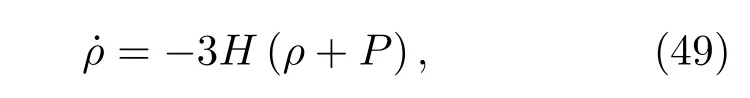
得出另外一个弗里德曼方程
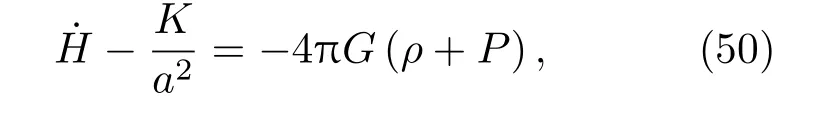
其中,·表示tF的导数.因此,对于FLRW宇宙应用纠缠第一定律得出弗里德曼方程.在这个意义上,弗里德曼方程的出现可以视为是由于物质δ〈HA〉纠缠的变化δSA的原因,推导的有效性仅限于一个小测地球的半径远小于视界半径,为了克服这个局限性,我们将在下一节探讨CFC.
6 共形费米坐标(CFC)和弗里德曼方程
现在讨论CFC的构建.为了研究宇宙学应用,作者在文献[9]中引入CFC,CFC在视界外也是有效的.与FNC类似的是它构建在一个类时中心测地线附近,在CFC系中,最低阶CFC度规是一个平坦的FLRW时空.度规取为下面的形式:
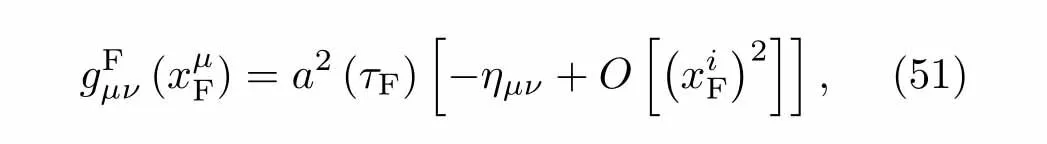
a(τF)代表共形时间,为了计算的方便引入共形度规下面简要介绍CFC的构建.
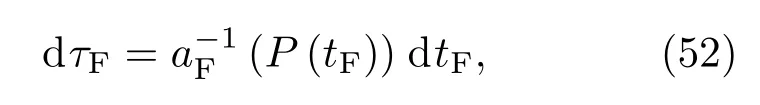
这里τF表示时间坐标,点P有CFC坐标(τF,0).考虑一族与有关的共形测地线通过条件分别得到P点的仿射参数和正切矢量.换句话说,αi通常决定测地线方向,λ测量共形度规测地线距离[9].P点在共形测地线上点的坐标为
于是可得CFC度规与共形黎曼曲率张量之间的关系:

Fikjl是黎曼曲率张量,在CFC系下的黎曼张量可以写作在全局坐标中可以计算出µναβ的分量.
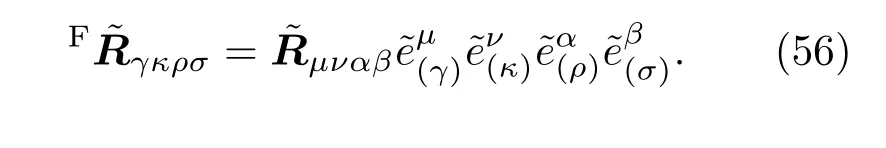
与第3节相似,考虑一个测地球,在真空纠缠熵是极值的条件下δStotal=0.通过类似于第5节的方法,在平坦宇宙中CFC系下弗里德曼方程如下:
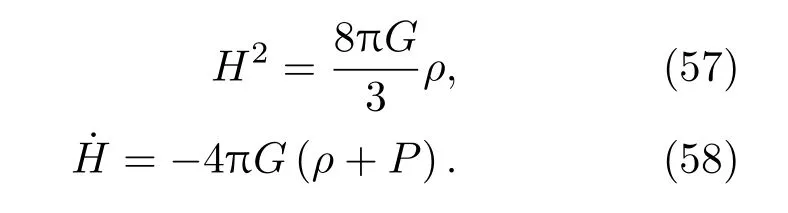
因此,得出FLRW宇宙下的弗里德曼方程在k=0的情况下是有效的.
7 讨论与结论
本文探讨了量子信息理论的关键概念与时空和引力之间的深层联系,在一个新的坐标系下研究宇宙学,认为时空几何是微观量子态的纠缠结构.结合理想流体的连续性方程从量子纠缠第一定律推导出宇宙学弗里德曼方程,讨论了时空微观自由度、纠缠与引力的关系.首先,在FNC下的因果结构尺度l比局部曲率长度小很多,但仍远远大于普朗克尺度lp的情况下推导出弗里德曼方程.如果因果结构尺度比得上紫外线尺度lp,那么量子引力效应就变得更强.通过探索CFC系统,我们拓展到一个更大的因果结构尺度进行讨论.在这个意义上,可以得到一个曲率修正值较高的引力场方程.
这里介绍的推导过程可以看作是一个弗里德曼方程导出的补充,这从宇宙学表观视界的热力学[13−15]可知.而如何从纠缠平衡态获得高阶导数引力下的弗里德曼方程,例如Gauss-Bonnet引力[16−18]和Lovelock引力[14,19],在这两种引力中,熵与视界面积的关系不再成正比,这时Gauss-Bonnet引力和Lovelock引力中的熵面积关系应该为表观视界的熵与面积关系.然后重复本文中的推导弗里德曼方程的整个过程,就能得出Gauss-Bonnet引力和Lovelock引力的弗里德曼方程.这可能涉及到纠缠第一定律的扩展,在此不做具体的推导.类似地,通过纠缠第一定律,文献[20–30]进行了一系列的计算,在均匀标量场的暴涨模型考虑弗里德曼方程将是很有趣的.对于纠缠的本质以及宇宙的评估的研究也会是一个有趣的课题[3].
量子纠缠可以用来描述量子物质态,对量子物质态中纠缠的大小的研究已经成为一个值得探讨的问题.而对纠缠结构面积定律的研究也有助于研究张量网络的算法[31],利用量子体系纠缠熵正比于其边界的大小为研究量子多体提供了可能.而有研究表明黑洞熵在某些方面也与面积定律有着深刻的联系[32].另外,从量子信息的角度来审视引力可以进一步促进我们对时空的本源的理解,从而更进一步地了解宇宙学.所以,量子纠缠的深远影响到底是什么,还需要我们去挖掘其中的奥秘.

