一种可用于极化3He实验的新型磁场系统∗

王文钊 胡碧涛 郑皓 屠小青 高朋林 闫松郭文传 闫海洋

1)(兰州大学核科学与技术学院,兰州 730000)2)(中国工程物理研究院核物理与化学研究所,绵阳 621900)(2018年3月30日收到;2018年5月25日收到修改稿)

1 引 言

近年来,极化3He气体被深入地研究并广泛地应用于各类科学实验之中.极化的3He气体可以作为等效的极化中子靶用来研究中子与带电粒子或光子的反应[1];极化的3He气体还可以用于探测超标准模型新的相互作用,譬如测量极化3He的核磁共振(NMR)频率的频移大小可以定量地探测自旋相关新的相互作用强度[2−4],而通过测量极化3He气体的弛豫时间可以研究速度相关的新相互作用[5];此外,极化的3He气体可以应用于磁强计[6,7]和核磁共振成像(MRI)[8]等领域;最后,因为极化3He原子核对中子的吸收截面与两者自旋取向的高度相关性,所以高度极化的3He气体也可以作为中子自旋过滤器用于中子极化和极化分析[9]等.目前,国内三大中子源CMRR,CARR,CSNS都在开展这种基于极化3He的中子极化及极化分析技术的研究.

线圈技术的进步是促进极化3He实验成熟的一个关键因素,均匀的磁场环境使得3He的极化率提高[10−12].极化3He实验中需要主磁场为3He提供极化方向.本文拟研究并改进极化3He实验中主磁场线圈的构型和参数,从而设计出能够满足纵向弛豫时间T1长达数百小时的小型3He极化装置,T1是一个自旋极化的系综回到热平衡态的平均时间.为了让极化3He的纵向弛豫时间长达数百小时以满足中子极化等应用的需求,需要3He气体所在区域的主磁场梯度小于10−4B0cm−1,其中B0是极化方向的主磁场强度.现有的3He实验中常用亥姆霍兹线圈提供主磁场,为了达到上述磁场均匀度,有些线圈的尺寸甚至达到了直径约1.5 m或以上;同时为了匹配后续电子学参数,要求3He所在区域的主磁场强度约为10 G(1 G=10−4T),需要约1000 A·匝的磁场线圈[13−15].已有的高均匀度的磁场构型例如马鞍形线圈[16],Merritt线圈等[17,18],比同尺寸的亥姆霍兹线圈均匀度高出一个数量级以上,使用这类线圈作为主磁场线圈,能有效地减小线圈尺寸.例如,对于通常尺寸(＜0.1 m×0.1 m×0.1 m)的3He容器,长度约为0.5 m、截面边长约为0.4 m的方形Merritt线圈可在容器所在区域内提供优于亥姆霍兹线圈的均匀磁场.我们已经完成了四正方形线圈的优化设计和实验实现.然而用于电子散射实验的3He容器,其气室长度可达40 cm[19],即使使用Merritt构型的磁场线圈,装置长度也将超过1 m.而马鞍形线圈较为复杂的线圈构型会增加线圈加工以及装配的难度.因此,本文设计出磁场均匀区域比例更大、结构较为简单的线圈构型.由于过于复杂的线圈构型会增加制造和装配的难度,综合考虑后,六线圈系统将是下一步较好的选择.此外,方形线圈具有移动放置方便、装配容易、无需外部支架等优势.综上,本文通过解析计算三组对称放置的等尺寸正方形线圈组产生的磁场大小,研究并优化其磁场梯度的空间分布,设计出了拥有大于30%的内部空间满足磁场梯度小于10−4B0cm−1的构型,为未来极化3He装置的小型化提供了条件.

2 方形线圈产生磁场的计算

2.1 弛豫时间与磁场梯度的关系

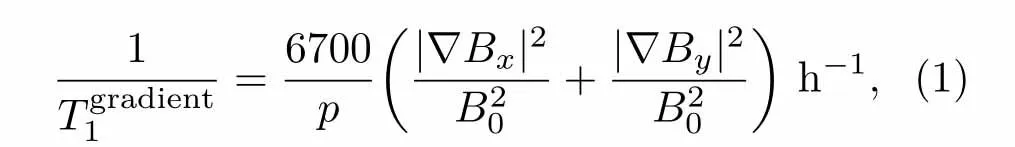
在3He气体极化的实验中,Tgradient1是由主磁场的梯度所造成的弛豫项,室温下其大小可以表示为[20]式中p为室温下的气体压强.假设3He的极化方向即主磁场的方向沿z轴,分别是磁场x和y方向分量的梯度,单位为cm−1;而B0是沿极化(z轴)方向的主磁场强度.从公式中可以看出,长的纵向退极化时间T1要求有尽可能小的磁场梯度而在方形线圈的情况下,主磁场方向沿z轴,Bx和By的空间分布具有正方形的旋转对称性,因此只需最小化即可同时使达到最小.因此我们设计一个如图1所示的新的六正方形线圈的磁场构型,在尽可能大的区域内使小于10−4cm−1,从而获得长的纵向弛豫时间T1.

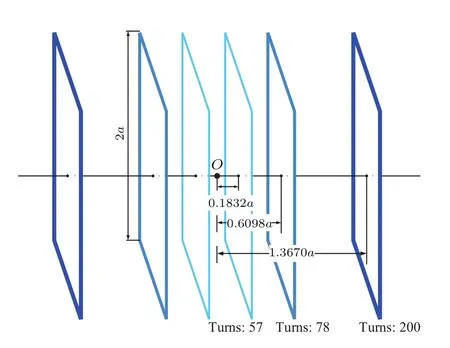
图1 六正方形线圈结构示意图Fig.1.Six square coils schematic.

2.2 单个正方形线圈产生的磁场

本文针对方形线圈组产生的磁场进行优化.图2所示方形线圈电流在空间任意点x(x,y,z)处产生的磁场大小可拆分为四段线段电流(分别为I12,I23,I34和I41)在该点处产生的磁场强度的矢量叠加.由毕奥-萨伐尔定理可知四段电流产生的磁场强度分别为:

µ0是真空中的磁导率,其中

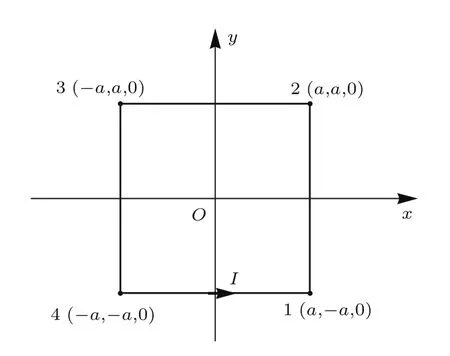
图2 方形电流磁场Fig.2.Square current magnetic field.

而

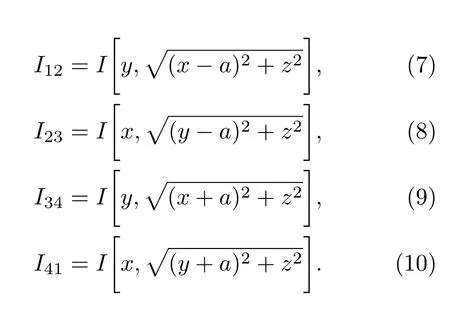
所以总磁场强度等于

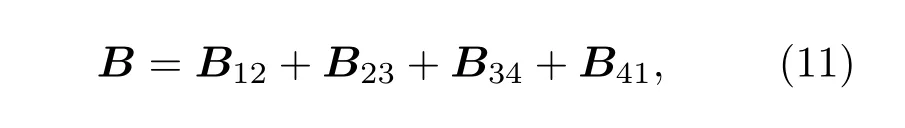
其中各分量的大小为

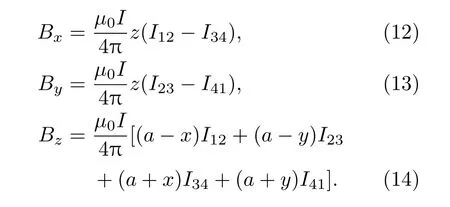
单个边长一半为a=1的正方形线圈通电流I后,其在极化方向上产生的主磁场强度B0=Bz(x,y,z),磁场方向沿z轴.磁场x方向分量Bx在全空间中的分布为

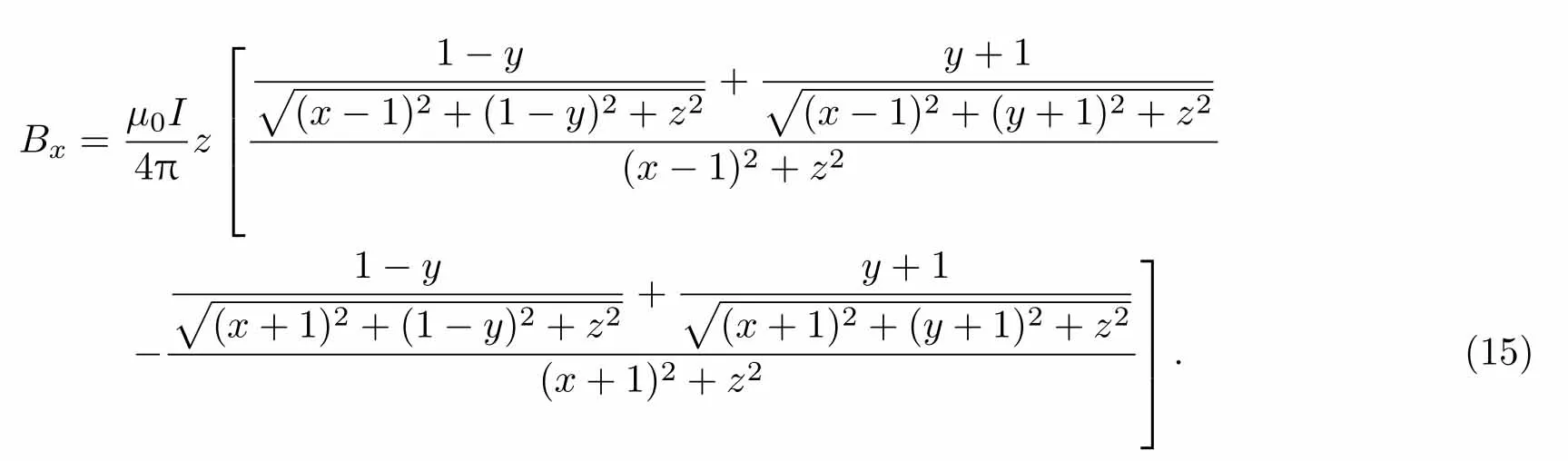
2.3 对称方形线圈产生的磁场

一般情况下,方形线圈产生的|∇Bx|2不为0且在空间中连续分布.为了得到高极化率的3He气体,需要让|∇Bx|2在尽量大的空间区域内趋近于0.考虑到实验中要求3He容器的尺寸小于线圈的大小(即x,y,z＜a),因此可将Bx的表达式展开为空间坐标x(y,z)/a的泰勒分布函数.通过调整线圈的构型,尽可能地让|∇Bx|2～0,以此来得到尽可能大的空间均匀区域.

同轴对称放置的相距为2d的方形线圈组(假设a=1),在其中心(即原点,对称轴为z轴)附近的Bx由(17)式可展开为

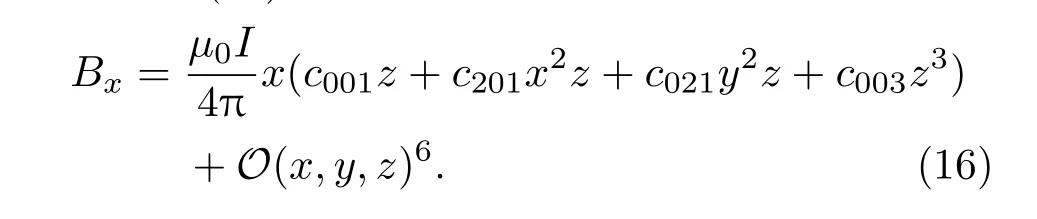
其中各项前的系数为:

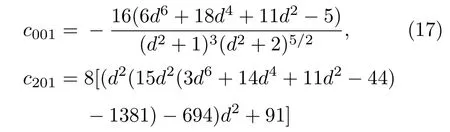
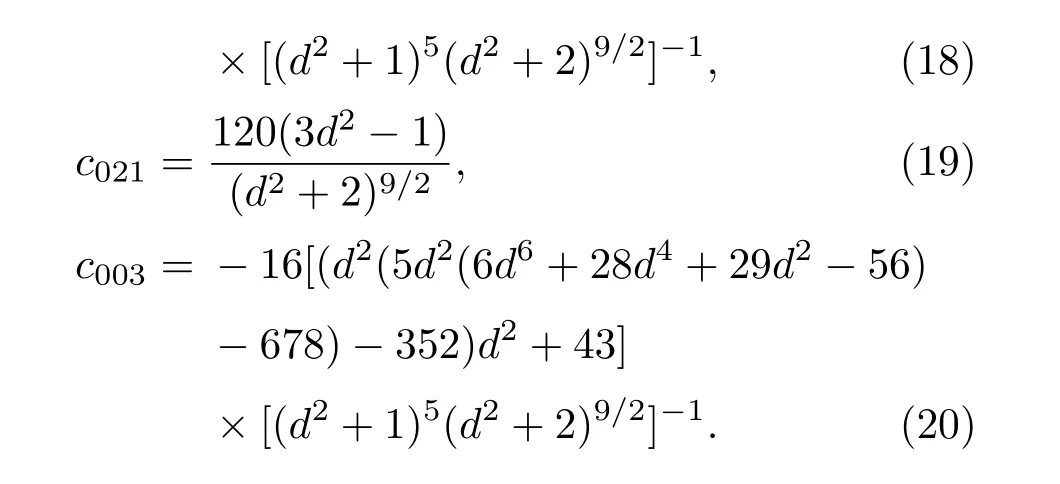
更高阶项的表达式见附录A.

上述磁场梯度的大小为

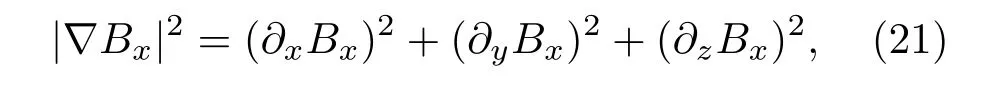
其中各导数项的表达式为:

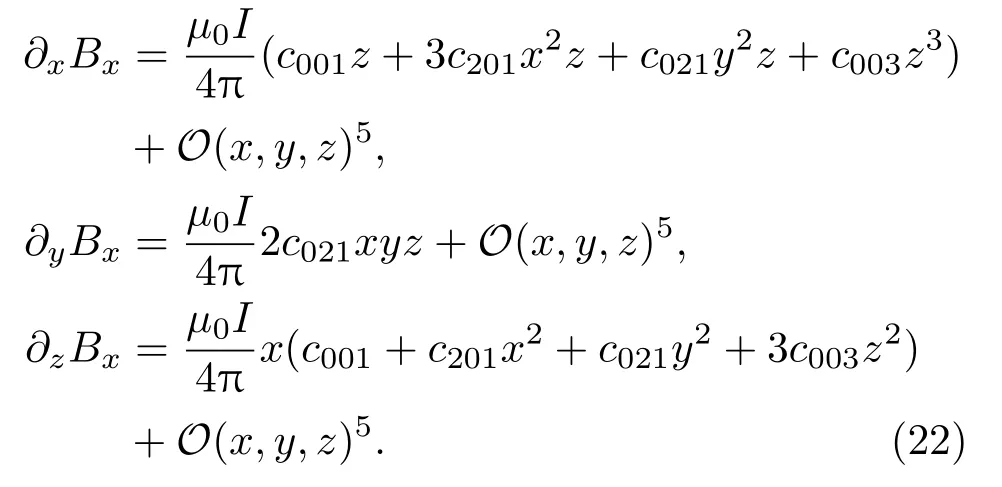
要优化线圈系统内部尽可能大的区域(x,y,z较大的区域),即使是x,y,z的高次项也不能看作小量.同时,为了保证在离中心较远的区域不会因为磁场分量Bx强度过大使磁场方向发生改变,需要Bx在线圈内部全空间尽量小,最好趋于0.由(18),(23),(24)式可以看出Bx与|∇Bx|2展开项包含的系数相同,优化Bx使得线圈内部所有Bx约为0,Bx在全空间内的梯度自然也小.因此只需调节线圈构型(例如间距d)使得各项前系数cijk尽可能小,在Bx约为0的同时就可以使得|∇Bx|2在空间中各点上都趋近于0.对于单组对称放置的线圈,可调参数只有线圈间间距d;而对于同轴放置的四线圈系统,可调参数增加为两组线圈的间距d1和d2以及两组线圈电流比I1/I2三项.但即使如此也不可能找到参数使c001,c201,c021,c003这四项系数同时等于零.不过可以通过调节d1,d2和I1/I2找到能使最小的参数压低|∇Bx|2的数值.

3 方形六线圈系统产生的磁场

3.1 参数优化

为了获得均匀区域更大的磁场构型,使得|∇Bx|2尽可能小,我们设计使用全同的方形六线圈系统来产生所需的磁场.系统由三组对称放置的线圈组构成,其产生的磁场大小Btx为三组线圈分别产生的磁场大小之和,即

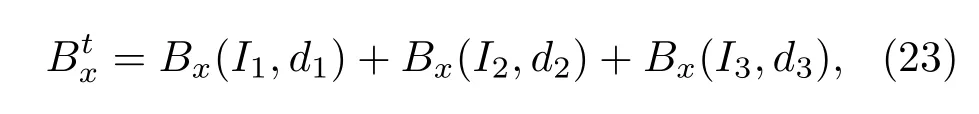
其中Bx由(16)式给出,2d1(2,3)和I1(2,3)分别是三组线圈之间的间距和三组线圈中通过的电流大小.因此将做泰勒展开后,各项系数的表达式变为:

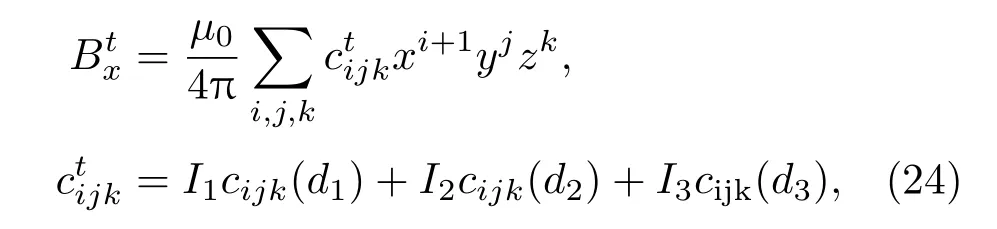
其中可调参数有d1,d2,d3,I2/I1,I3/I1共五个.

经计算后发现,展开Btx至x,y,z的八阶项后,调节d1,d2,d3,I2/I1,I3/I1使得最小的参数能够使线圈系统内|∇Bx|/B0＜10−4cm−1的均匀区域达到最大.此时磁场系统的具体参数如图1中所示,三组线圈到磁场中心的距离分别是其边长的0.6835,0.3049和0.0916倍,其上电流之比则为200:78:57.当正方形线圈边长为40 cm时,三组线圈到磁场中心的距离分别为27.34,12.20和3.66 cm.

3.2 线圈性能对比

为了更为直观地展示上述六线圈系统相比

Helmhotlz线圈构型拥有更大的均匀区域,分别在x,z两个方向上对比了截面大小相同的六线圈和Helmhotlz线圈满足a·10−4cm−1要求的磁场区域大小.

令正方形线圈的边长为2a,图3是当y=0时,x方向上均匀度满足a·10−4cm−1的磁场区间(阴影部分)随z/a变化的分布图.从图3中可以看出,新设计的六线圈磁场系统在所有位置都拥有比Helmhotlz构型更大的磁场区域满足条件a·10−4cm−1.在六线圈均匀区域的边缘位置x=0.58,y=0,z=0.01处,Bx/Bz=9×10−5,磁场方向几乎不会改变.

最后,图4展示了六线圈和Helmhotlz线圈产生的磁场中梯度轴上的分布图.从图4可以看出,在轴向上靠近中心区域的位置,六线圈磁场与Helmhotlz磁场有着相似的均匀度,但当|z/a|＞0.16时,Helmhotlz线圈产生的磁场梯度迅速增大,反之六线圈依然保有很好的均匀度.在z轴上,六线圈内部|z/a|＜0.917的区域内均满足a·10−4cm−1的要求,而对于Helmhotlz线圈,此区域仅为|z/a|＜0.

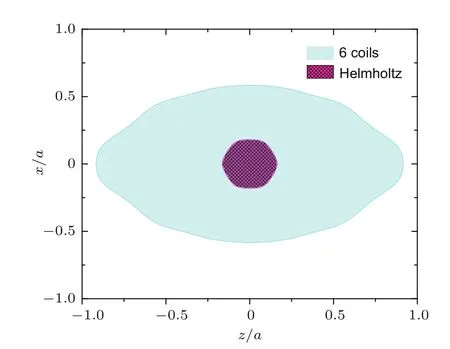
图3 16.区域在x-z平面(y=0)内的分布图 Fig.3.area within the x-z(y=0)plane.

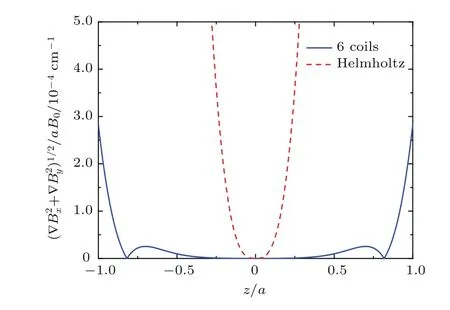
图4 在z轴上的分布图Fig.4. distributions on the z axis.

4 结 论

在以往的极化3He实验中,为了减少磁场梯度对纵向弛豫时间的影响,需要使用大尺寸的亥姆霍兹线圈来提供极化所需的主磁场.而小体积大均匀区域的磁场系统不仅更适于在线中子极化等应用,更为极化3He与电子散射实验等实验装置的小型化所必须.本文选用对称放置的等尺寸正方形六线圈系统为极化3He实验提供主磁场环境,通过解析计算线圈系统产生磁场的梯度在线圈内的空间分布,将磁场梯度泰勒展开为空间坐标x,y,z的幂指数函数并调节线圈的构型参数使得各展开项前的系数趋于最小,最终找到了能够适用于极化3He实验的线圈装置.其中,新的六线圈磁场由三组对称的全同线圈构成,各对线圈到磁场中心的距离分别是线圈边长的0.6835,0.3049和0.0916倍,其上通过的电流比为200:78:57.通过模拟计算后发现,六线圈产生的磁场在轴向上均匀度满足的区域达到了整个线圈长度的约70%;而在其他方向上六线圈内部约30%的空间区域均可用于极化3He实验,大小远超Helmhotlz等其他线圈系统.同时因为该磁场系统中心区域的高磁场均匀度以及磁场内部大的均匀区域,对于核磁共振实验、眼球运动精准测量实验等需求高均匀性磁场的实验研究有着很好的应用价值.

附录A

同轴对称放置的相距为2d的方形线圈组(假设a=1),将其中心(即原点)附近Bx的泰勒展开到第八项后表达式为

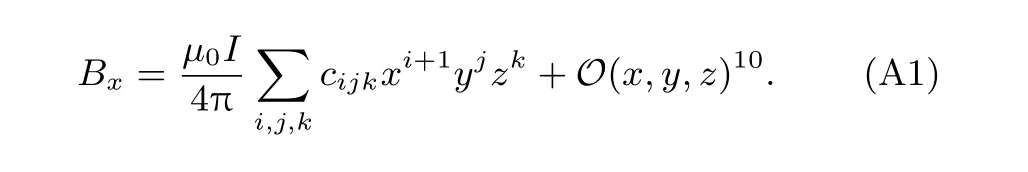
其中各项前的系数为: