Λ型三能级原子与两个谐振器的量子相位门∗

刘超 邬云文

(吉首大学物理与机电工程学院,吉首 416000)(2018年4月26日收到;2018年5月28日收到修改稿)

1 引 言

随着人类社会的发展,人们对信息的处理和传播提出了更高的要求,而传统的计算机终将不能满足需要,量子计算[1]和量子信息处理[2]能够通过量子力学的基本原理解决经典计算机难以甚至无法解决的算法问题,近年来引起了广泛关注.量子相位门是实现量子编码和量子计算所必备的量子组件,具有幺正性和可逆性的特点[3].

人们对量子相位门系统进行了广泛的研究,相继提出了各种理论方案[4−6],其中由微波谐振器和超导量子位组成的系统特别具有吸引力[7,8].超导量子比特(如磁通量子比特)具有相对长的去相干时间[9],可以使用电磁脉冲来改变Josephson(无耗散非线性电感器件)上的磁通量、电荷或相位差来控制其量子态[10],并且具有状态读出的各种单量子和多量子位操作能力[11,12].另一方面,远距离的量子位之间的相互作用耦合难以实现,而超导谐振器可以提供用作量子总线的量化腔场,实现量子总线在量子位之间分配量子信息[13−15].此外,微波腔和超导电荷量子位[16]或磁通量子位[17]之间的强耦合早在理论上就被推测并且已经被实验证明[18,19].

文献[20]提出了一种使用复杂的经典微波脉冲来控制两个超导谐振器的量子态方法,该方案需要提前准备两个初始态为Bell态的超导量子位,另外为了获得纯光子的任意量子状态,还需额外的技术将量子位与谐振器去耦合.而本文提出的由两个谐振器通过电容与一个Λ型三能级原子相耦合的方案,实验装置得到简化,这对减小器件之间的相干性很重要,另外,原则上我们的方案对于经典脉冲的强度没有限制,可以更快地进行操作.总体而言,我们的方案更加简单,能够有效提高相位门的保真度.

2 模型介绍

考虑由两个高质量超导谐振器和一个Λ型三能级原子耦合的量子系统,如图1所示.

图1 (a)量子相位门系统结构图;(b)Λ型三能级原子能级结构图Fig.1.(a)Quantum phase gate system structure diagram;(b)Λ-type three-level atom energy level structure diagram.

在这个模型中,量子相位门系统由两个高质量超导谐振器(ra和rb)通过电容与一个Λ型三能级原子c相耦合.通过调整谐振器频率,可以使谐振器与Λ型三能级原子c不同能级的相互作用,也可以通过改变施加到Λ型三能级原子c上的超导量子干涉仪(SQUID)的磁通量,来调整Λ型三能级原子

图1 (a)量子相位门系统结构图;(b)Λ型三能级原子能级结构图Fig.1.(a)Quantum phase gate system structure diagram;(b)Λ-type three-level atom energy level structure diagram.

在这个模型中,量子相位门系统由两个高质量超导谐振器(ra和rb)通过电容与一个Λ型三能级原子c相耦合.通过调整谐振器频率,可以使谐振器与Λ型三能级原子c不同能级的相互作用,也可以通过改变施加到Λ型三能级原子c上的超导量子干涉仪(SQUID)的磁通量,来调整Λ型三能级原子c能级间隔[21,22],使Λ型三能级原子c能级与不同谐振器的相互作用.图1(b)是Λ型三能级原子c的能级结构图,该Λ型三能级原子由基态|g〉c,第一激发态|e〉c和第二激发态|f〉c组成,是谐振器ra与Λ型三能级原子c的耦合强度,是谐振器rb与Λ型三能级原子c的耦合强度.在旋波近似下(ħ=1),系统哈密顿量为

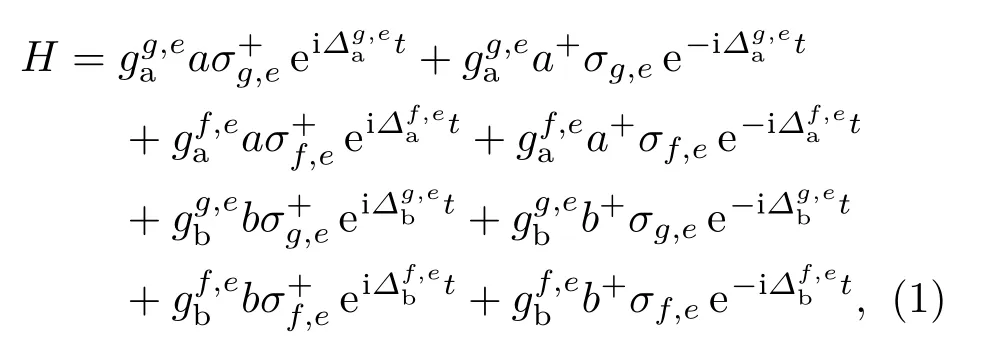
假设系统的一般初始状态为

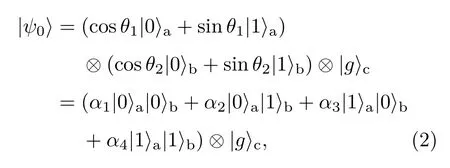
其 中|0〉a,|0〉b分 别 表 示 谐 振 器ra,rb的 量 子态;|g〉c表示Λ型三态粒子c的量子态;α1=cosθ1cosθ2,α2=cosθ1sinθ2,α3=sinθ1cosθ2,α4=sinθ1sinθ2. 这样无论θ1和θ2取任何值,都能保证系统的归一化.本文将两个归一化角度直接取为θ1=π/3,θ2=π/6,来对实现量子相位门可行性进行探讨.

3 量子相位门的实现

量子相位门的实现主要涉及谐振器ra与rb的开关和时间上的控制[23],以及调节SQUID的磁通量大小,使Λ型三能级原子c的某个确定跃迁能级与打开的谐振器跃迁能级相等,使其能级之间产生相互作用.两个量子相位门的实现详细描述如下.

3.1 Controlled-Z量子相位门

实现Controlled-Z量子相位门的步骤如下:

第一步,关闭谐振器rb,通过调整谐振器ra开关时间控制为使三能级原子在能级|g〉c和|e〉c之间转换,系统状态将演变成

第二步,关闭谐振器ra,通过调整谐振器rb开关时间控制为使三能级原子在能级之间转换,系统状态将演变成

第三步,关闭谐振器rb,通过调整谐振器ra开关时间控制为使三能级原子在能级|g〉c和|e〉c之间转换,系统状态将演变成

表1 实现Controlled-Z门的四种方法Table 1.Four ways to implement a Controlled-Z gate.

这只是我们所构建的Controlled-Z门操作的一种结果,同样,我们还有表1中的另外三种操作方法可以构成Controlled-Z门,而这三种方法对器件的调整,除开关时间外,都与Controlled-Z门方法的步骤相同.

3.2 Swap量子相位门

实现Swap量子相位门的步骤如下:

第一步,关闭谐振器rb,通过调整谐振器ra开关时间控制为使三能级原子在能级之间转换,系统状态将演变成

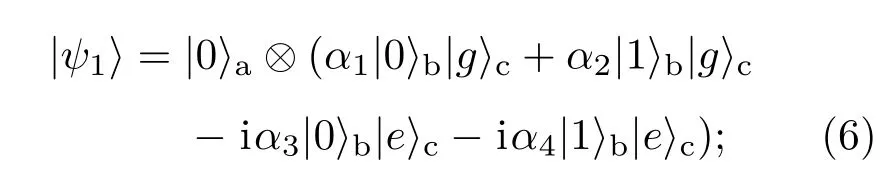
第二步,关闭谐振器ra,通过调整谐振器rb开关时间控制为和ωb=ωg,e,使三能级原子在能级|g〉c和|e〉c之间转换,系统状态将演变成

第三步,关闭谐振器ra,通过调整谐振器rb开关时间控制为和ωb=ωe,f,使三能级原子在能级|e〉c和|f〉c之间转换,系统状态将演变成

第四步,关闭谐振器rb,通过调整谐振器ra开关时间控制为和使三能级原子在能级|g〉c和|e〉c之间转换,系统状态将演变成

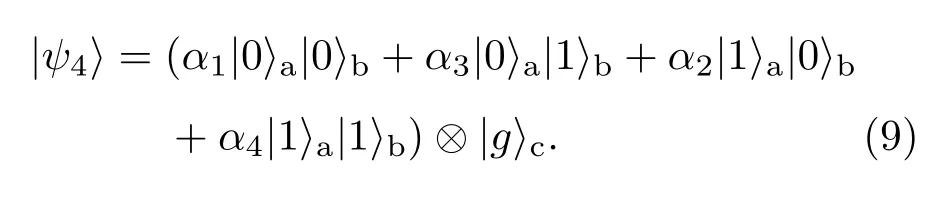
这只是我们所构建的Swap门操作的一种结果,同样,我们还有表2中的另外一种操作方法可以构成Swap门,而第二种方法对器件的调整,除开关时间外,都与上述Swap门方法的步骤相同.

表2 实现Swap门的两种方法Table 2.Two ways to implement a Swap gate.

4 保真度

系统保真度对研究系统的可行性而言是一个非常重要的参量,为了展示我们所构建的两个量子相位门的可行性,我们利用可行的经验参数和数值模拟的方法,来对其中Controlled-Z门中的第一种方法进行保真度的计算和运行时间的确定.由这两个谐振器和Λ型三能级原子c组成的系统随时间演变可以由如下Lindblad主方程描述[24,25]:

在这个Lindblad主方程中,L[Λ]=(2ΛρΛ+−Λ+Λρ − ρΛ+Λ)/2,其中σee=|e〉c〈e|;σff=|f〉c〈f|. 方程第一项引用(1)式,−i[H,ρ]是密度算符ρ所遵循的基本运动方程项;κa,κb分别是谐振器ra和rb的衰减率;rg,e,rf,e分别是关于Λ型三能级原子c能级变化的弛豫速率;rϕ,e和rϕ,f分别是Λ型三能级原子c能级|e〉和|f〉的移相比率.主方程后面的几项组成了这个系统的衰减项.

对于三能级原子,调节范围在0.1—1.0 GHz之间的电荷耦合强度已在实验中实现[26,27].这里通过调整SQUID的磁通量来改变Λ型三能级原子c的能级差,使在第一步和第三步中ωa=ωg,e,达到谐振器ra与指定能级间|g〉c↔|e〉c相互作用的目的,第二步中ωb=ωf,e,达到谐振器rb与能级|f〉c↔|e〉c相互作用的目的.

通过对密度算符ρ所遵循的运动方程的计算,将量子相位门的保真度定义为如下方程:

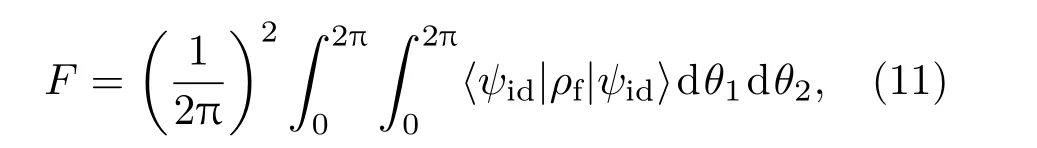
这里[1/(2π)]2为归一化系数;|ψid〉是在不考虑任何衰减的情况下,从初始态|ψ0〉到最终实现量子相位门的理想态,对于我们所讨论的Controlled-Z门而言,即是(5)式的|ψ3〉;ρf是在含衰减的情况下,通过Controlled-Z门三个步骤的实际运行操作后得到整个系统的最终密度算子.对Controlled-Z门方法一的仿真表明,通过总时间为20.83 ns的运行操作,其保真度为96.67%,达到了实际可应用的水平.

不同参数对量子相位门保真度的影响如图2所示,改变衰减率κ,弛豫速率r,移相比率rϕ或耦合强度g其中一个参数,其他参数固定为前文所使用的数值模拟参数.由于图2(a)—(c)的横坐标都为x−1,所以随着衰减率、弛豫速率和移相比率的增加,保真度随之降低,呈负相关性,但影响程度明显不一样;图2(d)中,随着耦合强度g的增加,保真度也随之增加,这是由于增大的耦合强度会使作用时间缩短,从而减小衰减项的作用时间,使得保真度增加.

图2 四个参数对实现方法一Controlled-Z门保真度的影响Fig.2.In fluence of four parameters on the fidelity of a controlled-Z gate:

5 结 论

通过构建由两个超导谐振器和一个Λ型三能级原子组成的量子相位门系统,提出了用以实现Controlled-Z门和Swap门的简单操作方案,并利用数值模拟参数对实现Controlled-Z门的第一种方案进行了仿真,探讨了各参数对其保真度的影响.结果表明该方案是可行的.系统三个衰减参数衰减率κ、弛豫速率r、移相比率rϕ的增大会减小保真度,而耦合强度g的增大会缩短相位门的运行时间,从而减小衰减参数的作用时间,使得保真度增加.我们希望在今后的研究中能够找到更加有效简单的操作方法,同时也期待提出的方案能够激励这方面的实验研究,使更多的研究人员致力于量子相位门系统的研究.