运用变式教学培养高中生的数学学科核心素养

荣成市第二中学 宋传凤 赵洪新

数学学科核心素养是在高中数学新课程标准中提出的新概念：具有数学基本特征的适应个人终身发展和社会发展需要的人的数学品质和数学关键能力。与旧的课程标准相比，数学学科核心素养是在“四基”与“三维目标”的基础上的继承与发展，更加重视个体的健全发展和对未来社会生活的适应能力，强调“数学思维”是数学学科核心素养的重要成分。

本文以人教B版数学选修2-1第二章《圆锥曲线和方程》的几个变式教学为例，感受变式教学带来的精彩。

一、用变式深化概念，做到领悟本质

教材中首先通过实例和实验，让学生探究椭圆的定义。对椭圆产生感性的认识。在这里，我们可以设置以下两个变式：

绳长大于两定点之间的距离时，轨迹是椭圆。变式1 绳长等于两定点之间的距离时，轨迹是什么？变式2 绳长小于两定点之间的距离时，轨迹是什么？通过这一组变式，让学生自己动手改变绳长，重新作图，通过观察与思考，得出问题的结论，并理解椭圆定义的本质。

在我们总结椭圆定义时，关于椭圆的表达方式，又有了下面的变式：

变式2：（图形表述）

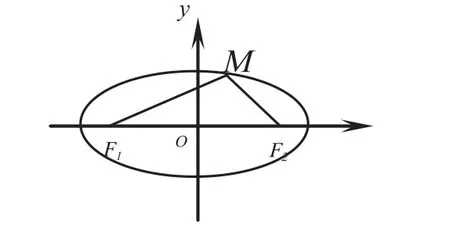
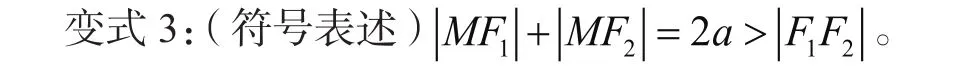
通过三种变式，帮助学生灵活转化条件，构建三者之间的关系，在解决相对复杂的椭圆几何问题上非常有效。

二、用变式激活思维，做到学以致用

在课本的第28页，有这样一道题：

（一）解题思路变式

一题多解，能启发和引导学生从不同的角度、不同思路，运用不同的方法和运算过程，解决同一道数学问题。教学中积极、适当地进行一题多解的训练，有利于激活学生的思维，开拓学生思路，促进学生知识和智慧的增长。

（二）不同角度变式

根据教材中的典型题，启发学生将命题的条件进行变化，引出与原题相仿的新题，或当命题的条件不变时，命题的结论从不同的角度进行联想、演变、引申，这样的变式训练，使学生由浅入深地研究问题，激活思维，做到学以致用，增强学生学习数学的兴趣，为高效课堂创造条件。

三、用变式发散思维，做到触类旁通

从茫茫“题海”中精选有思维价值的典型题，结合学生特点和已经掌握知识的程度进行变式练习，这样可以避免机械传授、表面化解决，可以培养学生的认识能力，扩大学生视野，开发学生的想象能力，深化知识，举一反三，触类旁通，有利于培养学生发散思维和灵活运用所学知识解决数学问题的能力。

四、用变式创新思维，做到高屋建瓴

（一）人教B版选修2-1 第70页的练习A第3题是这

波利亚认为，数学教育应培养学生的“独立性、能动性和创新精神”，这道题和它的三个变式，从特殊到一般，从静态到动态，源于课本又高于课本，在本题的分析过程中，学生可以独立地设计、发现和解决变式问题。

通过这种对一个典型题的层层推进，不断变式，深入展开探究，引导学生深入思考，使学生学一道题会一类题，有助于学生掌握解决这个问题的规律，掌握数学问题设计的基本结构，并使原有孤立的零碎的知识整体化，促进对知识块整体的认知，得到解决问题的创新性思维。

（二）圆锥曲线的定义、方程和性质，无不体现着代数形式和几何形式的和谐统一，其中存在的诸多与垂直有关的定值问题也绝非偶然，这是由圆锥曲线的定义及特性所决定的，这一类问题在教材中也是有“本”可“变”。

过抛物线的顶点O 作互相垂直的弦OA和OB。求证：弦AB 与抛物线的对称轴相交于定点。

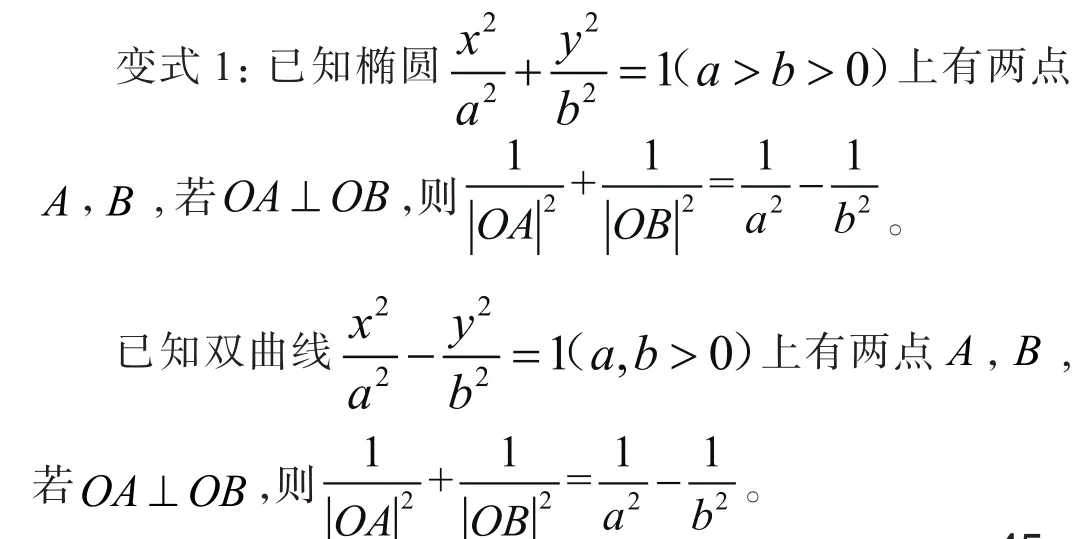
变式教学使一题多用，多题重组，给人一种新鲜、生动的感觉，能唤起学生的好奇心和求知欲，掌握问题的发展规律，使学生对数学知识从感性上升到理性的层面，培养学生的数学意识和思维的深刻性、创造性。一道题通过变式，从不同角度将已学过的知识加以复习，强化知识的交汇，将知识能力和思想方法在更多的新情境、更高的层次中不断地交叉渗透，达到了对问题本质的再认识、再深化乃至升华的效果。

数学教学的本质就是展示和发展思维过程，这一思维过程就是对数学知识和方法形成规律性的理论认识过程。在数学教学中，教师借题进行多角度变式的思考与发散，不仅可以拓宽、优化学生的解题思路，培养学生思维的多向性、独立性和创造性，而且可以使学生对所学知识融会贯通、串珠成线，以达到“以少胜多”的学习效果。这样的变式教学有利于学生不断地总结、再思考，以取得对知识和方法的深入认识。长期进行下去，学生的创新思维和能力必然得到更高层次的提升，思考问题高屋建瓴，解决问题游刃有余。