高中数学齐次式的运用种种

江苏省泰州市第二中学 季礼萍

总会有学生存在疑问，为什么课堂上我听得懂，却考不了好成绩？有些数学老师上课常说学数学要有“悟性”，何谓悟性？

美国著名心理学家布鲁纳说：“不论我们选教什么学科,务必使学生理解该学科的基本结构。”而所谓基本结构是指“基本的、统一的观点,或者是一般的、基本的原理”，即掌握知识的“通解通性”。具体到数学教学中,就是要掌握贯穿在数学学科中的基本数学思想方法。

在数学教学过程中，教师应注意挖掘和提炼知识的发生、发展及应用过程中所蕴含的思想方法。下面我来举几个例子让大家体会一下齐次式是如何创造出来的以及有了齐次式如何求解最值问题。

一、在三角函数部分求最值

二、在等式条件下求代数式最值

三、在不等式恒成立条件下求参数最值

点评：这类问题在试卷中属于中上难度题，难点在于如何巧妙处理成三次齐次式，变式由正弦定理角化边不难，难点在分离参数后，右边本来就是二次式的比，怎样做到将三元变为二元，转化为可求最值的二次齐次式的比。

四、在向量问题中求最值

五、在解析几何问题中求定值

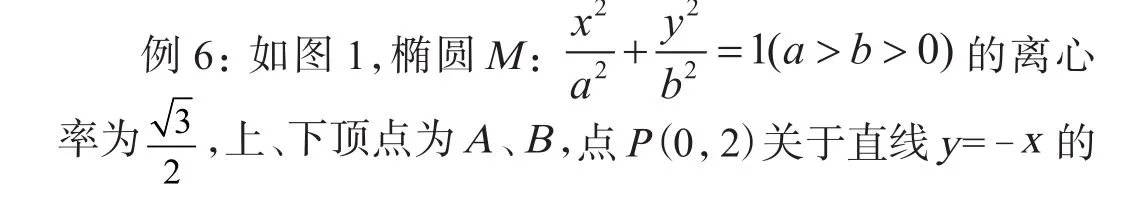
对称点在椭圆M上，过点P的直线l与椭圆M相交于两个不同的点C、D（C在线段PD之间）。

（1）求椭圆M的方程；

（3）当AD与BC相交于点Q时，试问：点Q的纵坐标是否为定值？若是，求出该定值；若不是，请说明理由。

图1

点评：借助韦达定理，寻求“积与和的倍数关系”，“消积留和”，巧妙转化为一次齐次式的比。

上述几个例子在近几年各地模拟试题中多是学生感到棘手的，但通过一些巧妙处理，我们都得到了一次、二次至多三次齐次式的比，使问题得以解决。在今后的教学和学习中需要对转化齐次式重视起来。

由此看来，我们不仅要关注到图形的对称美，还要感受到一些数学式子的齐次美。数学美育是数学教学的重要内容之一，在中学数学教学中渗透美育，能激发学生求知的兴趣，启迪学生积极思维，有助于学生深刻理解知识，对于培养学生健康的审美观念和审美能力，陶冶高尚的道德情操，培养全面发展的人才，具有重要作用。