Fuzzifying拓扑空间中的强半分离性
杨文华
内蒙古财经大学 统计与数学学院,呼和浩特 010020
1 引言
1991年,文献[1]提出I-Fuzzy拓扑概念的同时也提出了I-Fuzzy拓扑的特殊情形——不分明化(Fuzzifying)拓扑的概念,并且文献[1-3]用连续值逻辑LΝ1语义的方法建立了Fuzzifying拓扑学的基本理论。
自从Fuzzifying拓扑基本理论引入之后,就引起了国内外学者的广泛关注,并且相继做了许多有意义的研究,如文献[4-14]等。其中,文献[4]讨论了分离性问题;文献[5]研究了S-分离性;文献[6]利用Fuzzifying半开集、Fuzzifying半邻域和Fuzzifying半闭包导入了一种新的分离公理;文献[7]以预开集为工具引入了预分离公理;文献[8]以正则开集、R-邻域及δ-闭包为工具导入了几乎分离公理;文献[10]引入了拟R0分离公理。
文献[15]利用文献[16]中所定义的一种新的较为合理的半开集给出了Fuzzifying拓扑空间中的强半开集、强半邻域、强半闭包和强半内部等概念。本文将运用连续值逻辑LΝ1语义的方法,在Fuzzifying拓扑空间中以强半开集、强半邻域、强半闭包和强半内部为工具引入强半分离公理SPTi(i=0,1,2,3,4),并且深入讨论它们的性质及彼此间的关系。
2 预备知识
本文中,I=[0,1],X是非空集合,A⊂X,Ac=X-A。
首先,列出在本文中经常使用的关于模糊逻辑(赋值格为Lukasiewicz单位区间的逻辑)的一些记号。
对任意公式φ,符号[φ]表示φ的真值,这时真值集是[0,1]。一个公式φ为重言式,记作⊧φ当且仅当[φ]=1 。
(1)[α]:=α(α∈[0,1])

(2)若 A∈2X,则[x∈A]:=A(x)。
(3)若 X 是论域,则[∀xφ(x)]:=infx∈X[φ(x)]。
此外,相应的导出公式有:
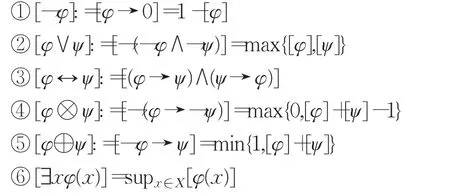
⑦若∀A,B∈2X,则:

其次,给出本文中经常使用的一些概念及定理。
定义1[1]若映射τ:2X→I满足以下条件:
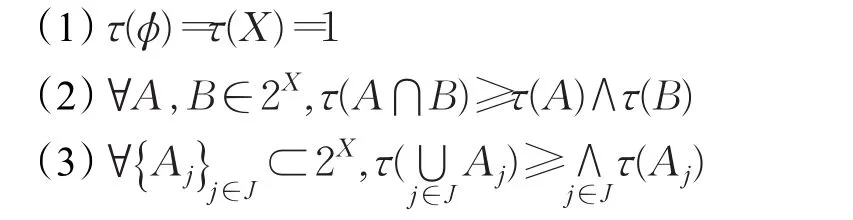
则称(X,τ)是Fuzzifying拓扑空间,一元模糊谓词τ称为X上的Fuzzifying拓扑。
定义2[16]设(X,τ)是Fuzzifying拓扑空间。
(1)定义一元模糊谓词 Sτ:2X→I如下,称 Sτ为Fuzzifying半开集。∀A∈2X

(2)定义一元模糊谓词SCτ:2X→I如下,称SCτ为Fuzzifying半闭集。
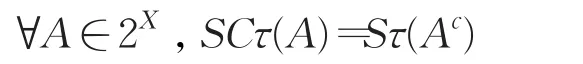
(3)∀x∈X,定义一元模糊谓词Sx:2X→I如下,称Sx为x的Fuzzifying半邻域系。

定义3[15]设(X,τ)是Fuzzifying拓扑空间。A∈2X,int(A)、cl(A)、ints(A)、cls(A)分别表示 Fuzzifying拓扑下A的内部、闭包、半内部、半闭包。
(1)定义一元模糊谓词SPτ:2X→I如下,称SPτ为Fuzzifying强半开集。

其中
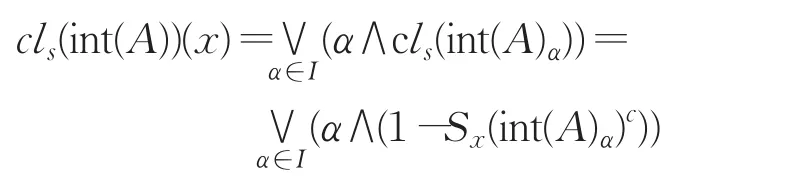
(2)定义一元模糊谓词SPCτ:2X→I如下,称SPCτ为Fuzzifying强半闭集。

(3)∀x∈X,定义一元模糊谓词SPNx:2X→I如下,称SPNx为x的Fuzzifying强半邻域系。

定义4[15]设 (X,τ)是 Fuzzifying拓扑空间,∀A∈2X,A的强半闭包记作SPcl(A),定义为SPcl(A)(x)=1-SPNx(Ac);A的强半内部记作SPint(A),定义为SPint(A)(x)=SPNx(A)。
定理1[15]设(X,τ)是Fuzzifying拓扑空间,则:
(1)SPτ(X)=SPτ(ϕ)=1
定理2[15]设(X,τ)是Fuzzifying拓扑空间,∀A,B∈2X,则:

3 强半分离公理及其等价刻画
定义5设Ω是所有Fuzzifying拓扑空间类,一元模糊谓词SPT0,SPT1,SPT2,SPT3,SPT4∈IΩ分别定义如下:
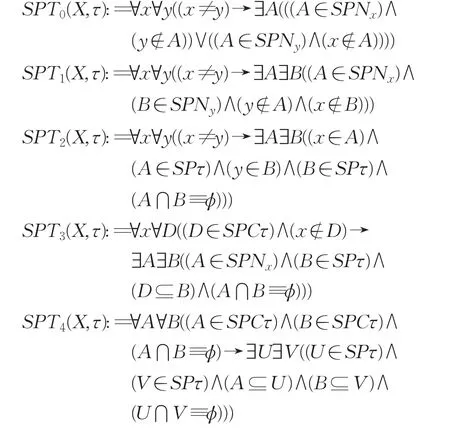
定理3设(X,τ)是Fuzzifying拓扑空间,则
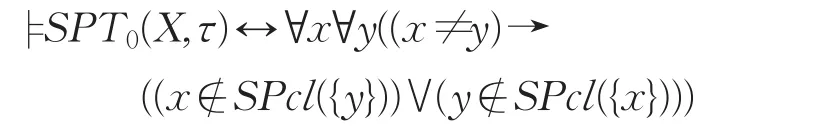
证明

定理4设(X,τ)是Fuzzifying拓扑空间,则
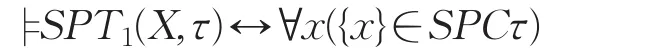
证明由定义3及定理2(2)知:

另一方面:

类似的
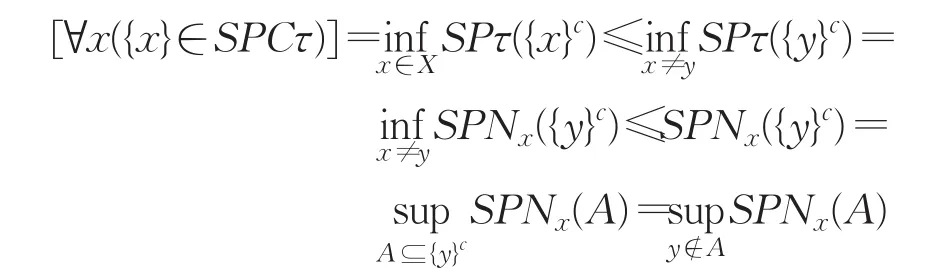
所以

定理5设(X,τ)是Fuzzifying拓扑空间,则

证明

定理6设(X,τ)是Fuzzifying拓扑空间,令
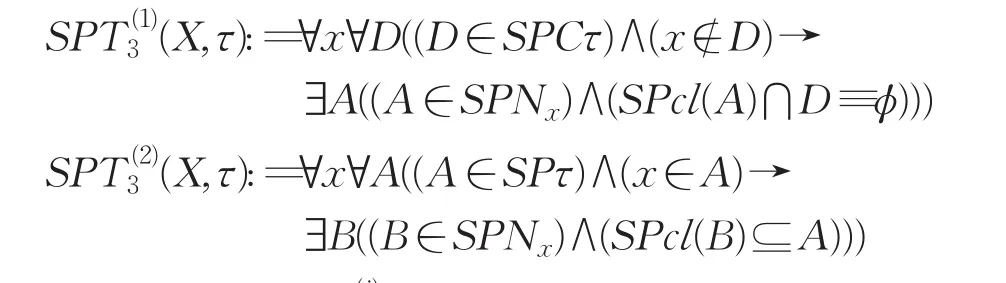
证明首先证明


只需证明下面的等式成立:


下证



综上

所以

定理7设(X,τ)是Fuzzifying拓扑空间,令

证明首先证明
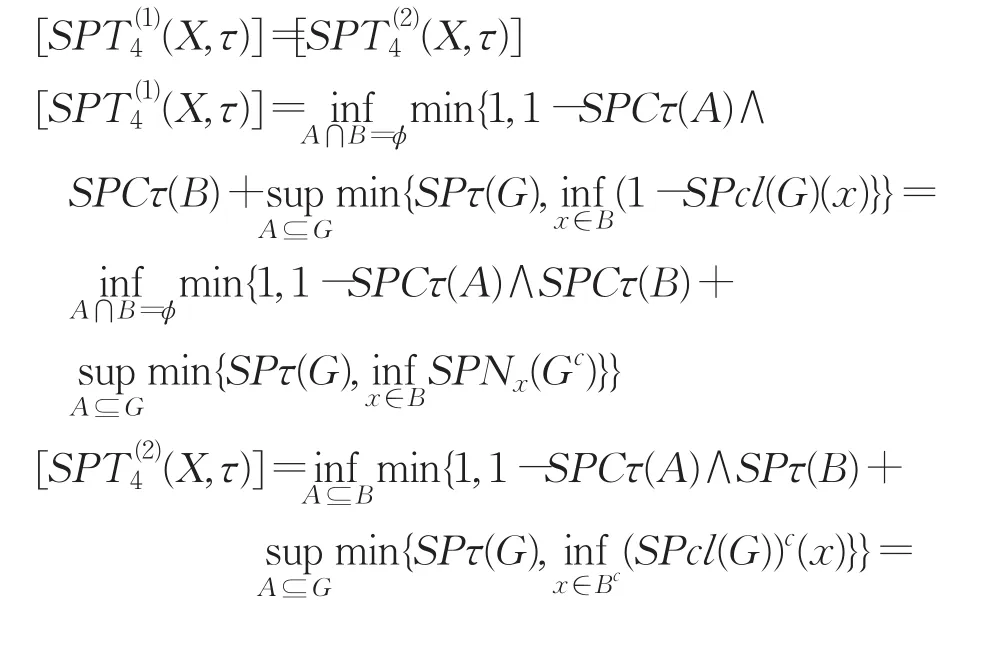

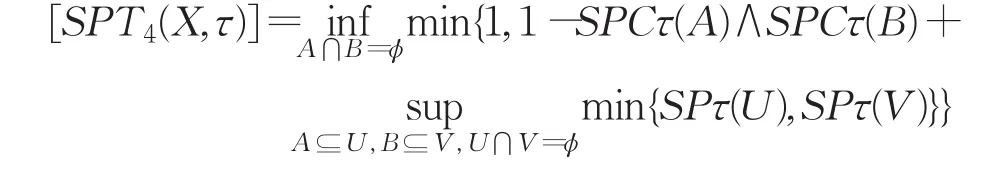
只需证明下面的等式即可:


4 强半分离公理间的关系
定理8设(X,τ)是Fuzzifying拓扑空间,则

证明(1)需证。因为

所以

(2)需证[SPT2(X,τ)]≤[SPT1(X,τ)]。因为当时,SPNx(A)=0;当时,SPNy(B)=0,故
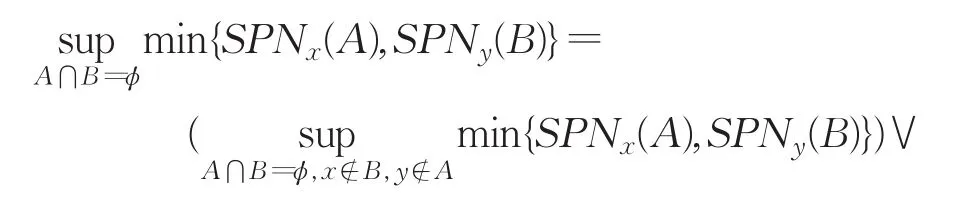

所以
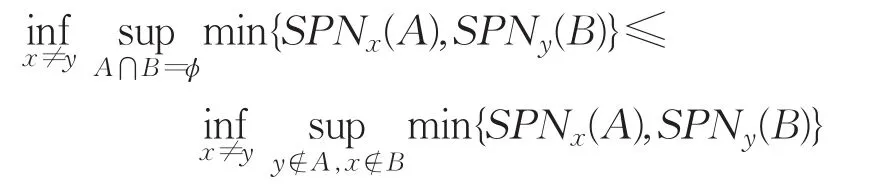
即 [SPT2(X,τ)]≤[SPT1(X,τ)]。
(3)由(1)、(2)可知:
引理1 ∀α,β∈[0,1],则

证明分α≤β及α>β两种情况讨论,易证。
定理9设(X,τ)是Fuzzifying拓扑空间,则

证明只需证明

由定理4知:

于是

又由于[SPT2(X,τ)]≥0,所以

定理10设(X,τ)是Fuzzifying拓扑空间,则

证明只需证明

即 [SPT3(X,τ)]≥[SPT4(X,τ)]+[SPT1(X,τ)]-1 。又由于[SPT3(X,τ)]≥0 ,所以
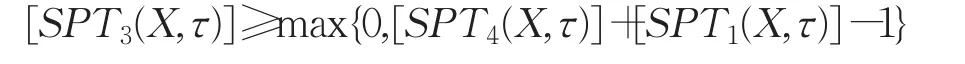
5 结论
本文主要在Fuzzifying拓扑框架下引入了强半分离公理SPTi(i=0,1,2,3,4),给出了各自的等价刻画以及它们彼此间的关系。文中运用了连续值逻辑LΝ1语义的方法,所涉及到的赋值格为Lukasiewicz单位区间,它是一个MV代数,所以这里就可以提出一个问题:能否将赋值格[0,1]推广到MV代数,甚至是正则剩余格。一方面,推广赋值格[0,1],那么拓扑框架也相应变得更广泛,在这个更广泛的拓扑框架下研究强半分离公理,那就需要相应一系列的研究基础;另一方面,Lukasiewicz单位区间是一个特别的MV代数,如果推广成一般的MV代数或正则剩余格,无疑会更加的复杂,所以这个问题能否解决还有待研究,可以作为一个思考方向。
——论胡好对逻辑谓词的误读

