圆锥曲线中两垂直焦点弦的若干结论

☉湖北省武汉市新洲一中 吴正文

一、引例

（1）椭圆的离心率e=______；

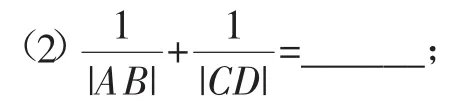
（3）若AB与CD的中点分别记为M，N，则直线MN恒过定点______.

二、简析

本题计算量较大，利用弦长公式求出|AB|与|CD|的表达式再结合单调性（或均值不等式）可以求出|AB|+|CD|的最小值为，故（1）与（2）得以解决，对于（3），则需求出直线MN的方程，进而发现它过的定点坐标，整个过程中注意到b2=1的特殊性，从而考虑到它的一般性是否成立.

三、探究

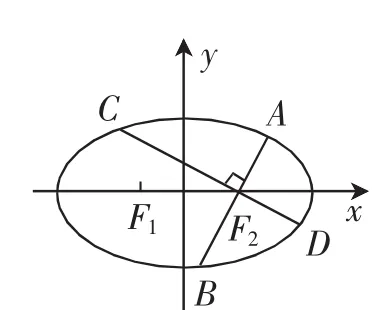
图1

到这里，引例中的3个问题都得到了解决.而且我们也能得到下面的结论：

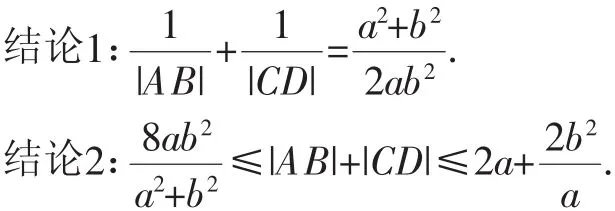
结论3：若AB与CD的中点分别记为M，N，则直线MN恒过定点

四、推广

在抛物线y2=2px中，过焦点的两条垂直相交弦AB与CD，有如下结论：

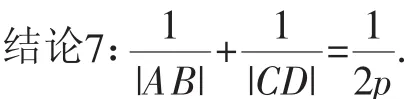
结论8：|AB|+|CD|≥8p.

结论9：若AB与CD的中点分别记为M，N，则直线MN恒过定点

五、结语

限于篇幅，上述对双曲线与抛物线的证明过程都没有给出来，感兴趣的读者可以验证一下.至此，我们感叹于圆锥曲线内部的和谐与统一，同时也激起我们对未知领域的向往.我们相信如果能够把这样的一种追求与探索的情感融入到平时的教学中去，感染学生，使之成为他们学习与成长中的一道风景，帮助学生领悟数学的魅力所在.