高三数学复习教学例题的选择与设计策略
陈丽洪
(福清第三中学,福建 福清 350 30 0)
在高三第一轮数学复习教学中,教师要帮助学生逐一复习每一章节知识点,并详细总结每一类题型解题的方法与步骤,为学生补缺补漏,很多后进生能够在有效的高三一轮复习后迎头赶上,重拾学习信心。因此,高三一轮有效复习显得尤其重要,而这一目标的完成主要在课堂教学中体现。例题是教师用作示范的典型数学问题,既能帮助学生回忆相关知识点,又起到训练学生数学思维和提高解题能力的作用。高三复习课主要以各类例题为载体,贯穿于整个课堂教学中。高三复习课堂教学的核心任务就是根据课堂教学目标,精心选择并设计出一两个或若干个例题,让数学课堂教学成为分析问题和解决问题的阵地,引导学生在解题的过程中完成复习任务。然而,数学教学中经常会有这样的现象:教师已经讲过的题,隔一段时间再做,学生的出错率还是很高。这种现象的出现,有学生的个人原因,但不应把责任都归咎于学生,教师也要进行反思:课堂例题的选择是否科学,课堂例题的设计能否符合学生的认知规律。因此,如何做好课堂例题的选择与设计是教师值得深思研究的一个问题。
一、针对复习教学内容的重难点与高考要求选择适当的例题
俗话说:“巧妇难为无米之炊。”教师提供给学生的是“米”还是“沙子”,是学生能否做好“这顿解题盛宴”的先决条件。数学例题的选择应为学生的思维活动,能够提供一个好的切入口,要为学生的学习活动找到一个好的载体,从而调动起学生的主观能动性。一个好的数学问题(例题)要具备以下几个特点:(1)具有包容性,能涵盖所复习知识的重难点,使所教内容重点得到强调,难点得以化解;(2)具有代表性,能代表某一类题型,使学生能举一反三,触类旁通,特别应能符合高考的要求,使学生知己知彼,决胜高考;(3)具有探索性,能调动学生能动性,独立判断,富有创造性;(4)能推广扩充到各种情形。在具体选择例题时,要能够选择符合学生能力的位于“最近发展区”的问题,因此教师要能细致地研究高考题、细致地研究学生思维发展以及知识水平,在此基础上,提出既能够有一定难度又能够使学生力所能及的问题。
在高中数学中,数列是数学教学的重要内容,也是高考考查的知识点之一,但考查难度一般不大。一般而言,学生通过有效的例题训练,就能较好地掌握。以《数列求和方法之裂项相消法》教学为例,在教学中,教师可以围绕重难点,先选择几个针对性较强的小问题,通过练习,将一个大问题中的难点化解,再选择几个符合高考要求的典型例题,分析题型特点,最后总结解决这一类问题的方法与步骤,引导学生发现解题规律。这类例题的训练对学生考试增分有显著效果。
(小问题环节)常见的裂项有:

选择意图:裂项是裂项相消法中的重难点,师生共同探讨这几个小问题,发现存在的问题,并总结规律。
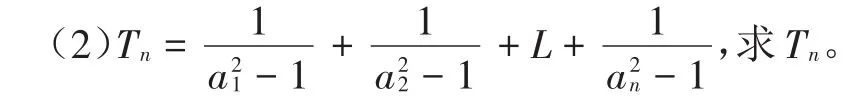
选择意图:第(1)题主要让学生经历裂项相消法的完整步骤,强调裂项时系数的配凑,考察学生的计算处理能力;第(2)题的题目形式有所变化,考察学生的应变能力,并再次总结解题步骤。
(1)求{a}的通项公式;(2)求数列的n前n项和;(3)求数列的前n项和。
选择意图:第(2)题再次让学生巩固裂项相消法的解题步骤;第(3)题是第(2)题的变式,让学生体会用裂项相消法解题时,也应特别注意消项后余项是哪些。
二、针对学生的解题能力与理解水平对例题进行递进式设计
选择好适当的例题,还要能够对例题的顺序和层次进行科学设计。若不能进行科学设计,只是胡乱堆砌,那只能使复习停留在初级程度,学生也只会是简单机械地模仿解题过程,甚至“消化不良”。经过数年的学习,高三学生对事物发展的认知已经达到了一个新的层次,他们的思维也具有更高的抽象概括性,根据高三学生的认知水平和高三复习内容的特点,可对所选例题进行递进式设计。这种设计模式有利于学生摸清知识的生成过程,引导学生主动探索,使学生遇到难题不丧失学习的主动性,以满足他们更强的探索和创新的需求。
(一)递进式设计例题,化解疑难题型
应用导数研究函数性质是高考考查的重点和难点,压轴题往往以导数应用为载体,因此,这一部分是高三复习的重要内容,其中,对含参数函数单调性的研究更是高三学子很难跨越的一道难关。
以《用导数研究含参函数的单调性》教学为例,在教学中,以一个基本问题为核心,针对某一类重要题型的复习,不断采用变式,形成从简到繁的解题过程,符合学生掌握知识的思维过程。复习过程层层递进,既具有挑战性,又能使学生感受到复习的成就感,提高学生学习兴趣。
例题设计展示:
题1.求函数f(x)=x3+3ax2-9a2x+12(a> 0)的单调区间。
设计意图:虽含有参数,但对参数进行限制,避免讨论,降低难度,但也起到引起注意的作用。讲解过程要强调此处对参数限制范围的重要性,为后续学习做铺垫。
设计意图:让学生巩固上一题的方法,学以致用,增强学生学习自信心,消除对含参数函数的恐惧心理。
题3.求函数f(x)=x3+3ax2+9x+12的单调区间。
设计意图:适当加大难度,激发学生求知欲。有了前两题做铺垫,学生能够自然过渡到对参数进行限制的思考,教师可引导学生弄清分类标准(二次方程判别式的讨论)。
设计意图:对参数进行限制,类似题1与题2,使学生有解题的意愿,但解题过程仍需对参数进行分类讨论(二次方程根的大小讨论),与题3相呼应,培养学生的解题应变能力。
题5.求函数f(x)=(a+1)1nx+ax2+1的单调区间。
设计意图:进一步巩固对含参函数单调性研究的方法,分类标准增加,有一定难度,教师适当引导,学生分组,自主讨论得到结论,体验成就感。
(二)递进式设计例题,把握知识本质
圆锥曲线也是高考考查重点,但大部分学生对圆锥曲线几何性质的理解并不深刻,为使学生能掌握圆锥曲线几何性质的本质,教学中也可采用递进式设计例题。以《椭圆》教学为例,在教学中,教师从问题出发,深挖问题内涵,抽丝剥茧,可以使复习教学逐层深入,让学生从较高的方位把握知识内容。具体例题设计如下:
(能力测评)例1.已知椭圆C的左焦点F1(-q1,0),且点在椭圆上,求C的标准方程。
设计意图:测评了解学生程度,更好把控课堂教学节奏,并回顾相关基本知识点。
设计意图:以高考题为例,引发学生兴趣,体会两个独立条件即可确定椭圆,并引出椭圆的几何性质。
设计意图:通过分析发现条件不足,不能确定椭圆大小,但能确定椭圆形状,从而体会椭圆离心率表示的几何性质。
(变式训练)例4.已知F1、F2是椭圆的两个焦点,P为椭圆上一点,∠F1PF2+60°,求椭圆离心率的取值范围。
设计意图:弱化条件,引出焦点三角形,体会焦点三角形能全面确定圆锥曲线,提炼出以直线研究曲线的方法,使复习达到另一高度。
高三一轮复习有知识点全面、题型多样等特点,所以复习方法也应多样化,以针对不同的复习内容和不同学生的实际情况。教师在例题的选择与设计上应精心思考,选择好的例题并对其顺序和层次进行合理设计,以提高学生学习效率,使复习达到事半功倍的效果。
总之,课堂例题的选择与设计中,教师应对每一道例题的设计意图都能做到心中有数,准确把握例题的分量,恰当确定它的使用方式,促进学生进行数学思考,帮助学生在解题过程中整体把握各章节知识内容,构建完整的知识体系,培养学生提高解题能力,掌握解决数学问题的策略与方法。此外,高三复习例题在选择与设计中还应贯彻解惑原则,也就是针对学生的学习误区设计例题;普化原则,即能从例题中提炼数学通性通法等。
当然,无论怎样选择与设计课堂例题,高三复习课不仅要体现宽度、厚度、高度,教师上课时还应该要有“温度”,即加强与学生互动,带动学生回忆知识点;授之以渔,帮助学生掌握解题模式和方法;并催发学生学习动力,增强学生战胜困难的意志和毅力,提高育人效果。

