基于连锁过载故障发生机理的关键线路辨识

何培颖，房鑫炎

（上海交通大学电子信息与电气工程学院，上海 200240）

电网的大规模互联在提高电网建设的经济性与输电效率的同时，也存在大停电事故的可能性[1-3]。大停电事故的研究表明[4]，运行在接近极限边缘的电力网络，因若干低概率事故（如检修期间发生局部故障等），引发潮流大范围转移，造成相邻元件过载，形成连锁过载跳闸而导致系统大面积停电。如何辨识在连锁故障中起到推波助澜作用的关键线路，并加以重点监控，对提高电力系统安全稳定性、降低大面积停电事故发生概率具有重要意义[5-6]。

文献[7]在系统网络结构和实时运行状态的基础上，构建包含电压偏移量、潮流系数、电气介数的指标体系辨识系统关键线路。文献[8-10]基于复杂网络理论，依据输电线路的介数指标来衡量线路的关键性，该方法默认系统功率沿着最短路径传播，与实际情况不符。文献[11]针对上述不足，利用直流潮流功率传输分布因子改进线路介数，并且考虑线路的运行状态，提出线路的综合关键性指标。文献[12]基于潮流熵，提出系统关键线路的评估模型，该方法认为潮流熵越大，线路负载率分布越不均衡，线路存在过载的可能性越大。文献[13]基于效用风险熵辨识关键线路，综合考虑了支路潮流转移特性和分布特性对连锁故障的影响，但该指标基于潮流转移量，需要进行大量的潮流计算，对于大电网系统其计算效率低下。

本文基于连锁过载故障的发生机理，从潮流转移特性出发，推导了连锁过载保护动作的判据公式，基于该判据公式建立了潮流转移指标与电网潮流熵，综合这两个指标定义了线路关键指标进行关键线路辨识，并提出两种连锁攻击模式，通过网络效能的降低验证所提关键指标的合理性。

1 潮流转移特性分析

电力系统某条支路因故障跳开后，假定各发电机出力和电网负荷没有改变，即每个节点的功率不变，那么这条支路原先承担的输送功率，将转移到其他支路，引起系统潮流的重新分布。

以图1为例说明支路断开后的潮流转移过程。假设支路7-8因故障断开，在不计电网中电力电子等非线性元件时，由线性网络叠加原理可知，断开支路7-8后的系统潮流分布由断开前潮流和等值电流源作用下的转移潮流叠加而成，如图2所示。

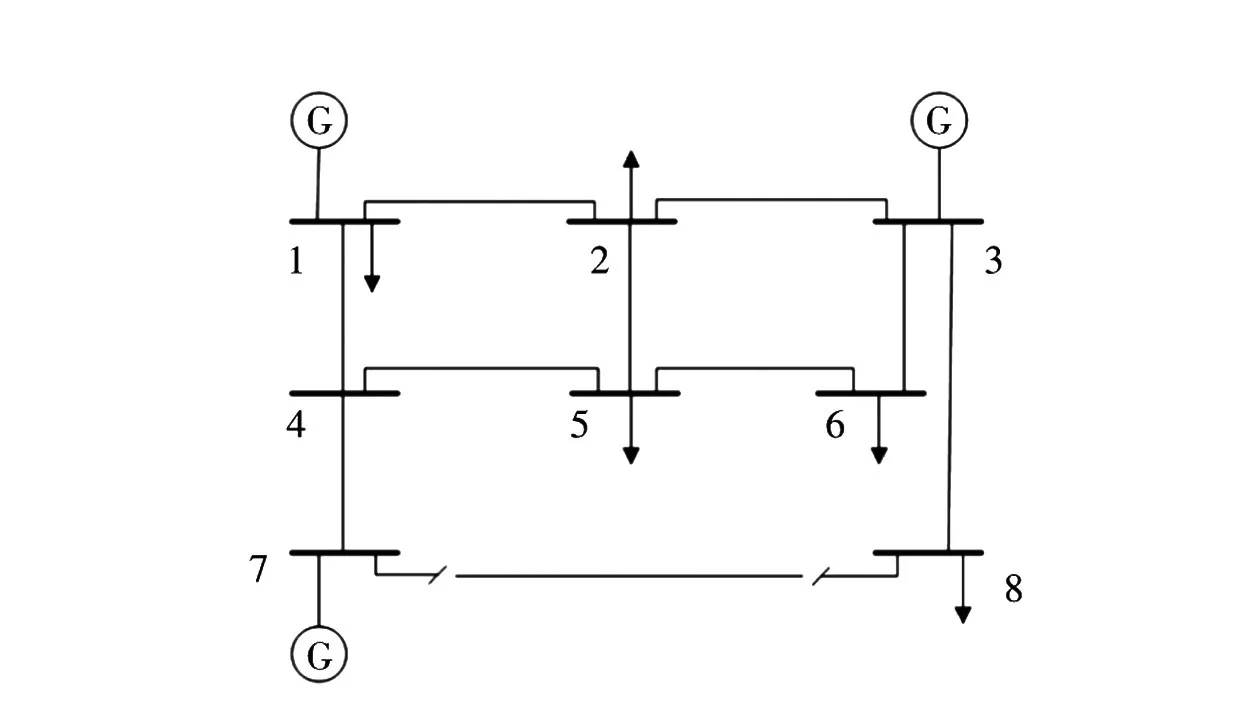
图1 8节点系统Fig.1 Eight-node system

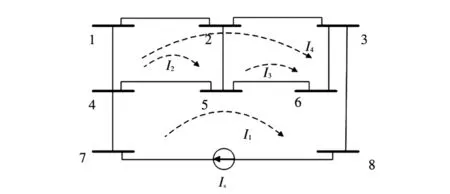
图2 潮流转移示意Fig.2 Diagram of flow transterring

由电路原理可知，单一电流源网络中，在网络参数确定条件下，各支路电流大小与电流源大小呈固定比例，即满足

式中：Is为电流源大小，与断开支路7-8前的原始电流大小相等，方向相反；λk,s为支路7-8断开时支路k的潮流转移因子；ΔIk为支路k的电流变化量。

叠加上原始网络电流，则支路7-8断开后，其他支路的电流大小为

式中：Ik为支路k上的电流大小；Ik0为原始网络电流。

在保证计算精度前提下，电网安全快速分析中，潮流转移因子的简化计算公式为

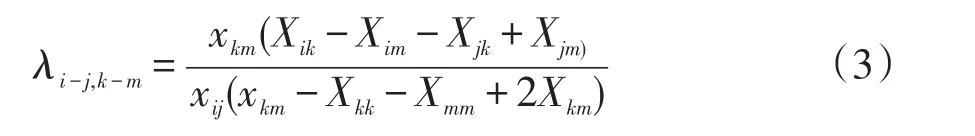
式中：Xij为阻抗矩阵中对应位置上电抗值；xkm为支路k-m的电抗值，xij为支路i-j的电抗值。

由于大电网系统中，节点电压可通过发电机励磁系统等电压调节装置而维持不变，因此式（2）中的电流公式也可写成功率计算公式，即

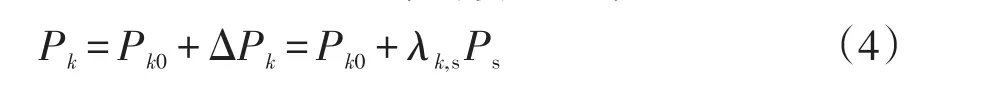
式中：Pk为支路k上的功率大小；Pk0为原始网络功率；Ps为电流源功率；ΔPk为支路k的有功功率变化量。

2 线路关键指标

2.1 连锁过载故障发生机理

引出线路关键指标之前，先对连锁过载故障的发生机理做一简单分析。假定支路k的过载保护继电器设定值为额定功率的γ倍。现有支路s因故障切除，切除前支路k处于额定功率Pk0状态，切除后其功率计算公式为

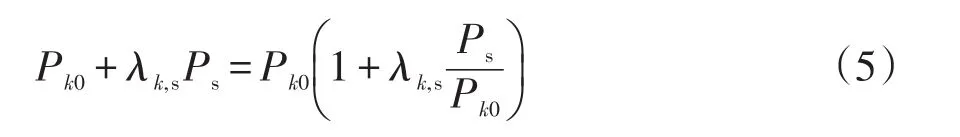
支路s切除后，引起支路k连锁过载保护动作的判据为

如果满足式（6）判据，那么支路k过载保护动作，支路k断开，其潮流进一步转移，从而导致更多线路发生连锁过载跳闸，最终引发电网的大面积停电故障。

2.2 功率转移指标

从式（6）可以看出，支路切除，引起其他支路过载的重要依据之一是λk,sPs/Pk0。基于此，定义支路功率转移指标为

式中：Wl为支路l的功率转移指标；Pl为支路l的有功功率；Pi为支路i的有功功率；λi，l为支路 i相对于支路l的潮流转移因子。

功率转移指标Wl值越大，说明该支路的断开，引起的潮流转移越严重，从而引发连锁过载故障的可能性也越大。因此该指标能够反映线路的断开对连锁过载故障影响的大小。

2.3 电网潮流熵

由式（6）可知，支路断开引发连锁过载的另一依据是γ的大小。γ反映了支路的抗越限能力。为便于计算，可用线路负载率来表征支路的抗越限能力，可表示为

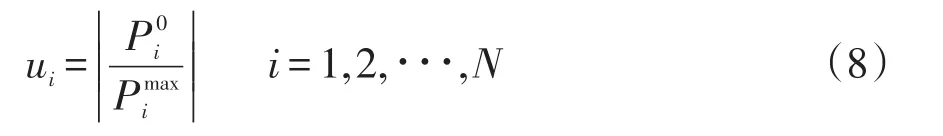
式中：ui为支路i的负载率；为系统当前运行状态下支路i的有功功率；为支路i允许的最大有功功率。

支路断开引发潮流转移，使得负载率分布的均衡性降低。为定量评价负载率分布均衡性，引入熵的概念。熵是系统混乱和无序状态的度量指标，潮流熵可以反映系统潮流分布的不均衡性，借助该指标可评估负载率分布均衡性对电网连锁故障的影响。

给定常数序列U={U1，U2，…，Uk，…，Un}（本文中取 U={0，0.02，…，1.6}）。用 lk表示负载率 ui∈（Uk，Uk+1]的线路条数，对不同负载率区间内的线路条数概率化，可表示为

式中，F（k）为负载率ui∈（Uk，Uk+1]的线路条数占总线路数N的比例。

定义支路潮流熵为

式中：Hl为支路l潮流熵；C为常数，本文取ln10。

由式（10）可知，当断开支路l时，若其潮流熵很大，则表明负载率分布很不均衡，有的线路负载率很高，其抗越限能力很弱。因此支路潮流熵能够表征γ值，运用该指标来反映支路断开对连锁故障过载的影响是合理的。

2.4 关键指标

综上，综合功率转移指标和潮流熵，可定义线路关键指标为

式中：Vl为支路l关键指标；wl和hl分别为归一化后支路l的潮流转移指标与潮流熵；Wl可由式（7）计算得到；Hl为断开支路l后按式（10）计算得到。

3 综合关键指标与拓扑关键性的关系

3.1 网络效能

为验证由式（11）线路关键指标辨识得到的关键线路的合理性，引入网络效能的概念。

大量研究表明，电网具有小世界特性，即电网中存在少量远程连接，这些远程连接的存在使得电力网络中负荷节点与发电机节点之间保持较小的电气距离和较高的网络效能。断开远程连接，会极大地降低系统的输电能力和网络效能，导致电网的功率失衡，从而引起电力系统的失稳。因此可通过网络效能的下降程度来验证线路关键指标的合理性。

网络效能的定义[14]为

式中：J为网络的效能；i，j为网络G中的节点编号；N为网络节点总数；dij为以支路电抗为权重的节点i、j间的最短距离。

3.2 故障模式

为了探索所提关键指标在故障传播中的作用，本文按以下两种模式对系统进行攻击。

1）高关键指标攻击模式

采取连锁攻击关键指标最大的线路，即每次选择一定量关键指标最高线路断开，计算剩余系统各线路的关键指标和系统的网络效能，然后再攻击剩余系统中关键指标最高的线路，以此类推。

2）随机连锁攻击模式

采取随机选取线路攻击方式，即每次随机选择一条线路断开后，重新计算系统网络效能，然后再随机选择一条线路断开，以此类推。

若高关键指标攻击模式下系统的网络效能相比随机连锁攻击模式下降明显，则表明在电力网络中，关键指标高的线路就是那些对小世界特性有重要影响的远程连接，可以使用关键线路指标作为电力网络关键线路的辨识指标；否则说明关键线路指标在辨识关键线路上是无效的。

4 算例仿真

以IEEE-39节点系统为例，仿真验证本文所提线路关键指标的有效性和可行性。IEEE-39节点系统包括10个发电机节点，19个负荷节点，46条支路，其拓扑结构如图3所示。

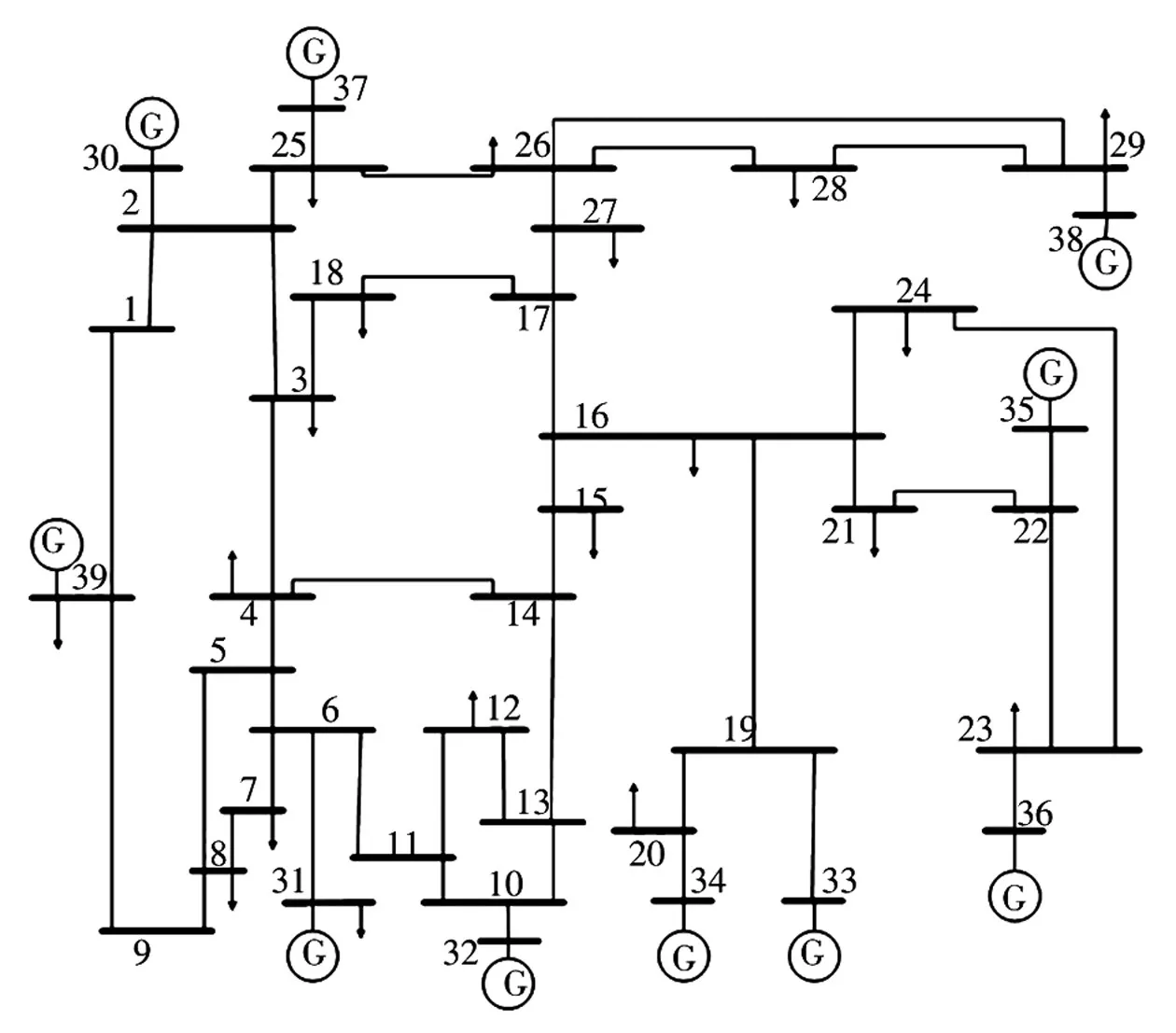
图3 IEEE-39节点系统Fig.3 IEEE 39-node system

4.1 关键线路辨识

计算IEEE-39节点系统中每条支路的关键指标并进行排序，得到排名前10的支路为20-34、29-38、22-35、25-37、6-31、10-32、16-19、19-33、2-30、23-36。

在排名前10支路中除支路16-19外，其余支路均为发电机功率送出支路，断开这些支路将导致发电机功率无法外送，影响系统功率平衡，因而这些支路关键性排名靠前是合理的。

在实际电网中，系统调度、检修人员一般都认为发电机功率送出支路具有较高的重要性而加以重点监控，因此在搜索关键支路时，可以默认这些线路关键性很高，不需要把这些支路列入搜索范围。

以IEEE-39节点系统为例，剔除发电机功率送出支路2-30、6-31、10-32、19-33、20-34、22-35、23-36、25-37、29-38，重新计算各条支路的综合关键指标，并将结果与文献[13]运用效用风险熵指标所辨识关键线路结果对比，如表1所示。

从对比结果看出，两种方法所辨识前10支路中有6条相同支路，可以认为两种方法的辨识结果大体相同。但是文献[13]方法基于潮流转移量，需要进行大量反复的潮流计算，对于大电网系统其计算效率低下，而本文方法只需输入电网参数获取潮流转移因子，再运行一次潮流计算即可，计算效率很高，特别对于大电网系统其优势更加明显。

下面对所搜索前十关键线路对电网的重要性进行说明：支路16-19为33、34两个发电机节点的唯一功率送出支路，断开该支路将导致这两个发电机节点的功率无法外送，通过仿真发现，断开该支路后，将导致系统潮流无法收敛，因此该线路综合关键指标最高是合理的；支路13-14、2-25、4-5、2-3、19-20同样也是发电机功率外送的关键通道，断开这些支路，会导致部分区域功率失衡，从而引发系统功角失稳；支路15-16处于系统拓扑结构中的关键位置，对整个系统的功率输送起着重要作用；支路26-27、6-11、16-24承担着很大的输送功率，对其开断，将造成潮流的大范围转移，容易引发连锁过载故障，因此其重要性也很高，需要加以监控。由此看出，基于本文关键指标辨识的关键线路符合IEEE-39系统中的关键环节。

表1 关键线路辨识结果对比Tab.1 Comparison of identification results among critical lines

4.2 两种攻击模式下系统网络效能分析

采用第3.4节提出的两种攻击模式，记录下每次攻击的网络效能，如图4所示。横轴为攻击次数，纵轴为攻击后网络效能与原始网络效能的百分比，可表示为

式中：G（t）为攻击t次后网络效能与原始网络效能的百分比；J（t）为攻击t次后由式（12）计算得到的网络效能；J0为攻击前网络效能。

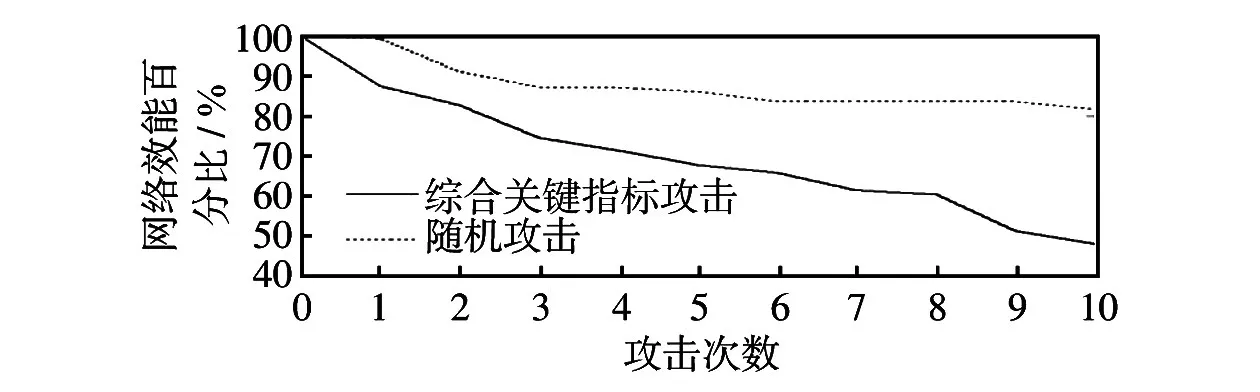
图4 两种攻击模式下网络效能变化Fig.4 Variation of network efficiency in two attack modes

从图4可以看出，IEEE-39节点系统在随机攻击模式下，其网络效能下降很少，经过10次攻击后，其网络效能仍然维持在80%以上；而在关键指标攻击模式下，其网络效能下降明显，经过10次攻击后，其网络效能已下降到50%以下。

通过上述分析可知，IEEE-39节点系统在随机连锁攻击下具有较好的鲁棒性，而关键指标连锁攻击表现极为脆弱，从而验证了本文提出的关键指标辨识关键线路的有效性。

5 结语

本文根据支路断开后的潮流转移特性，分析了连锁过载故障的分析机理，得出影响系统发生连锁过载故障的两个指标：潮流转移指标和电网潮流熵。综合这两个指标给出了线路关键指标的定义，对关键线路进行辨识，并提出两种连锁攻击模式，根据网络效能的降低验证所提关键指标的合理性。最后通过IEEE-39节点系统为例进行仿真，验证了所提方法的合理性与有效性。