基于径向基函数神经网络的PI-准比例谐振控制策略

李圣清，张 茜

（湖南工业大学电气与信息工程学院，株洲 412007）

关键字：并网逆变器；电流控制；准比例谐振控制；神经网络

随着光伏、风力发电等新能源技术的发展，绿色分布式电源DG（distributed generation）并网技术的研究也越发深入。并网逆变器作为DG与公共电网连接的重要接口装置，其控制是实现电能高效利用的基础[1]。

传统的PID控制、重复控制、滞环控制等由于算法简单、易于实现，被广泛应用于并网逆变控制器中，但是在跟踪正弦参考信号时存在幅值和相位的稳态误差以及抗干扰能力差等缺点[2]。已有学者对并网控制器的优化设计做了大量的研究[3-7]。文献[8]提出在不平衡电网电压条件下，比例积分-降阶谐振PI-ROR（proportion integral-reduced order resonant）调节器可直接对输出电流无差控制，能改善并网逆变器的动态性能，提高系统在不平衡电压条件下的运行能力。文献[9]提出PI与准比例谐振QPR（quasi proportional resonant）联合控制的光伏并网电流优化策略，实现了电流的无静差跟踪，抑制直流分量。文献[10]在两极式单相并网发电系统控制策略中，在误差反向传播BP（back propagation）神经网络算法的基础上加入了功率跟踪环节提高了系统动态性能，改善了功率突变时逆变器的电流波形，提高了系统的运行效率。文献[11]为了实现神经网络模型在实际仿真中的应用，提出了一种神经网络模型接入电力系统分析综合程序PSASP（pow⁃er system analysis software package）的改进方案，使局部回归网络Elman神经网络模型能适应于各种DG统一建模的需要。文献[12-13]针对单相并网逆变系统高度非线性的特性，提出了一种基于神经网络参数自整定的QPR控制方法，解决了传统逆变器控制系统自适应能力差的问题。

本文基于传统的PI控制器和QPR控制器，提出了一种采用基于径向基函数RBF（radial basis function）神经网络参数自整定的PI-QPR复合控制策略，提高了光伏并网系统的抗干扰能力，降低了电流的总谐波畸变率THD（total harmonic distor⁃tion）。仿真结果证明了该策略的有效性。

1 三相并网逆变器数学模型

图1为并网逆变器主电路拓扑结构图，Udc为直流侧电压；ua、ub、uc分别为相电压；C为直流侧电容；ia、ib、ic分别为逆变器输出电流；ea、eb、ec为电网电压；L为交流侧电感；R为交流侧电阻[14]。

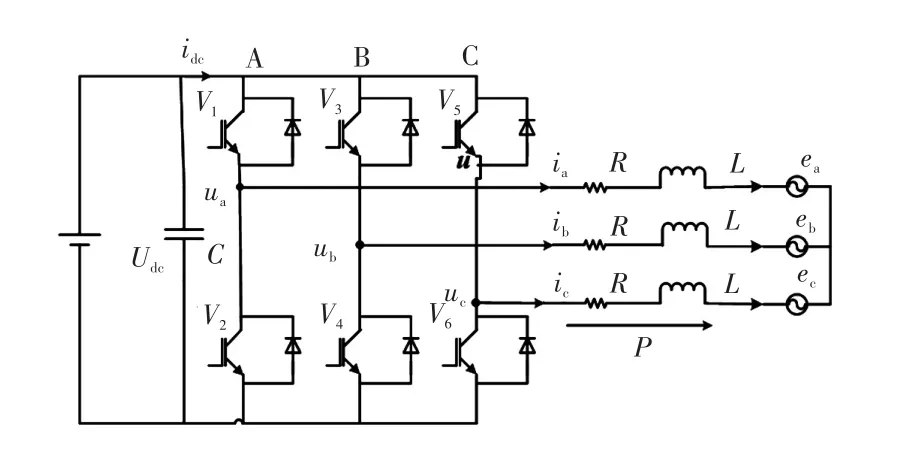
图1 并网逆变器主电路拓扑结构Fig.1 Topology of the main circuit in grid-connected inverter

三相电网平衡时，由基尔霍夫电压定律得

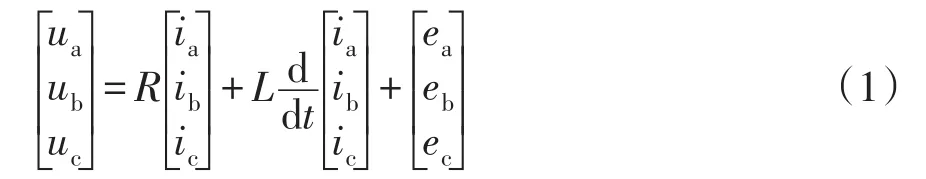
Clark变换为

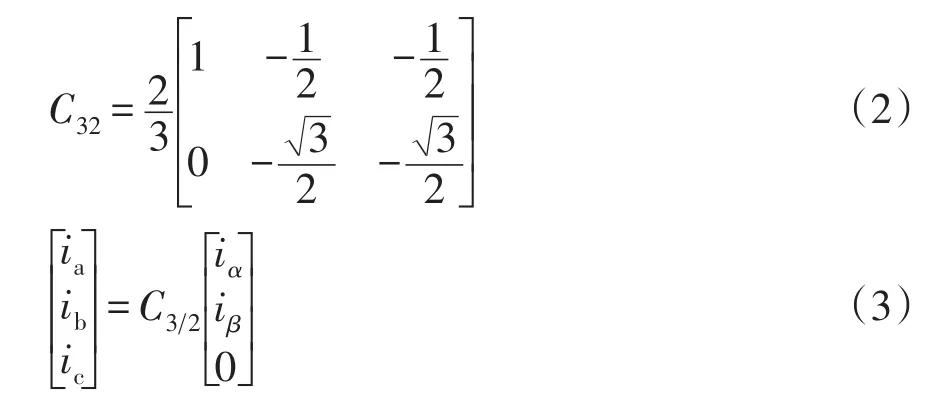
式（3）经过Clark变换可得

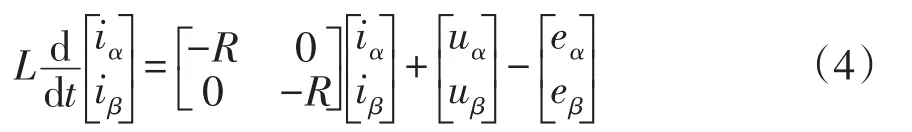
式中：uα、uβ分别为两相静止坐标系下的电压分量；eα、eβ分别为两相静止坐标系下的电网电压分量；iα、iβ分别为两相静止坐标系下的电流分量。

由式（4）可得在αβ坐标系中不存在耦合现象，可以看作两个独立的单相逆变器处理。

2 PI-QPR复合控制器

传统PI控制器具有改善系统幅频特性和稳态性能的优点，其传递函数GPI(s)为

式中，Kp1、Ki1分别为PI控制器的比例参数和积分参数。

根据式（5）可得PI控制器的波特图如图2（a）所示，基波频率（50 Hz）前幅值增益较大，到达基波频率及以上时，幅值频率保持不变，其频率控制范围有限，系统存在稳态误差

为了改善传统PI控制器存在的稳态误差，实现逆变器输出电流的无静差跟踪，本文提出一种PIQPR复合控制方法，其中QPR控制属于内模控制，其传递函数Gpr(s)为

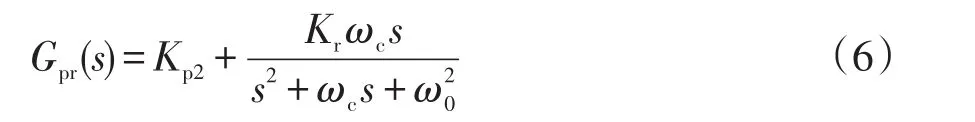
式中：Kp2、Kr分别为QPR控制器的比例参数和谐振参数；ωc为频带宽度；ω0为谐振基波角频率。

根据式（6）可得QPR控制器波特图如图2（b）所示，在基波频率处QPR控制器的增益较小，控制频率范围较大，减少了电网频率波动带来的影响，具有很好的稳定裕度，能实现电流的无静差跟踪。

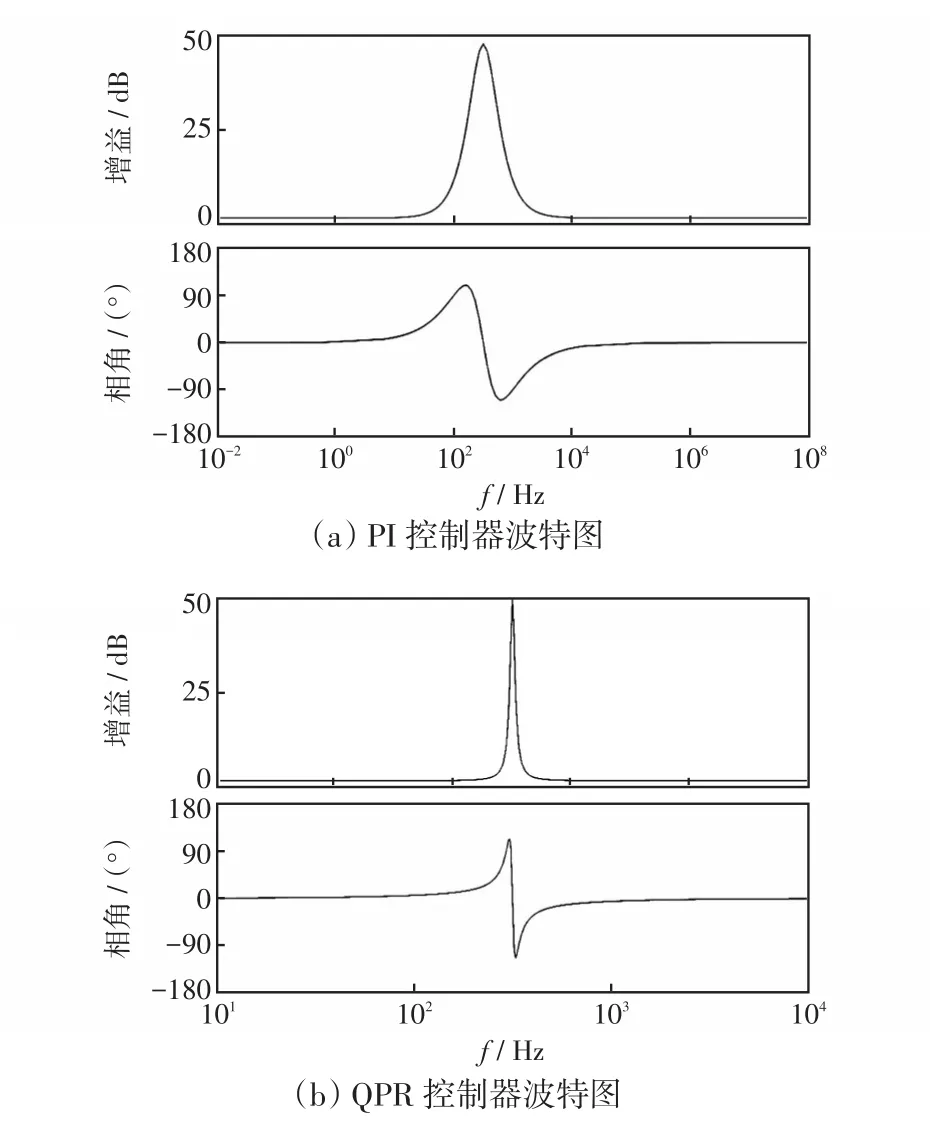
图2 PI与QPR控制器的频率特性比较Fig.2 Comparison of frequency response between PI and QPR controllers

为了易于实现QPR的数字控制，将式（6）中的谐振部分分解为3个简单积分y(s)、m(s)、n(s)，可表示为

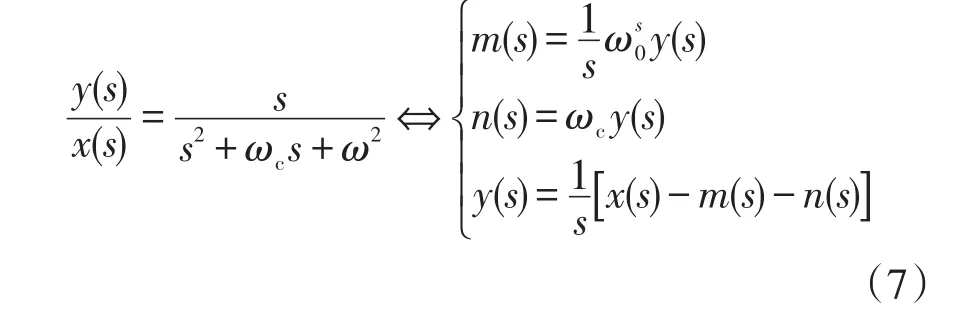
将模拟信号数字离散化，可得第k次采样时刻控制器的输出为

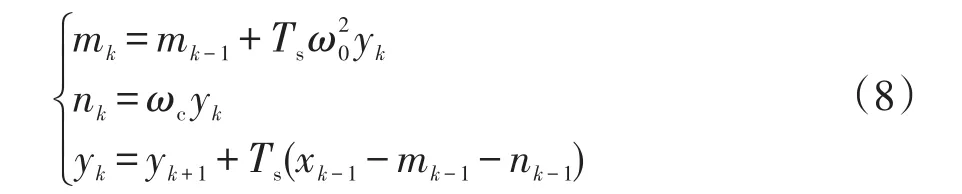
式中,Ts为采样周期。

最后可得PI-QPR算法控制框图如图3所示。

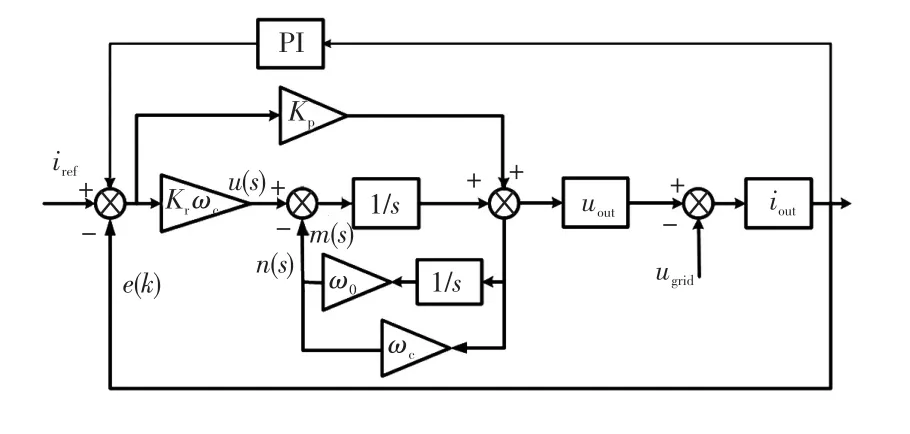
图3 PI-QPR算法控制框图Fig.3 Block diagram of PI-QPR algorithm control

3 基于神经网络PI-QPR复合控制策略

3.1 RBF神经网络

RBF神经网络具有学习速度快、非线性逼近能力强等优点，因此在自适应控制技术中得到了广泛的应用。该神经网络是一种具有单隐层的3层前馈网络，能以任意精度逼近任意连续函数。RBF神经网络结构如图4所示[15]。

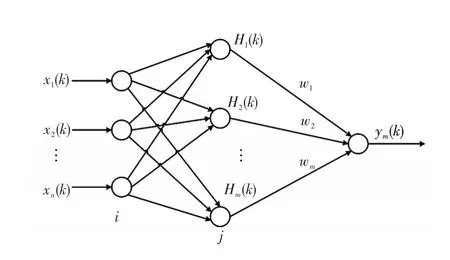
图4 RBF神经网络结构Fig.4 Structure of RBF neural network

设RBF为Hj(x)，j=1,2,…,m，神经网络的输入 为 X=[x1,x2,…,xn]，中 心 节 点 矢 量Cj=[cj1,cj2,…,cjn]，ρj为第j个基函数的基宽，Hj（x）表达式为

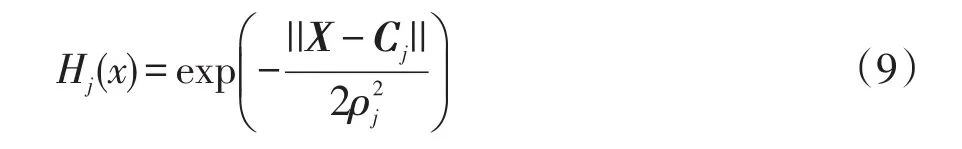
采用梯度下降法可以将RBF神经网络权值调整为

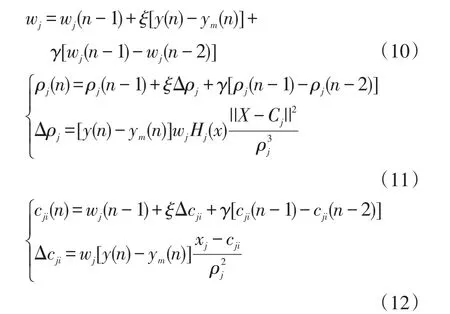
式中：ξ为学习速率；γ为动量因子；wj为第j个神经元的权值；wj(n)为采样点第n时刻第j个神经元的权值；y(n)为第n时刻系统的实际输出；ym(n)为第n时刻第m个神经元的输出；ρj(n)为第n时刻第j个径向基函数的基宽；Δρj为第j个径向基函数基宽的变化量；cji(n)为第i个和第j个神经元中心节点矢量。

3.2 改进型PI-QPR控制策略

如图5所示，本文将基于RBF神经网络的改进型PI-QPR复合控制下的电流控制分为PI-QPR复合控制和RBF神经网络参数整定两个部分。PIQPR控制器对逆变器进行电流内环控制，其中PI控制器主要用于提高系统响应速度，增强系统稳定性，QPR控制器用于消除系统稳态误差。RBF神经网络用于对QPR参数进行在线整定。RBF神经网络输入层的3个神经元分别为逆变器的输出电流iout、参考电流iref和电流误差ei；输出层的神经元分别对应QPR控制器参数Kp、Kr、ωc。RBF神经网络会根据系统的运行状态在线学习，通过自动调整各神经元之间的权值对QPR控制器的3个参数在线整定，以达到适用于当前状态的最优值，同时当系统出现波动时能够准确地跟踪并网电流，提高了系统的动态性能，进而提高逆变器的转换效率。

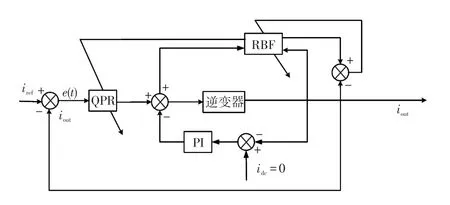
图5 基于RBF神经网络的PI-QPR复合控制下电流控制框图Fig.5 Block diagram of current control under PI-QPR compound control based on RBF neural network

RBF神经网络控制算法通过Matlab/Simulink仿真平台生成S-Funcation模块，通过PI-QPR控制器对逆变器的输出电流进行内环控制，电网电压同步信号通过锁相环PLL（phase locked loop）得出，如图6所示。

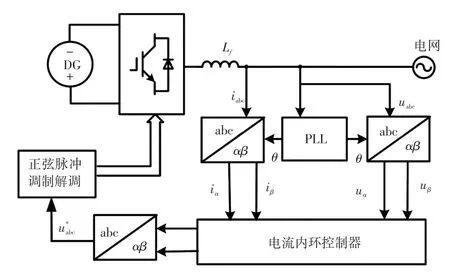
图6 三相并网逆变电流内环控制框图Fig.6 Block diagram of inner current loop control of three-phase grid-connected converter

4 仿真及结果分析

为了验证基于改进型PI-QPR控制器的并网逆变器控制策略的有效性，基于Matlab/Simulink平台建立了并网逆变器系统模型，其主要参数为直流侧电压600 V，直流侧电容5 000 μF，滤波电感2 mH；交流电网侧电感0.125 mH，交流侧电阻0.1 Ω，电网频率50 Hz，逆变器开关频率20 kHz；PI控制器参数Kp1=0.8，Ki1=0.4；QPR控制器初始参数 Kp2=1.5，Kr=50，ωc=10。

图7和8分别为PI控制与基于RBF神经网络的改进型PI-QPR复合控制的输出电流跟踪效果，id、分别为在两种控制策略下d轴分量的输出电流。由实验结果分析可知，前者直流量波动较大，与参考值偏差较大，而后者的电流跟踪效果更好，与给定值基本重合。图9和图10分别为两种控制方式下并网电流波形，后者更接近理想正弦波，ia、ib、ic分别为三相并网电流。图11和12分别为两种控制方式下的并网电流THD对比，A为谐波幅值相对于基波幅值的百分比，采用神经网络参数整定的PI-QPR复合控制输出电流总谐波畸变率比前者减少了1.01%，电流质量更高。

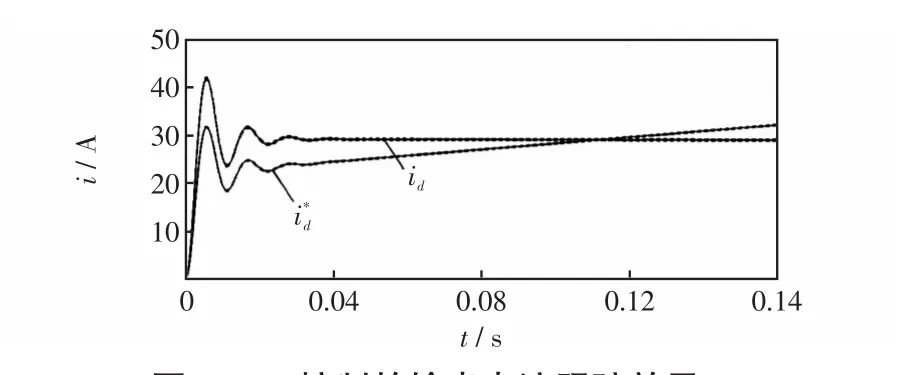
图7 PI控制的输出电流跟踪效果Fig.7 Effect of output current tracking under PI control

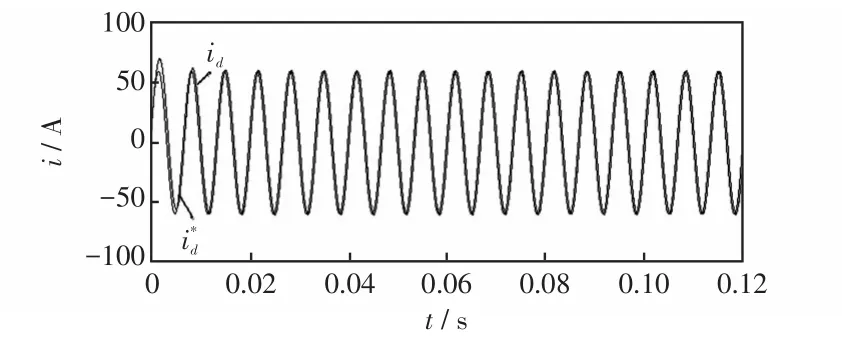
图8 基于RBF神经网络的PI-QPR复合控制下的输出电流跟踪效果Fig.8 Effect of output current tracking under PI-QPR compound control based on RBF neural network

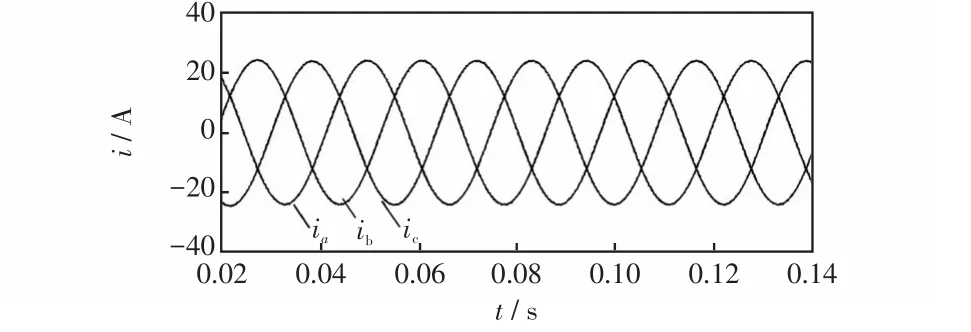
图9 PI控制下并网电流Fig.9 Grid current under PI control

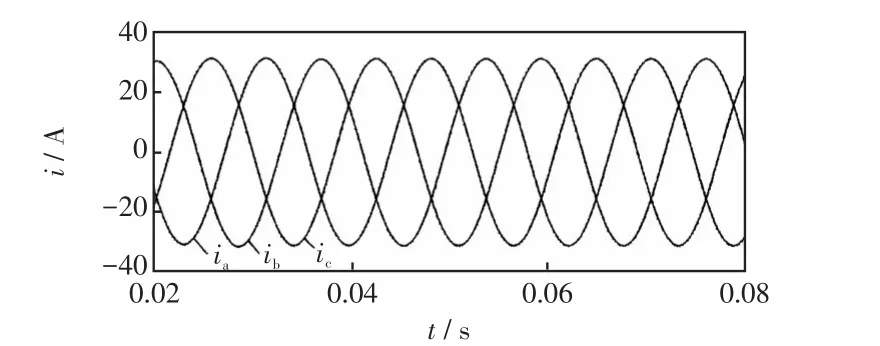
图10 基于RBF神经网络的PI-QPR复合控制下并网电流Fig.10 Grid current under PI-QPR compound control based on RBF neural network

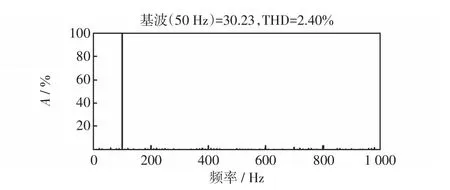
图11 PI控制下并网电流波形FFT分析Fig.11 FFT analysis of grid current waveform under PI control

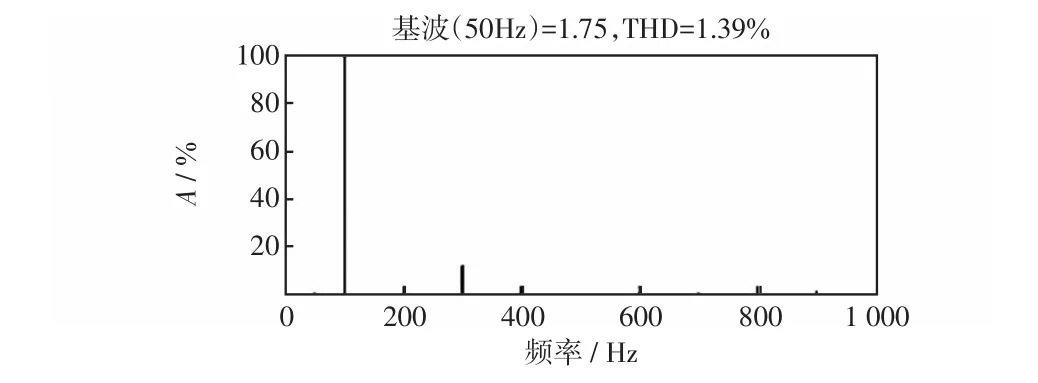
图12 基于神经网络的PI-QPR复合控制下并网电流波形FFT分析Fig.12 FFT analysis of grid current waveform under PI-QPR compound control based on neural network

5 结语

本文提出了一种适用于三相并网逆变器的基于RBF神经网络的改进型PI-QPR复合控制策略，目的在于改善传统PI控制器存在稳态误差以及QPR控制器参数难整定等问题。该控制策略能实现电流的无静差跟踪，减少电流畸变率，并通过RBF神经网络的在线自适应参数整定能力。当电流信号发生波动时能迅速跟踪，在线得出PI-QPR复合控制器的最优参数，并网逆变器采用此种复合控制策略得到的电能质量更高，同时提高了系统的自适应力和抗干扰能力。最后，对本文提出的策略进行仿真，同时与PI控制下进行分析比较，实验证明了该策略的正确性与优越性。