复杂地质条件下砂岩渗透机理及模型探讨

吴志刚 罗有权 张黎红 陈行

摘要：为分析研究砂岩渗透性受各项地质因素影响的相互关系，对不同泥质含量和孔隙率的砂岩进行了不同应力环境下的三轴渗透试验。试验结果表明：渗透率随着应力加载全过程呈先减小后增大的趋势；体积变形扩容点与渗透率的突变点相对应，能准确反映渗透性的变化态势；偏应力、泥质含量及孔隙率一定时，渗透率随围压的增大呈负指数型减小；同等应力环境下，渗透率随孔隙率与泥质含量比值的增大呈指数型增加。通过分析探讨，建立了渗透性与围压、孔隙率、泥质含量相关的渗透经验模型以及随体积应变变化的扩展经验模型，该模型能够较为准确地反映复杂地质环境下砂岩渗透性的变化趋势。

关键词：砂岩；三轴；渗透；体变；孔隙率；泥质含量；模型

中图分类号：TU45 文献标志码：A doi：10.3969/j.issn.1000-1379.2018.05.023

随着现代水电、交通、矿山、油气探井工程建设的蓬勃发展，其地下围岩力学性质受到越来越多的关注和研究，其中砂岩是这些工程中最为常见的岩石之一，其渗透特性对工程的安全和稳定具有重要影响，一直是有关专家学者研究关注的焦点[1-2]。

姜振泉等[3]对砂岩、页岩、黏土岩等软、硬岩进行了不同压力条件下的全应力一应变过程渗透对比试验，认为岩石变形破坏过程中的渗透性主要取决于变形破坏的形式和特点；张守良等[4-5]研究了砂岩、泥岩等变形破坏过程中渗透率随荷载的变化规律，并对其影响因素进行了探讨，同时建立了渗透率与应力之间的关系式；张渊等[6]分析探讨了温度和孔隙压力对细砂岩渗透率的影响规律，认为渗透率同时存在门槛值温度和孔隙压力门槛值；俞缙等[7]分析了全应力一应变过程中砂岩渗透率随其脆性、延性变化的特点及渗透率一轴向应变和渗透率一体积应变之间的关联性；王小江等[8]利用三轴耦合试验机进行粗粒砂岩不同围压条件下变形破坏过程的渗流试验，分析了粗粒砂岩变形破坏过程中渗透性变化规律和围压对于粗粒砂岩渗透性质的影响，推导了渗透系数与体积应变的关系。

砂岩的渗透性不仅受应力环境、粒度、温度、孔隙压力等因素的影响，而且与自身的物质成分含量相关，大量的试验研究表明，泥质含量的多少也直接影响着砂岩的渗透性。在测井钻探技术研究中，一些学者已对泥质含量对砂岩孔隙率、渗透率等的影响进行了相关研究。王连国等[9]应用突变学理论，研究了试验全过程中渗透率与应力、应变之间的关系，建立了岩石渗透率与应力、应变关系的尖点突变模型。

上述研究大多仅针对砂岩渗透率与某一特定的影响因素，而关于复杂地质环境下的砂岩渗透率研究较少，如何预测复杂地质环境下砂岩渗透性的变化规律显得尤为重要。因此，笔者尝试利用不同泥质含量及孔隙率砂岩进行三轴全应力一应变渗透试验，并根据试验结果，得到复杂地质环境下砂岩的综合渗透经验模型。

1 试验概况

1.1 试验试件

试件取自某水电厂房地下工程埋深100～120m处，以中等粒径颗粒为主，属灰黑色沉积纹理中砂岩，通过D/Max-3B型X射线衍射仪分析得知砂岩的主要成分为石英、长石、方解石、泥质胶结物等，根据泥质胶结物含量将其分为4组，其平均泥质含量ω分别为4%、15%、24%、31%，通过试验测定的对应孔隙率φ分别为17.8%、11.2%、7.8%、3.7%。将现场取回的岩芯按《工程岩体试验方法标准》（GB/T 50266-2013）[10]通过钻、切、磨的方法加工成50mm（直径）×100mm（高）的标准圆柱体试件。

1.2 试验方案

试验共设σz=5、10、15、20MPa四个围压，施加围压后，对砂岩进行一次初始渗透测试，之后在应力加载过程中，用等加载应力差的测试方式，在峰前每隔10MPa进行一次测试，峰值应力处进行一次渗透测试，在峰后视情况进行2～3次测试。每次渗透测试时上下两端初始压差均为1MPa，围压加载速率为3MPa/min，荷载加载速率为60kN/min。

2 试验结果及分析

2.1 应力一应变分析

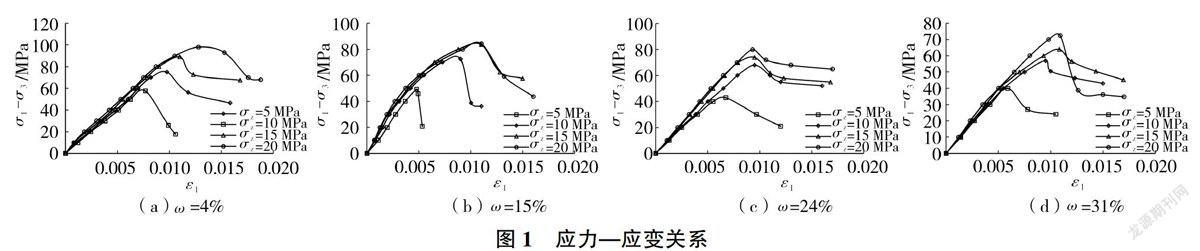
渗透试验各组砂岩的应力一应变关系见图1（σ1为第一主应力，σ3为第三主应力，σ1-σ3为偏应力，ε1为轴向应变）。從应力一应变曲线可以看出，砂岩在三维应力状态下的变形过程包括压密阶段、弹性变形阶段、塑性变形阶段及峰后残余阶段。相同泥质含量下，随着围压的升高，砂岩的变形能力逐渐增强，塑性变形特征更明显，破坏时达到的轴向应变有逐渐增大的趋势，而破坏方式逐渐由脆一延性向延性破坏转变，并呈典型的剪切破坏特征。

2.2 渗透率一应变分析

为进一步分析砂岩渗透率与应变之间的关系，点绘了5MPa围压对应的各泥质含量下渗透率随轴向应变及体积应变的演变曲线，见图2（εv为体积应变、к为渗透率）。从图2可以看出，渗透率随轴向应变的增大，先略微减小并逐渐趋于动态平衡状态，这一阶段主要对应砂岩的压密及弹性变形区，对应的体积应变逐渐增大，砂岩处于体积压缩阶段，该阶段主要为岩石封闭应力调整。试件各项力学性质有所增强，即压缩硬化过程，此时渗流通道主要为砂岩的原始微裂隙、微裂纹，而由于砂岩初期的压密闭合作用使得渗透率相对于加载前略有减小，在弹性阶段并没有产生新的损伤，因此渗透率维持在某一相对恒定值；砂岩进入屈服阶段后，渗透率逐渐增大，并在峰前快速增大，在此阶段，新生裂纹逐渐产生并发展，水通过这些新生裂纹进行渗流，大量裂纹贯通，形成宏观裂纹和裂隙，此时砂岩处于体积剪胀损伤状态，因此渗透性会显著增强；峰后残余变形阶段，渗透系数相对峰值附近有所减小，此阶段砂岩处于软化剪胀损伤状态，岩石内部应力重新分布，产生的破裂面在荷载作用下又被重新压密，且破坏时产生的碎屑和泥质颗粒会堵塞部分通道，同时由于峰后阶段采取应变控制的方式，使得轴向应力出现松弛现象，裂纹扩展速度变缓，因此渗透率均出现一定降低。由上述分析可以看出，体积应变的发展演化过程反映了试件内部的硬软化一损伤过程，体积变形扩容点与渗透率的突变点相对应，能准确反映渗透性的变化。

2.3 渗透率一围压分析

相同泥质含量及孔隙率下（以泥质含量4%为例），砂岩的渗透率随围压的变化情况见图3。由图3可知，相同泥质含量及孔隙率的砂岩在同一加载偏应力下，围压越大，渗透率越小，随着围压的升高，渗透率呈对数函数减小，表明渗透性因更大的侧向约束力使得砂岩试件内部结构更加致密而逐渐减小。砂岩的初始渗透通道主要依靠原始微裂隙和微孔隙，但围压越大会使得内部颗粒更大程度上被挤压密实，因此渗透率越小；应力加载过程中，由于存在更大侧向约束力，使得试件内部的渗流通道发展更为缓慢，因此渗透率随围压的增大而减小。

2.4 渗透率—泥质含量（孔隙率）分析

同等应力环境下，砂岩的渗透率随泥质含量及孔隙率的变化情况见图4（仅列出围压5MPa、偏应力0MPa以及围压15MPa、偏应力10MPa的情况进行说明）。可以看出，随着泥质含量和孔隙率的增大，渗透率分别呈线性减小和增大，原因是泥质胶结物颗粒较细，与其他物质相互胶结形成的渗透通道更细小，泥质胶结物对渗流通道的阻塞作用越明显，而砂岩内部颗粒间排列越紧密使得孔隙率越小，砂岩渗透率越小。

王小江等[8]在油气测井技术研究中通过大量理论分析认为：处于同一层面（即所处应力环境基本一致）的砂岩，其渗透率随孔隙率与泥质含量比值的增大呈幂函数递增。借签该研究经验，可以得到本次试验砂岩随孔隙率与泥质含量比值的关系（以初始渗透率为例），见图5。从图5可以看到，本次试验砂岩在同一围压下的初始渗透率K0与φ/ω之间成良好的对数函数关系（复相关系数均大于0.97），即式中：c、d为与围压相关的经验常数。

3 复杂地质条件下砂岩渗透经验模型

3.1 模型的建立与验证

一般而言，围岩应力的大小随地层深度的增大而增大，从上述试验研究结果可以看出，砂岩的渗透性不仅与孔隙率、泥质含量等相关，还与围压大小密切相关。因此，在前人研究的基础上，认为砂岩的渗透率是这三者的函数，即

K =f（σz，φ，ω）（2）

由式（1）可知，同一围压下к0与φ/ω成良好的对数函数关系，而通过统计分析发现各围压下经验系数c、d与围压存在图6所示的函数关系。由图6可以看出，c随着围压的增大呈对数函数降低，而d随围压升高呈线性减小，复相关系数均大于0.99，那么可以定义砂岩在各围压下的初始渗透率为式中：α、β、λ、η为与围压相关的经验常数。

本渗透理论经验模型不仅考虑了孔隙率、泥质含量对砂岩渗透性的影响，还将围压考虑在内，得到了复杂地质条件下砂岩的渗透经验模型。采用式（3）可以预测各地层深度及对应泥质含量、孔隙率下砂岩的渗透率。以围压5MPa为例，图7给出了本次试验所测砂岩渗透率与理论经验模型预测渗透率的对比情况。从图7可以看到，理论预测值与试验值相差较小，表明了本经验模型具有一定的准确性和可靠性。

3.2 模型的扩展

在室内试验应力加载过程中，随着岩石的体积变化，其内部的孔隙率也会发生相应的变化，广泛应用的Kozeny-Carman方程[11]从理论上说明了二者的关系。岩样渗透率随孔隙率变化关系为式中：kz为无量纲常数，取值约为5；∑为单位体积多孔介质内孔隙的表面积；Sp为孔隙介质单位孔隙体积的孔隙表面积。

根据孔隙率的定义可推导出试验过程中孔隙率随体积应变（忽略围压加载引起体积应变的微弱变化量）的变化存在如下关系：式中：φ0为初始孔隙率。

结合式（4）、式（5）可得

因ε<10%， （1+εv）3≈1+εv，故有

结合式（3）、式（7）可得：

式（8）即為考虑应力加载情况下砂岩的渗透率与含泥量、孔隙率、围压及体积应变的关系建立的复杂地质环境下砂岩试验经验扩展渗透模型。

由于破坏时产生的碎屑和泥质颗粒会堵塞部分通道，影响砂岩的渗透特性，因此式（8）只考虑破坏前的渗透变化性。以本文试验砂岩数据为例进行验证分析（以泥质含量为巧%、孔隙率为11.2%及围压为5MPa为例），见图8。从图8可以看到，理论值比试验值稍小，但平均相对误差不到15%，表明本理论模型能够在一定程度上较为准确地预测应力加载下砂岩随体积应变变化的趋势。

4 结论

（1）体积应变扩容点与渗透率的转折突变点相对应，体积应变能较为准确地反映渗透率的变化趋势。

（2）加载偏应力、泥质含量以及孔隙率一定时，砂岩的渗透率随围压的增大而减小；相同应力环境下，砂岩初始渗透率随孔隙率与泥质含量比值的增大呈指数函数增大。

（3）通过试验分析，建立了复杂地质条件下砂岩的经验渗透模型，该模型能较好地预测各地层深度、泥质含量及孔隙率下砂岩的渗透率。

参考文献：

[1]杨吉山，姚文艺，郑明国，等.原状砒砂岩坡面产流产沙规律试验研究[J].人民黄河，2017，39（1）：98-102.

[2]张凌凯，张远芳，刘亮.饱和砂砾土动孔压发展规律试验研究[J].人民黄河，2017，39（2）：136-139.

[3]姜振泉，季梁军.岩石全应力—应变过程渗透性试验研究[J].岩土工程学报，2001，23（2）：153-156.

[4]张守良，沈琛，邓金根.岩石变形及破坏过程中渗透率变化规律的实验研究[J].岩石力学与工程学报，2000，19（增刊1）：885-888.

[5]郭琴，张金功，王永诗，等.泥质岩和泥岩渗透率特征及其影响因素分析[J].兰州大学学报（自然科学版），2008，44（增刊1）：46-48.

[6]张渊，赵阳升，万志军，等.不同温度条件下孔隙压力对长石细砂岩渗透率影响试验研究[J].岩石力学与工程学报，2008，27（1）：53-58.

[7]俞缙，李宏，陈旭，等.渗透压-应力耦合作用下砂岩渗透率与变形关联性三轴试验研究[J].岩石力学与工程学报，2013，32（6）：1203-1213.

[8]王小江，荣冠，周创兵.粗砂岩变形破坏过程中渗透性试验研究[J].岩石力学与工程学报，2012，31（增刊1）：2940-2947.

[9]王连国，缪协兴.岩石渗透率与应力、应变关系的尖点突变模型[J].岩石力学与工程学报.2005，24（23）：4210-4214.

[10]中华人民共和国建设部.工程岩体试验方法标准：GB/T50266-2013[S].北京：中国计划出版社，2013：19-24.

[11]卢平，沈兆武，朱贵旺，等.岩样应力应变全程中的渗透性表征与试验研究[J].中国科学技术大学学报，2002，32（6）：678-684.