梯级泵站输水系统旬优化调度及经济运行研究
吴怡 李智 王京晶 曹悦 雷晓辉
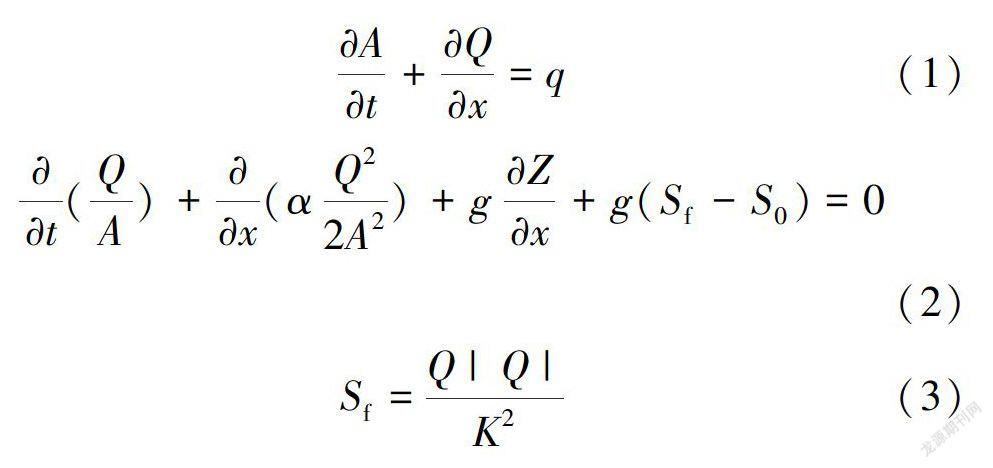
摘要:南水北调来水调入密云水库调蓄工程是北京南水北调配套工程的重要组成部分,该工程后半段从怀柔水库通过3级泵站提升输水至密云水库。为实现该工程高效经济运行,基于北京市分时电价,以怀柔水库至密云水库梯级泵站输水系统运行单位输水成本最小为目标,考虑怀柔水库蓄水量、输水线路水头损失、流量平衡和总扬程等约束条件,采用大系统分解协调模型求解该工程旬内优化调度及经济运行问题。将该大系统分解协调模型分解为梯级泵站扬程优化分配模型和旬优化调度模型2个子系统,采用动态规划法实现各子系统的优化,从而实现大系统的全局优化。应用情况表明:模型具有较好的适用性,可为工程优化调度提供依据,指导工程高效经济运行。
关键词:优化调度;经济运行;梯级泵站;大系统协调分解模型;动态规划法
中图分类号:TV122+.5 文献标志码:A doi:10.3969/j.issn.1000-1379.2018.05.031
南水北调来水调入密云水库调蓄工程是北京南水北调配套工程的重要组成部分,对消纳南水北调来水,弥补水资源亏空,实现北京水资源优化配置具有重要作用。该工程分為团城湖至怀柔水库段(前半段)和怀柔水库至密云水库段(后半段)两段,分别通过6级和3级泵站串联输水。后半段梯级泵站输水系统中间没有调蓄工程,总扬程大,是由泵站、输水线路、闸门等构成的复杂输水系统,其优化调度与经济运行面临着怀柔水库(水源)蓄量、渠道水头损失、流量平衡、总扬程等约束条件。
对于梯级泵站输水系统优化调度与经济运行问题,国内外学者通常将泵站和输水管渠作为整体研究对象,根据系统分析理论,将泵站实际运行参数(或泵站机组性能测算结果)与渠道(或管道)运行水力学特性参数结合起来[1-5],运用遗传算法[6]、动态规划法[7]、粒子群优化算法[8-10]、大系统分解协调法[11]等优化算法进行求解。桑国庆[12]以梯级泵站输水系统为研究对象、中长期运行费用最小为目标函数,综合考虑泵站站前站后水位、输水总量、分时电价等因素,建立梯级泵站系统中长期运行费用优化模型,确定梯级泵站系统中长期运行优化方案。这些研究没有全面考虑分时电价、水源蓄量、输水线路水头损失、流量平衡、总扬程等约束条件,无法直接应用于后半段梯级泵站输水系统优化调配过程。笔者通过建立旬优化调度与经济运行模型,将上述约束条件考虑在内,以后半段梯级泵站输水系统单位输水成本最小为目标,实现该工程的经济运行,最大程度发挥工程效益。
1 研究区域
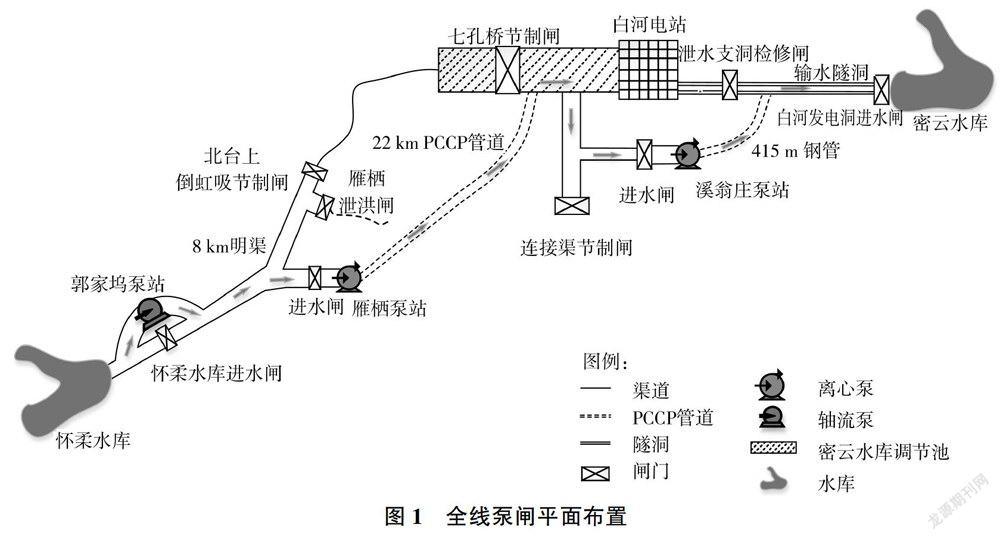
南水北调来水调人密云水库调蓄工程后半段为本次研究区域。怀柔水库在南水北调来水调人密云水库调蓄工程中发挥旬调节功能,最小蓄水量为850万m3,最大蓄水量为1.44亿m3,怀柔水库在调度过程中不允许产生弃水。怀柔水库至密云水库输水线路总长约30km,总扬程114.54m,泵站和闸门等建筑物布置见图1。经怀柔水库调节部分水回补密怀顺水源地,其中一部分对潮白河进行生态补水及向水厂供水;另一部分通过怀柔水库进水闸旁新建的郭家坞泵站提升,经京密引水渠反向输水至北台上倒虹吸,再经新建的雁栖泵站加压,由京密引水渠侧新建DN2600PCCP输水管道人白河电站下游调节池,最后由新建溪翁庄泵站加压后通过白河发电洞将水加压送人密云水库,设计输水流量10m3/s,在实际运行中,输水流量只能为10m3/s或0。
2 数学模型
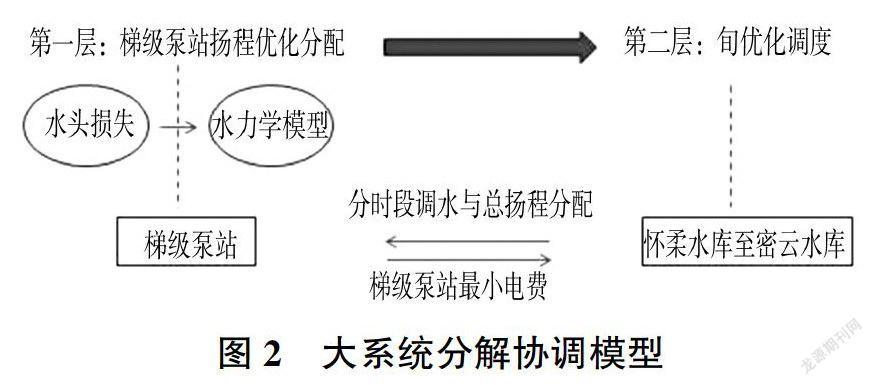
该工程旬优化调度与经济运行问题属于大系统优化问题,采用大系统分解协调模型求解。把该大系统分解成2个子系统,采用动态规划法实现各子系统的优化。根据整个大系统的总目标,考虑各子系统之间的关联,实现大系统的全局优化。大系统分解协调模型见图2,包括2层:第一层为梯级泵站扬程优化分配模型,将总扬程在梯级泵站之间进行分配,使得梯级泵站运行费用最小,其中水头损失通过建立一维水力学模型求得;第二层为旬优化调度模型,优化怀柔水库调度过程,使得梯级泵站输水系统单位输水成本最小。
2.1 一维水力学仿真模型
针对梯级泵站输水系统的特点,构建一维非恒定流水力学仿真模型,基于仿真模型,对泵站、倒虹吸、渐变段等复杂的内部构筑物进行概化处理,并将概化的内部构筑物与圣维南方程组进行耦合,同时采用稳定性好、计算精度高的四点时空偏心Preissmann格式对方程组进行离散,用高效率的双扫描法求解。在此基咄上采用恒定非均匀流计算模块对研究区恒定流和非恒定流进行模拟,从而进行渠道水力学特性分析和梯级泵站优化[13]。输水线路非恒定流计算采用一维圣维南方程组,该方程组由连续性方程和动量方程组成:式中;A、Q为断面面积和流量;x、t为空间和时间坐标;q为单位长度渠道上的侧向入流流量;α为动量修正系数;Z为水位;g为重力加速度;Sf为水力坡度;S0为渠道底坡;K为流量模数。
2.2 梯级泵站扬程优化分配模型
最后一级泵站站后水位减去第一级泵站站前水位可得到梯级泵站系统净扬程,加上由水力学模型计算得到的各渠段水头损失即可得到总扬程[14]。在满足各渠段水力联系、各级泵站站前站后水位约束等条件下,进行梯级泵站扬程分配,使梯级泵站耗能最小。这是一个总扬程在梯级泵站之间分配的空间优化问题。将所研究的问题赋予时间特性,即将泵站按顺序编号,把每级泵站作为一个阶段,该优化问题就变成了一个多阶段决策过程的优化问题,可以采用动态规划技术来求解。
(1)阶段变量。将泵站编号作为阶段变量j(j=1,2,…,m),其中m为投入运行的泵站数(本研究中m取3)。
(2)状态变量。将第j阶段至最末阶段m的累计扬程作为状态变量。式中:sj为第j阶段至最末阶段m的累计扬程(状态变量);Hi为第i阶段的扬程;i为编号。
(3)决策变量。将每级泵站的扬程Hj作为决策变量。对于决策变量的离散化,离散的步长越小,计算精度越高,但计算量显著增加。
(4)状态转移方程。状态转移方程表示梯级泵站中第j+1阶段(即第j+1个泵站)状态变量Sj+1和第j阶段(即第j个泵站)状态变量Sj与决策变量Hj之间的关系。
Sj+1=Sj-Hj(5)式中:S1=H*(H*为梯级泵站总扬程);Sm+1=0。
(5)目标函数。对于梯级泵站,考虑各泵站的电费,其目标函数为式中:Qj为第j个泵站的出水流量;ηj为第j个泵站在Qj、Hj组合工况下的效率;△t为梯级泵站运行时间,取24h;c为日平均电价;ρ为水的密度。
(6)约束条件。总扬程约束:
单级泵站扬程约束:
Hjmin≤Hj≤Hjmax(8)式中;Zm为最后一级泵站站后水位;Z0为第一级泵站站前水位;hj,j+1为相邻两级泵站间输水线路的水头损失,由水力学模型计算得出;Hjmin、Hjmax为第j级泵站的最小、最大扬程。
站前站后水位约束:每一级泵站的站前站后水位都要在控制范围内。
(7)求解方法。采用逆向递推、正向决策法计算,递推方程为
Fm+1(Sm+1)=0(9)
Fj*(Si)=min[Lj(Si,Hj)+Fj+1*(Sj+1)](10)式中:Fm+1(Sm+1)为最末阶段结束时的电费;Lj(Si,Hj)为第j阶段的费用函数;Fj*(sj)为第j阶段的最小费用函数。
2.3 旬优化调度
根据怀柔水库来水和回补地下水、供水、生态补水需求,在工程各约束条件下,优化旬调度过程,使得梯级泵站输水系统单位输水成本最小。采用动态规划法描述此模型。
(1)阶段变量。阶段变量采用k(k=1,2,…,N)表示,将1旬分为N个时段,即N天。
(2)状态变量。将怀柔水库每时段初的蓄水量Vk作为状态变量。
(3)决策变量。将每时段怀柔水库的调水流量Qk作为决策变量。
(4)状态转移方程。由水量平衡可得状态转移方程:
Vk+1=Vk+(Q1In+Q2In-Q1Out-Q2Out-Q3Out)×86400-Qk×Δtk(11)式中:Q1In为天然来水流量;Q2In为团城湖来水流量;Q1Out为怀柔水库向水厂供水流量;Q2Out为回补地下水流量(密怀顺地下水源地,设计要求为10m3/s);Q3Out为生态补水流量; Qk为日平均调水流量Δtk为第k天的调水时间。
此外,可通过Vk查水位库容曲线得到第k天的怀柔水库水位。
(5)目标函数。目标函数为式中:Qk,j,p为第k天第p时段第j座泵站的流量,实际运行中为10m3/s或0;Hk,j为第k天第j座泵站的扬程;η(k,j)为第k天第j座泵站的效率;△tp为某天第p
(6)约束条件。怀柔水库蓄水量约束:Vmin≤Vk≤Vmax,Vmin和Vmax分别为怀柔水库的最小和最大蓄水量;流量平衡约束:Qk,j,p=Qk;效率约束:η(k,j)≠0;扬程约束和水位约束同前所述。
(7)求解方法。采用逆向递推、正向决策法计算,递推方程为
FN+1(VN+1)=0(13)
Fk*(Vk)=min[Lk(Vk,Qk)+Fk+1*(Vk+1)](14)式中:FN+1(VN+1)為最末阶段结束时的电费;Lk(Vk,Qk)为k阶段的费用函数;Fk*(Vk)为k阶段的最小费用函数。
2.4 优化结果
第一级泵站(郭家坞)站前水位为怀柔水库水位,由水量平衡求出旬调度过程逐日蓄水量,反查水位库容曲线得到怀柔水库逐日水位且认为一天内不变;最后一级泵站(溪翁庄)站后水位为密云水库水位,认为一旬内不变。根据工程实际运行需求,基于北京市现行分时电价,将1d概化为3个调度时段,即7:00至15:00、15:00至23;00和23;00至次日7;00,电价分别为1.1412、1.0205、0.3818元/(kW·h)。
假设怀柔水库在某一旬(10d)的调度过程中,团城湖向怀柔水库输水流量为20m3/s,怀柔水库天然来水流量为20m3/s,回补密怀顺水源地流量为10m3/s,供水流量为18m3/s,生态补水流量为5m3/s,怀柔水库初、末水位均为58m,密云水库水位为132m。为方便计算,以及使计算结果便于运行管理,泵站扬程离散步长为0.1m,假设每天调水小时数为整数,一旬中每天调水时间前9d为16h,第10d为24h,前9d的调水时间为15:00至次日7:00、第10d全天输水。
怀柔水库水位见图3,可知旬内怀柔水库水位变化很小,最大不足4cm。由水力学仿真模型计算出输水线路水头损失为0.35m,可认为旬内总扬程为定值,从而计算出郭家坞、雁栖和溪翁庄泵站旬内的扬程分别为2.3、33.8、48.4m,3个泵站运行效率分别为0.698、0.900、0.900。由此得出旬调水总量为604.8万m3,总电费为942605元,单位输水成本为0.1559元/m3。
3 结论
针对南水北调来水调入密云水库调蓄工程怀柔水库至密云水库段工程特点,考虑怀柔水库蓄水量约束、输水损失、流量平衡、梯级泵站总扬程等约束条件,以梯级泵站输水系统单位输水成本最小为优化目标,基于北京市分时电价,采用大系统分解协调模型分层建立旬优化调度与经济运行模型,包括梯级泵站扬程优化分配模型和旬优化调度模型,并运用动态规划法求解,其中输水线路水头损失由一维水力学模型计算。分层结构模型具有较大的灵活性和适应性,各子模型单独优化计算,层层递进,可以保证达到全局最优。从优化结果可以看出,一旬内怀柔水库水位变化较小,各泵站每天运行时间内扬程和效率均不变,且梯级泵站优先在电价低的时候运行,保证单位输水成本最小。
参考文献:
[1]严登丰.泵与泵装置特性预测[J].排灌机械工程学报,2012,30(3):315-323.
[2]贾仁甫,王红,金明宇,等.调水工程中梯级泵站的优化调度研究[J].扬州大学学报(自然科学版),2006,9(2):69-73.
[3]MORADI-JALAL M,MARINO M A,AFSHAR A.OptimalDesign and Operation of Irrigation Pumping Stations[J].Journal of Irrigation and Drainage Engineering,2003,129(3):149-154.
[4]RODIN S I.Use of Genetic Algorithms for Optimal Control ofBulk Water Supply[J].Journal of Irrigation and DrainageEngineering,2004,130(5):357-365.
[5]PULIDO-CALVO I,ROLDANJ,L6PEZ-LUQUE R,et al.Demand Forecasting for Irrigation Water Distribution Systems[J].Journal of Irrigation and Drainage Engineering,2003,129(6):422-431.
[6]SAVIC D A,WALTERS G A,SMITH M R,et al.Cost Sav-ings on Large Water Distribution Systems:Design ThroughGenetic Algorithm Optimization[C]//Proceedings of JointConference on Water Resource Engineering and Water Re-sources Planning and Management.Minneapolis,Minnesota:ASCE,2000:1-10.
[7]COSTA B E,ALMEIDA R A,VIANA A N C.Optimizationof Parallel Variable-Speed-Driven Centrifugal Pumps Operation[J].Energy Efficiency,2008(3):167-173.
[8]OSTFELD A,TUBALTZEV A.Ant Colony Optimization forLeast-Cost Design and Operation of Pumping Water Distribu-tion Systems[1].Journal of Water Resources Planning andManagement,2008,134(2):107-118.
[9]吳月秋,纪昌明,王丽萍,等.基于混沌粒子群算法的水电站水库优化调度[J].人民黄河,2008,30(11):96-112.
[10]赵晓军,田富强,胡和平.粒子群优化算法在水量调度方案优化中的应用[J].人民黄河,2005,27(11)26-27.
[11]朱劲木,龙新平,刘梅清,等.东深供水工程梯级泵站的优化调度[J].水力发电学报,2005,24(3):123-127.
[12]桑国庆.基于动态平衡的梯级泵站输水系统优化运行及控制研究[D].济南:山东大学,2012:142-149.
[13]张大伟.南水北调中线干线水质水量联合调控关键技术研究[D].上海:东华大学,2014:11-32.
[14]刘波波.梯级泵站调水工程优化运行模拟研究[D].北京:北京工业大学,2015:59-61.

