Banach空间上有关紧凸集的Hausdorff度量拓扑的若干性质*

杨 鎏

(陕西学前师范学院 数学系,西安 710100)

超空间是无限维拓扑的经典研究对象.Hausdorff 建立拓扑空间后不久,Vietoris在20世纪20年代开始了超空间的研究.至20世纪70年代,Curtis-Schori-West超空间定理的出现,标志着超空间理论的基本成熟[1-5].继经典的超空间定理之后,国内外许多学者在超空间理论中又做了很多有意义的工作.例如国内学者杨忠强和日本学者SAKAI K[3,6]研究了底空间为局部紧的度量空间的超空间的拓扑结构.2007年,文献[7]又开始考虑Banach空间中闭凸集的超空间.实际上证明了n维欧氏空间Rn中所有非空闭凸集赋予Fell拓扑所构成的超空间同胚于R×Q;n=1时同胚于R×I,其中Q=[-1,1]ϖ,I=[0,1].杨忠强还把超空间理论和函数空间理论结合起来,研究了连续函数空间下方图形的超空间拓扑结构[8-9].实际上,其在超空间理论和函数空间理论进行了大量深刻而系统的研究[10-16].有关无限维拓扑学函数空间理论的详细基础知识,可参考文献[17].

底空间为线性空间的超空间拓扑结构研究,代表性论文源于1979年[18],考虑了局部凸的可度量空间紧凸集的超空间的拓扑结构.文献[19-20]研究了Banach空间上非空闭凸集的全体赋予Hausdorff度量,其超空间连通分支的拓扑结构,Banach空间超空间在广义Hausdorff度量下其度量分支的拓扑结构.本文将给出Banach空间上Hausdorff度量的若干性质,以及对偶空间上的性质.

1 超空间上的Hausdorff度量拓扑

对于度量空间(X,d),(Y,ρ), 记C(X,Y)上的一致收敛拓扑为τuc[21],则C(X,Y)上存在一个自然的无限值的相容的一致超度量duc,

定义1 设CL(X)表示空间X的所有非空闭集构成的集族,A∈CL(X),B∈CL(X).则A,B之间的Hausdorff距离dH(A,B)定义为

关于CL(X)上的Hausdorff度量拓扑,有以下的描述.

定理1 设X是一个度量空间.则CL(X)上的Hausdorff度量拓扑τuc[22]使得：

对每个A∈CL(X),

ed(A,·):(CL(X),τHd)→[0,],

ed(·,A):(CL(X),τHd)→[0,],

Dd(A,·):(CL(X),τHd)→[0,],

均为τHd连续的CL(X)上最弱的拓扑.其中

ed(A,B)=sup{d(a,B):a∈A},

Dd(A,B)=inf{d(a,B):a∈A}.

由超出函数和间隙函数所决定的弱拓扑实际上可诱导出超空间上的各种拓扑,例如度量空间上的Vietoris拓扑,Attouch-Wets拓扑等等.相关的更多结果可参考文献[21,23-24].

利用定理1,可将Hausdorff距离表示成以下的等价形式:

dH=max{ed(A,B),ed(B,A)}

=inf{ε>0|A⊆Nd(B,ε),B⊆Nd(A,ε)}

2 Banach空间上紧凸集的Hausdorff度量拓扑的性质

设cc(X)表示空间X的所有非空紧凸集构成的集族.

命题1A,B,C,D∈ccH(X) 且λ∈C.则

①dH(A,{0})=sup{‖a‖:a∈A}.

②dH(λA,λB)=|λ|dH(A,B).

③dH(A+C,B+D)≤dH(A,B)+dH(C,D).

④dH(conv(A∪B),conv(C∪D))≤max{dH(A,C),dH(B,D)}. 其中conv表示其凸包.

⑤ 如果t,s∈[0,1], 则dH((1-t)A+tB,(1-s)A+sB)≤|t-s|dH(A,B).

证明①,②显然.

③ 只要说明dH(A+C,B+C)≤dH(A,B)即可,因为

dH(A+C,B+D)≤dH(A+C,B+C)+dH(B+C,B+D)≤dH(A,B)+dH(C,D)

而dH(A+C,B+C)≤dH(A,B)是显然的,因对任意的a+c∈A+C,其中a∈A,c∈C,存在b∈B使得d(a+c,b)≤dH(A,B)所以d(a+c,b+c)=d(a,b)≤dH(A,B).反之对任意的b+c∈B+C也同样能找到a∈A使得d(b+c,a+c)≤dH(A,B),由此得证.

④ 设r=max{dH(A,C),dH(B,D).对任意的x∈conv(A∪B),则存在t∈[0,1]及a∈A,b∈B使得x=ta+(1-t)b.则

d(x,conv(C∪D))=d(ta+(1-t)b,conv(C∪D))=d(ta+(1-t)b,tconv(C∪D)+(1-t)conv(C∪D))≤d(ta,tconv(C∪D))+d((1-t)b,(1-t)conv(C∪D))≤d(ta+(1-t)b,tp+(1-t)q)≤d(ta,tp)+d((1-t)b,(1-t)q)=td(a,p)+(1-t)d(b,q)≤tdH(A,C)+(1-t)dH(B,D)≤tr+(1-t)r=r

其中p,q分别为C,D中的点.

同理,对任意的y∈conv(C∪D),可证d(y,conv(C∪D))≤r.

⑤ 因为

(1-t)A+tB=(1-t)A+sB+(t-s)B,

(1-s)A+sB=(1-t)A+sB+(t-s)A,

再利用性质④即可得证.

证明dH((1-t)A+tB,

(1-s)A+sB)≤|t-s|dH(A,B).

对任意的x∈(1-t)A+sB,

设x=(1-t)a+tb,

则d(x,(1-s)A+sB)≤d((1-t)a+tb,

(1-s)a+sb)≤d((1-t)a,

(1-s)a)+d(tb,sb)=(t-s)‖a‖+(t-s)‖b‖≤(t-s)(‖a‖+‖b‖)≤(t-s)dH(A,B)

同理对任意的y∈(1-s)A+sB,可证d(y,(1-t)A+tB)≤|t-s|dH(A,B).故对任意的t,s∈[0,1],dH((1-t)A+tB,(1-s)A+sB)≤|t-s|dH(A,B).

3 Banach空间的对偶空间上有关紧凸集的Hausdorff度量性质

设X是Banach空间,X*′是它的实对偶空间,X*′是它的复对偶空间.

记ccH(X)表示集族cc(X)上赋予Hausdorff度量拓扑.

对任意的C∈cc(X).令C*={x*∈X*| supx*(C)<∞}.记SX*={x*∈X*:‖x*‖=1}.有下面的命题.

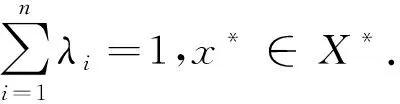
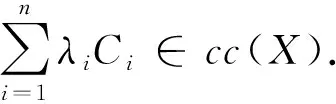
②A=B当且仅当对每个x∈X*有

x*(A)=x*(B).

③dH(x*(A),x*(B))≤‖x*‖dH(A,B).等价地有,对每个x*∈SX*,都有dH(x*(A),x*(B))≤‖x*‖dH(A,B),显然映射x*:ccH(X)→ccH(C)是连续的.

② 若A≠B,则不妨设存在a∈A但a∉B.由凸集分离定理知,存在x*∈X*′,γ1,γ2∈R使得对所任意的b∈B,Rex*(a)<γ1<γ2

③ 因A,B是紧集,故存在λa∈x*(A),λb∈x*(B),使得ρ(λa,λb)=ρH(x*(A),x*(B))

则相应地存在两点a∈A,b∈B使得λa∈x*(a),λb∈x*(b).则ρH(x*(A),x*(B))=|x*(a)-x*(b)|=|x*(a-b)|≤‖x*‖|a-b|,显然ρH(x*(A),x*(B))≤‖x*‖dH(A,B).

命题3 设A,B∈cc(X),x∈X*′则

|max{Rex*(a)|a∈A}-max{Rex*(b)|b∈B}|≤dH(x*(A),x*(B))=‖x*‖dH(A,B)

证明：由于A,B是X中的紧凸集,且x*连续,故存在实数a1,a2,b1,b2使得

Rex*(a)=[a1,a2],Rex*(b)=[b1,b2].

则|max{Rex*(a)|a∈A}-max{Rex*(b)|b∈B}|=|a2-b2|≤max{|b1-a1|,|b2-a2|}=dH([a1,a2],[b1,b2])≤dH(x*(A),x*(B))≤‖x*‖dH(A,B).

4 结 论

本文借助于底空间较特殊的Banach空间,运用其代数性质(如具有线性性质,完备性,对偶性等),借助一般拓扑学,泛函分析中的方法研究并证明了Banach空间上赋予Hausdorff度量拓扑构成的超空间的代数性质,有助于研究者更深刻地认识整个超空间中各个对象之间的相互作用,以及一些特殊的凸集对超空间拓扑结构的影响,从而更好地研究 Banach 空间上有关凸集的超空间问题.