混合反射表面下SFS三维形貌重建方法研究*

王国珲，吴二星

(西安工业大学 光电工程学院，西安 710021)

明暗重建形貌(Shape From Shading，SFS)是计算机视觉中重建物体三维形貌的关键方法之一[1]，也是光度学领域中一个重要的研究方向，其原理是利用图像的明暗变化获取物体表面各点的法向向量，进而由法向向量通过积分重建三维形貌[2].SFS方法仅利用摄像机采集物体表面的单幅图像，设备简单，适应性强，应用非常广泛[1].

SFS方法最初是由MIT的学者Horn[2]对月球表面进行三维形貌重建时提出的.文献[3-5]认为，SFS算法大致可分为四类：线性化反射图法[6]、局部分析法[7]、最小化能量法[2,8]以及偏微分方程法[1,9].各种SFS算法存在一定的优点，也不可避免地存在不足之处.线性化反射图法虽计算速度较快，但基于反射图函数中低阶项起主导作用的假设，故求解过程缺乏可信度，并且由于求解结果只是近似解，因此重建误差较大；局部分析法对满足局部形状的特定物体表面重建效果较好，但使用范围受到限制，且由于表面的局部形状假设与实际形状之间通常存在偏差，故重建精度不高；最小化能量法需要引入各种约束条件，且约束条件可能导致重建结果失真等；偏微分方程法多数情况下需考虑边界条件，重建精度较高[4]，目前来讲是一种较为理想的算法.

大多数文献[1-7,9]中SFS方法假定物体表面的反射特性服从Lambert定律，即物体表面对入射光的反射在任意方向上的辐射亮度恒定不变，但事实上，这个条件过于理想并不总是满足.为此，许多学者开始专注于非Lambert表面的SFS三维形貌重建.文献[10]提出了一个含有镜面反射的统一反射图模型，将物体表面用三角形面元来近似，通过线性化反射图和最小化能量函数得到物体表面的高度；文献[11]研究了基于Oren-Nayar反射模型的非Lambert漫反射物体的SFS问题；文献[12]研究了基于Ward反射模型的SFS图像辐照度方程，使用Lax-Friedrichs sweeping方法对建立的图像辐照度方程进行了求解；在文献[11]研究的基础上，文献[13]将semi-Lagrangian方法用于建立非Lambert表面图像辐照度方程的求解，取得了较好的重建效果.文献[14]基于文献[12]的研究结果，使用Oren-Nayar模型代替Ward反射模型中的漫反射部分，设计了基于fixed-point迭代sweeping方法用于求解上述模型建立的图像辐照度方程[14].然而，文献[10]由于没有直接对建立的SFS图像辐照度方程进行求解，且算法属于线性化反射图法和最小化能量法，故三维重建精度较低；文献[12,14]建立了基于偏微分方程法的图像辐照度求解算法，但是由于Ward反射模型的复杂性，数值算法中很难找到一个最优的人工黏性因子；文献[13]尽管可以获得较好的效果，但将其用于混合反射表面SFS图像辐照度方程的求解实现起来异常复杂.

为此，本文提出了一种基于Schlick模型的混合反射表面SFS三维形貌重建方法.在正交投影且光源与摄像机方向一致情况下，对SFS方法进行了建模.详细阐述了混合反射表面下基于Blinn反射模型的图像辐照度方程的建立，Schlick模型对Blinn反射模型的改进，图像辐照度方程的转化与求解等，并通过实验对提出的SFS方法进行了验证.

1 基于Blinn反射模型的图像辐照度方程

建立如图1所示的笛卡尔直角坐标系，设摄像机的光轴与z轴重合，摄像机的成像平面为x-y平面.在上述坐标系下，物体表面三维形貌某点(x,y,z(x,y))处的单位法向量表达式为

n(x,y)=(p(x,y),q(x,y),-1)/

(1)

式中：p(x,y)=∂z(x,y)/∂x,

q(x,y)=∂z(x,y)/∂y.

在正交投影条件下，SFS三维形貌重建方法即为求解如下的图像辐照度方程[2]，即：

I(x,y)=R(p(x,y),q(x,y))

(2)

式中：I(x,y)为图像的灰度值；R(p(x,y),q(x,y))为由反射模型确定的反射图函数.

对理想的Lambert漫反射表面，反射特性服从Lambert定律，即物体表面对入射光的反射在任意方向上的辐射亮度恒定不变，其反射图函数为

R(p(x,y),q(x,y))=n(x,y)·L

(3)

式(3)表明了理想的Lambert漫反射表面其反射图分布仅仅和n与光源方向向量L之间的夹角有关.然而，对于实际的物体表面，往往既含有漫反射又含有镜面反射的混合反射表面.为此，文献[15]提出了如下反射模型来计算混合反射表面的反射图分布，表达式为

R(p(x,y),q(x,y))=kd(n(x,y)·L)+

ks(n(x,y)·H)N

(4)

式中：H为L与摄像机方向向量V的夹角平分线的单位方向向量，即H=(L+V)/2；N为镜面反射指数；kd、ks分别为漫反射、镜面反射成分的加权因子，通常kd+ks≤1.

图1 SFS方法中的坐标系

将式(4)带入式(2)，可以得到基于Blinn反射模型的图像辐照度方程为

I(x,y)=kd(n(x,y)·L)+

(5)

由于n(x,y)·L=cosθi，n(x,y)·V=cosθr，带入式(5)可得

(6)

式中：θi、θr分为物体表面法向量n与光源方向向量L、摄像机方向向量V之间的夹角.

2 Schlick模型的图像辐照度方程

在光源与摄像机方向一致情况下，有θi=θr.设光源的方向向量L为(0,0,-1)，故有

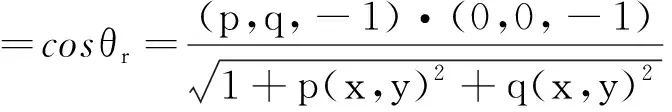
(7)

则基于Blinn反射模型的图像辐照度方程(式(6))变为

(8)

图像辐照度方程(式(8))是一个一阶非线性偏微分方程.当镜面反射指数N≥3时，求解较为困难且求解过程繁琐.

为解决式(8)的求解问题，本文使用文献[16]提出的改进的Blinn反射模型，即Blinn模型中镜面反射成分用下式来代替，即

(9)

N*I(x,y)f2-[(N-1)I(x,y)+N*kd+ks]f+(N-1)kd=0

(10)

基于Schlick模型的图像辐照度方程(式(10))是关于f的一元二次方程.求解该方程可得

(11)

进一步可以发现(式(10))实质上是一个Eikonal类偏微分辐照度方程，即：

(12)

式中：Ω为给定的图像区域；g(x,y)为定义在∂Ω上的边界条件.

3 偏微分辐照度方程求解

为了求解式(12)，本文利用文献[17-19]中提出的一阶和高阶差分格式对式(12)的解进行了逼近，并应用fast sweeping方法对算法迭代过程进行了加速.

3.1 一阶差分格式

文献[17]证明了通过迭代的方式，利用单调迎风Godunov格式逼近‖z(x,y)‖可以收敛到式(12)的解，即

(13)

(14)

将z1、z2和式(14)带入式(13)，可得：

(15)

求解式(15)，且满足单调迎风条件，得到逼近解zi,j，即物体表面的三维形貌为

(16)

3.2 高阶差分格式

对于p-、p+和q-、q+来说，为了构造具有高阶精度的数值方法，需要计算其高阶差分，可利用文献[18]中提出的三阶加权本质无振荡(Weighted Essentially Non-Oscillatory，WENO)格式进行计算.式(12)的高阶差分格式为

(17)

式中：

(18)

式中：

(19)

式中：

(20)

求解式(17)，可迭代得到逼近解zi,j，即物体表面的三维形貌为

(21)

3.3 Fast sweeping方法

为了加速算法收敛，应用文献[19]提出的fast sweeping方法对算法迭代过程进行了加速.当计算导数p-、p+以及q-、q+时，使用最新得到的z值，同时sweeping不只从一个方向进行，而是从以下四个方向交替重复进行：① 从左上到右下；② 从左下到右上；③ 从右下到左上；④ 从右上到左下.根据不同的sweeping方向，zi±1,j、zi±2,j、zi,j±1、zi,j±2需要取不同的值.

本文提出的算法步骤为：

2) Sweeping：在第n+1步，使用迭代式(16)或式(21)对zi,j进行更新.同时，sweeping过程从以下四个方向进行：① 从左上到右下，即i=1∶m,j=1∶n；② 从左下到右上，即i=m∶1,j=1∶n；③ 从右下到左上，即i=m∶1,j=n∶1；④ 从右上到左下，即i=1∶m,j=n∶1.

3) 迭代停止准则：当‖zn+1-zn‖L1≤ε，算法停止迭代，否则返回步骤2).其中‖·‖为定义在L1上的范数；ε>0为收敛阈值，本文取ε=10-5.

4 仿真结果与分析

为验证混合反射表面下SFS重建方法的有效性，利用半球和花瓶图像进行了仿真实验，并将高阶方法重建结果与一阶方法重建结果进行了对比.

4.1 半球图像的三维重建

半球图像可使用球体函数生成，即：

(22)

式中：(x,y)∈[-63,64]×[-63,64]；R=50为半球的半径，由式(22)可以得到半球的三维形貌

真实值.

图2为半球图像的仿真实验结果，三维图中的所有单位均为像素.图2(a)是使用半球函数(式(22))且基于Blinn反射模型(式(6))生成的半球的灰度图像，其中Blinn模型的参数kd=0.85、ks=0.15、N=90.从图2(a)中可以看出，半球灰度图像为混合反射表面的成像效果，因为在灰度图像的中央区域存在着较强的镜面反射成分.图2(d)为一阶方法重建值图2(c)与三维形貌真实值图2(b)之间的误差图，图2(f)是高阶方法重建值图2(e)与三维形貌真实值图2(b)之间的误差图.从图2(c)和图2(e)中可以看出，本文提出的一阶方法和高阶方法均可得到较为理想的重建结果.从图2(d)和图2(f)中可以看出，本文提出的高阶方法重建误差比一阶方法重建误差小.

图3为半球图像三维形貌真实值(图2(b))、一阶方法重建值(图2(c))及高阶方法重建值(图2(e))的中心横截面的比较结果，从图3中可以看出，高阶方法重建值比一阶方法重建值更接近三维形貌真实值，误差更小，这是由于高阶方法使用了高阶精度的三阶WENO差分格式.

图2 半球图像的三维形貌重建结果

图3 半球图像三维形貌重建结果的中心横截面

4.2 花瓶图像的三维重建

花瓶图像可使用花瓶函数生成，即：

(23)

式中:f(x)=0.15-0.025(2x-1)(3x-2)2(2x+1)2(6x+1)；(x,y)∈[-0.5,0.5]×[-0.5,0.5].将x，y映射到区间[-63,64]，同时将高度z(x,y)扩大128倍，此时花瓶的最大高度

值为36.55.同样，花瓶的三维形貌真实值也可以得到.

图4为花瓶图像的仿真实验结果，三维图中的所有单位均为像素.其中，图4(a)是使用花瓶函数(式(23))且基于Blinn反射模型式((6))生成的花瓶的灰度图像，其中Blinn模型的参数同图2保持一致：kd=0.85、ks=0.15、N=90.从图4(a)可以看出，花瓶灰度图像亦为混合反射表面的成像效果，因为在灰度图像的中央区域也存在着较强的镜面反射成分.图4(d)为一阶方法重建值图4(c)与三维形貌真实值图4(b)之间的误差图，图4(f)为高阶方法重建值图4(e)与三维形貌真实值图4(b)之间的误差图.从图4(c)和图4(e)可以看出，本文提出的一阶方法和高阶方法均可得到较为理想的重建结果.从图4(d)和图4(f)可以看出，本文提出的高阶方法重建误差比一阶方法重建误差小.上述所得到的结论与图2得到的结论一致.

图4 花瓶图像的三维形貌重建结果

图5为花瓶图像三维形貌真实值(图4(b))、一阶方法重建值(图4(c))及高阶方法重建值(图4(e))的中心横截面的比较结果，从图5中也可以看出，高阶方法重建值比一阶方法重建值更接近三维形貌真实值，误差更小，这也是由于高阶方法使用了高阶精度三阶WENO差分格式.

4.3 三维重建结果分析

为了定量地比较重建结果，使用高度平均绝对误差(Mean Absolute Error，MAE)和均方根误差(Root Mean Square Error，RMSE)来对一阶方法和高阶方法重建结果进行比较，MAE和RMSE表达式分为

(24)

(25)

图5 花瓶图像三维形貌重建结果的中心横截面

灰度图像一阶方法MAERMSE高阶方法MAERMSE半 球1.818 01.961 71.112 21.163 0花 瓶1.569 01.668 60.967 41.032 9

由图2～5和表1所示的半球、花瓶图像的三维形貌重建结果以及高度MAE和RMSE误差可以得出,本文提出的一阶方法和高阶方法均可以获得较好的重建效果，且与一阶方法相比，高阶方法可获得较高的重建精度，其高度MAE和RMSE误差降低了大约38%.

5 结 论

本文提出了一种基于Schlick模型的混合反射表面SFS三维形貌重建方法，旨在解决混合反射表面下SFS重建方法中建立的偏微分辐照度方程难以求解的问题.在以摄像机光轴为z轴，成像平面为x-y平面建立的笛卡尔直角坐标系和正交投影条件下，推导了基于Blinn反射模型的混合反射表面下的反射图函数，构建了基于Blinn模型的图像辐照度方程；在光源与摄像机方向一致情况下，使用Schlick模型代替原Blinn反射模型中的镜面反射成分，将辐照度方程转化为关于三维形貌梯度的二次方程，求解此方程可获得Eikonal类偏微分方程；利用一阶Godunov和高阶WENO差分格式对辐照度方程的解进行了逼近，并应用fast sweeping方法对算法迭代过程进行了加速.一阶方法和高阶方法均可以获得较好的重建效果，且与一阶方法相比，高阶方法可获得较高的重建精度.下一步研究将重点围绕透视投影下混合反射表面SFS方法的快速、高精度求解等内容展开.