层状ZnO纳米材料的储氢性能研究*

张宁超，任 娟，张苗苗，王 鹏

(1.西安工业大学 电子信息工程学院,西安 710021;2.西安工业大学 理学院,西安 7100213.西北机电工程研究所，咸阳 712099)

ZnO具有宽带隙(室温下为3.37 eV)和较大的激子束缚能(60 meV)，是重要的半导体材料.由于ZnO特殊的电子、光学等性质使其被广泛应用于气体传感器、发光二极管、太阳能电池和光探测器等方面[1-4].近几年来，纳米线、纳米团簇、纳米带及纳米管等ZnO纳米材料相继诞生，这些材料由于尺寸效应的影响，因其不同于晶体表现出高的比表面积和大的孔隙率的特殊性质，将成为新型的储氢材料.因此，研究ZnO纳米的储氢特性，将其广泛应用于新能源方面[5-6]具有重要意义.

文献[7]采用密度泛函的理论方法首次预言ZnO纳米单层结构的存在.文献[8]通过X射线衍射和扫描隧道显微镜观察到了在基底Ag上合成的ZnO纳米单层，为后续研究ZnO纳米单层更多性质提供了实验数据的支撑.由于ZnO纳米单层同石墨烯、层状的BN结构一样，均有比较高的比表面积，该物理特性表明层状ZnO纳米材料可以用于氢气的储存，并成为一种新的储氢材料.文献[9]首先利用热力学计算的方法，研究了单层ZnO上氢气分子的覆盖率，发现在298 K和5 MPa的条件下，ZnO纳米单层的储氢质量分数为1.5%～2.1%.但其研究没有通过温度和压力的变化获得ZnO纳米单层更为丰富的储氢数据，对于层状ZnO纳米的储氢也没有深入研究，热力学计算得到的结果精确性也有待进一步讨论.本文利用第一性原理计算方法，在分析ZnO纳米单层类石墨烯结构特征的基础上，使用层状ZnO纳米吸附氢气的性能.分别采用密度泛函理论计算和巨正则蒙特卡罗方法(Grand Canonical Montte Carlo,GCMC)模拟对层状ZnO纳米结构在不同温度和压力下的储氢性能进行计算模拟和分析.

1 计算模型与方法

本文中所研究的ZnO纳米单层结构是从纤锌矿ZnO晶体结构上沿(0001)面“切”下一层，计算过程中构建了一个二维的超胞，该超胞包含32个原子.对氢气分子在ZnO不同吸附位的研究通过密度泛函理论，采用密度泛函半核芯赝势(DFT Semicore Pseudopotential,DSPP)[10]处理相对效应，选取了包含p轨道极化函数的双数值轨道基组.在优化过程中，所有结构不受对称性的约束，以达到最终的稳定结构.结构优化和能量计算的自洽场(Self Consistent Field,SCF)自洽能收敛精度为1.0×10-5Hartree，原子所受最大力为0.002 Hartree·(Å)-1，轨道截断半径设置为4.5 Å.层状ZnO纳米框架结构储氢量的模拟采用巨正则蒙特卡洛方法[11]，吸附剂的势参数采用DREIDING力场中的Zn和O原子的参数，氢气分子在模拟过程中采用双原子模型，其势能参数采用文献[12]的参数结果(σH=2.72 Å,εH/kB=10.00 K,dH-H=0.74 Å).模拟过程所构建的超胞，x方向为19.496 Å，y方向为16.884 Å，z方向是层间距H的变化.

2 结果与讨论

2.1 ZnO纳米单层与H2分子的相互作用

ZnO纳米单层同石墨烯一样，均具有高的比表面积.本文使用ZnO纳米单层结构研究了其吸附氢气的性能.如图1所示，分别给出了氢气分子位于a吸附位：O原子顶部；b吸附位：Zn原子顶部；c吸附位：六元环的中央；d吸附位,桥位1；e吸附位:桥位2.吸附能计算由公式Eb=E(host)+E(H2)-E(host+H2)定义，E(host)表示ZnO纳米单层体系总能量，E(host+H2)表示ZnO纳米单层吸附氢气后的总能量，E(H2)表示单个氢气分子的能量.在不同吸附位的吸附能见表1.

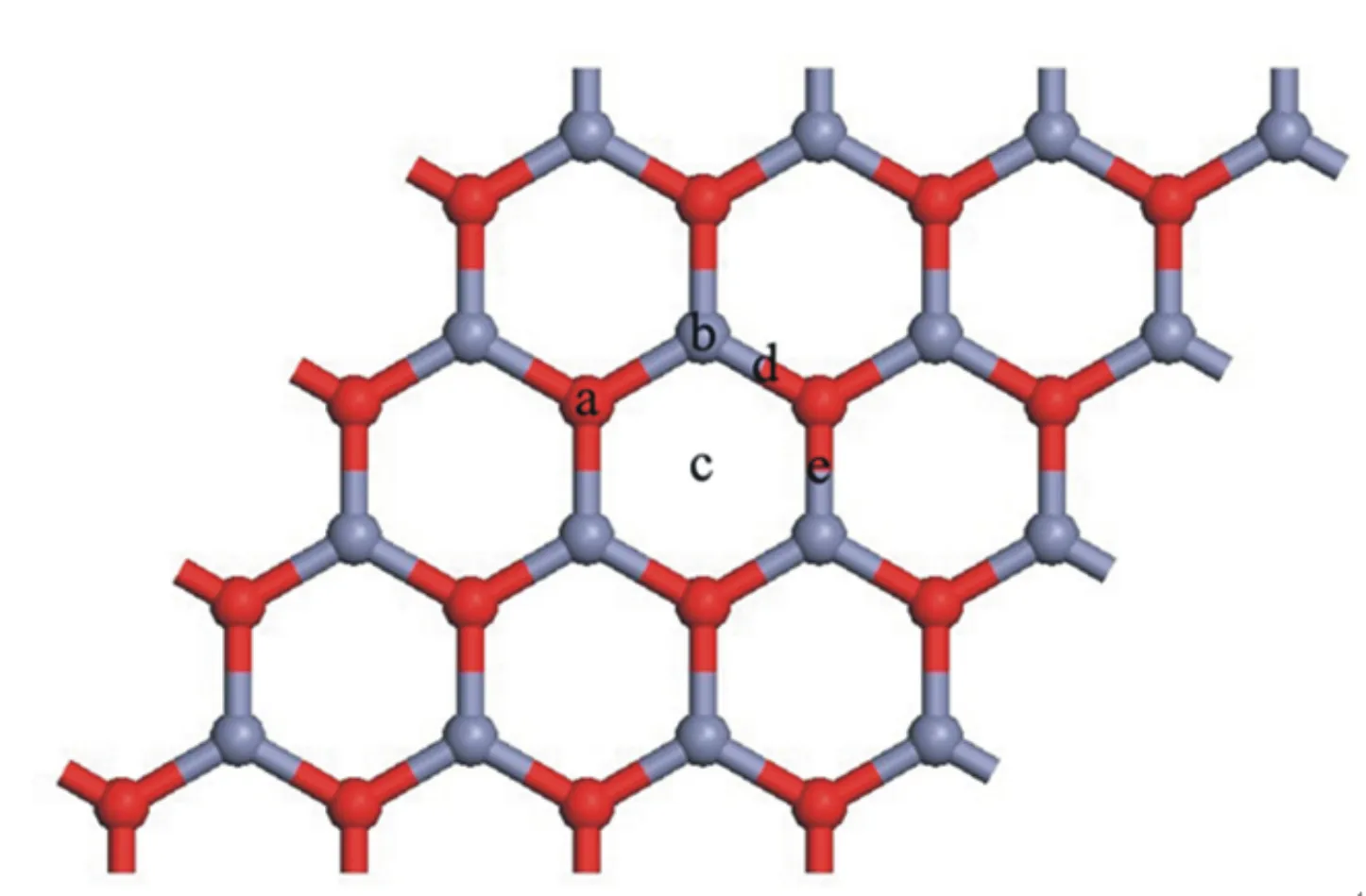
图1 ZnO纳米单层结构及氢气分子不同吸附位

已有的研究表明采用局域密度近似(Local Density Approximation,LDA)交换相关项偏小估计吸附能，而采用广义梯度近似(Generalised Gradient Approximation,GGA)略大估计吸附能.本文分别采用LDA和GGA的方法计算了氢气分子在不同吸附位的吸附能.计算的结果表明采用LDA计算的吸附能平均值为0.16 eV，而GGA计算的结果为0.26 eV.由此可以判断氢气分子在ZnO纳米单层上的吸附能介于0.16～0.26 eV之间，属于弱的物理吸附.

表1 氢气分子在ZnO纳米单层上不同吸附位的吸附能Tab.1 The absorption energy of different sites of hydrogen molecules on ZnO monolayer

图2给出了氢气分子在ZnO纳米单层上不同的吸附位的结构图.图2(a1)～2(e1)是氢气分子放置的初始位置图，图2(a2)～2(e2)是弛豫后的结构图.

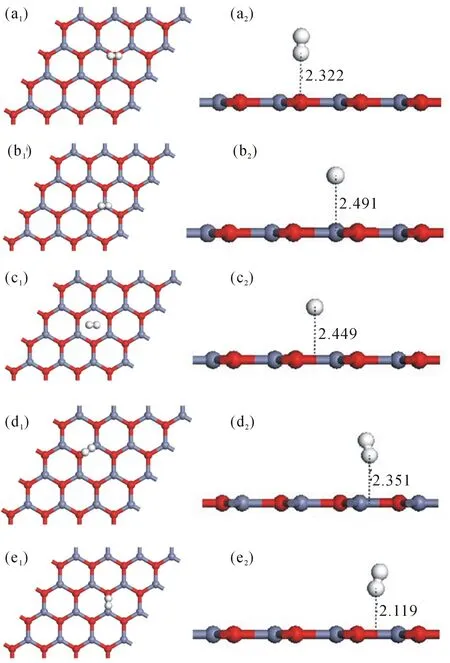
图2 氢气分子在ZnO纳米单层上不同的吸附位的结构图

如图2所示H2分子在不同吸附位的初始位置均是平行于ZnO平面.结构弛豫后，结果显示氢气分子不再这样整齐排列，最近的氢原子到平面的距离依次为：a吸附位(2.322 Å)、 b吸附位(2.491 Å)、c吸附位(2.449 Å)、d吸附位(2.351 Å)和e吸附位(2.119 Å).而且a、b、d、e吸附位的氢气分子弛豫后均向c吸附位靠近，表明六元环的中心位置(c吸附位)是最佳吸附位置.

2.2 层状ZnO纳米储氢性能的GCMC模拟

使用GCMC方法模拟了层状ZnO纳米的吸附等温线，结果如图3所示，随着层间距H的变化，储氢质量分数也发生变化.层间距H分别选取H=5.414 Å、6.414 Å、7.414 Å、8.414 Å、9.414 Å、12.90 Å、15.00 Å、18.00 Å、25.00 Å.图3中，在温度分别为T=293 K和T=77 K时，GCMC模拟的层状ZnO纳米的吸附等温线，压强范围为0.001～20 MPa.图3(a)表示在室温下，层间距为H=5.414 Å，从吸附等温线上判断几乎没有氢气分子进入层状ZnO纳米结构中.随着层间距的增大，开始有氢气分子进入到框架结构中.层间距为H=6.414 Å、P=4 MPa 时，储氢质量分数ω为0.24%，当压强增大到P=20 MPa 时，储氢质量分数为0.46%.层间距为H=18 Å 时，在压强为P=4 MPa、10 MPa和20 MPa时，储氢质量分数分别为 0.25%，0.53%和0.85%.同时研究了层间距直至25 Å时，层状ZnO纳米框架的一个储氢情况.层间距为H=25 Å，P=4 MPa、10 MPa和20 MPa时，储氢质量分数分别为0.30%，0.66%和1.10%.从吸附等温线及以上的数据分析发现，除层间距为H=5.414 Å以外所研究的层间距结构，在P≤4 MPa时，储氢质量分数没有太大的变化，不论层间距是6.414 Å还是25 Å.由此可以判断在低压区域，孔表面对于储氢量起主要作用，与孔洞的大小没有关系.但是随着压强的增大，不同的层间距储氢量有明显的差异，特别是层间距H=25 Å，储氢量随着压强的增大快速增长.所以在高压区，孔洞的大小对于储氢量起关键作用.如图3(b)所示，采用同样的方法研究了层状ZnO纳米在液氮温区的储氢性能.在T=77 K时，储氢质量分数明显提高.层间距为H=5.414 Å，P=4 MPa时，储量质量分数为0.65%.随着层间距的增大，储氢量依次增大.层间距H=18 Å时，在压强为P=4 MPa、10 MPa和20 MPa时，对应的储氢质量分数分别为2.44%，2.92%和3.25%.并且发现，层间距为H=5.414 Å、6.414 Å、7.414 Å、8.414 Å和9.414 Å的框架结构，在低压区域，储氢量增速很快，到了P=2.5 MPa之后，吸附等温线基本平行于压强轴，吸附量基本已经达到饱和，随着压强的增大，储氢量不再有明显的提高.层间距为H=25 Å，随着压强的增大储氢量增大，大的层间距可以有更多的空间“容纳”氢气分子，直到压强增大到20 MPa时，储氢量还有增大的空间.

图3 0.001～20 MPa压力区间层状ZnO材料的吸附等温线

Fig.3 Absorption isotherms of H2in the interlayer of ZnO sheets at (a) 298 K and (b) 77 K,respectively,in the range from 0.001 to 20 MPa

3 结 论

1) 六元环结构的单层ZnO纳米，单个氢气分子在六元环的中心位置结合能达到最大.

2) 层状ZnO纳米在室温下层间距H=6.414 Å，压强P=4 MPa时氢气分子开始进入框架结构，而且储氢量随着压强的增大快速增长，随着温度的降低而增长.

3) ZnO较多的电子数导致材料本身比较重，影响了储氢量，可通过掺杂过渡金属改变材料特性，从而获得层状ZnO纳米材料更优异的储氢性能.