2018年浙江省数学高考第21题的解析与思考*

●

(萧山区第五高级中学,浙江 杭州 311202)

图1

2018年高考落下帷幕，在不断深化发展的课改中，浙江省数学高考试题的题型、知识考查点、难易分布等也在不断变化.“不落俗套”或许是高考选拔人才的一个重要指标，2018年浙江省数学高考试题第21题就是这样一道题——既注重基础知识考查，又注重能力选拔；既回归解析几何本质，又“不按常理”出牌.笔者尝试从知识考查、解法探究与拓展研究等方面对该题进行分析与探讨.

例1如图1，已知点P是y轴左侧(不含y轴)一点，抛物线C：y2=4x上存在两个不同的点A，B满足PA，PB的中点均在C上.

1)设AB的中点为M，证明：PM⊥y轴；

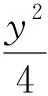
(2018年浙江省数学高考试题第21题)

1 题意分析

本题给出的是y轴左侧任意一点P，过点P作抛物线的两条弦PA和PB，恰PA，PB的中点均在抛物线上.第1)小题是一个定值问题的证明，貌似是证垂直，实则是证点P，M的纵坐标相等；第2)小题是当点P在定曲线上运动时，研究相应三角形面积的取值范围.第1)小题为第2)小题作铺垫.

两个小题的解决具有一定难度，有别于我们对解析几何常规的认知：通常解析几何的问题先是设动直线方程(引入参数斜率k)，联立方程，使用韦达定理，然后寻找已知与未知的联系，等等.本题第1)小题虽然是我们并不陌生的一个中点问题，但因为条件中给的是PA，PB的中点均在抛物线上，所以比较难运用上述的“常规方法”,可转化为韦达定理解决.稍加分析后可以发现，问题的解决仍是以解析几何基本思想为基础，已知点在曲线上，则该点坐标符合曲线方程；条件中的点A，B及PA，PB的中点均在抛物线上，因此这4个点坐标符合抛物线方程，然后再寻找条件与结论的关系.