二次曲线的若干优美性质*
——2018年全国卷Ⅰ解析几何试题引发的思考
●
(黄石市第一中学,湖北 黄石 435000)
2018年全国数学高考卷Ⅰ(文、理科)的解析几何试题有一个共同特点:已知定点P(m,0)是圆锥曲线C:F(x,y)=0内一点,过点P的动直线与圆锥曲线C相交于点A,B,则存在点Q,使得∠AQP=∠BQP.
1 试题呈现

1)当l⊥x轴时,求直线AM的方程;
2)设O为坐标原点,证明:∠OMA=∠OMB.
(2018年全国数学高考卷Ⅰ理科试题第19题)
例2设抛物线C:y2=2x,点A(2,0),B(-2,0),过点A的直线l与C交于点M,N.
1)当l⊥x轴时,求直线BM的方程;
2)证明:∠ABM=∠ABN.
(2018年全国数学高考卷Ⅰ文科试题第20题)
2 引发思考
上述两道试题的第2)小题难度都不大,例1的第2)小题只需要证明kMA+kMB=0,即可知直线
MA,MB的倾斜角互补,从而∠OMA=∠OMB;例2的第2)小题只需要证明kBM+kBN=0,即可知直线BM,BN的倾斜角互补,从而∠ABM=∠ABN.具体解答过程此处略.
尽管圆锥曲线的模型不同,但是有着类似的结论,值得我们深入思考.例1和例2的第2)小题解答后,笔者产生了3个疑惑(以例1为例):
1)如何知道存在使等角恒成立的定点M呢?如果要求点M的坐标,那么该怎么办?
2)既然椭圆和抛物线有类似结论,那么圆和双曲线是否也有类似的结论?能否得到圆、椭圆、双曲线和抛物线的一般性结论?
3)上述两道高考试题中的直线经过的定点都在曲线内部,如果定点在曲线外部,那么结论又如何?
3 结论推广
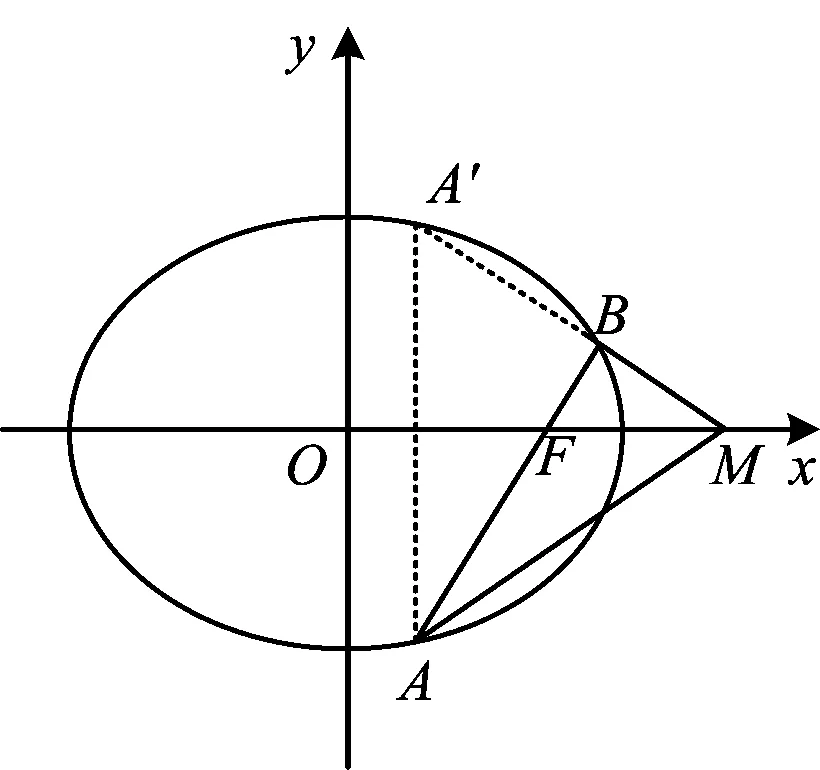
图1

圆、椭圆、双曲线和抛物线都是对称的二次曲线,很多时候它们有着相同的性质.下面,我们带着上述3个疑惑进行探究,试着将此结论向圆、椭圆、双曲线和抛物线进行推广.
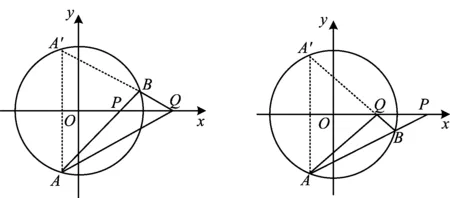
图2 图3

证明设A(x1,y1),B(x2,y2),点A关于x轴的对称点为A′(x1,-y1),设直线AB:x=ky+m,则直线A′B的方程为
(x2-x1)(y+y1)=(y2+y1)(x-x1).
令y=0,得

(k2+1)y2+2kmy+m2-r2=0,
依题意有Δ>0,则
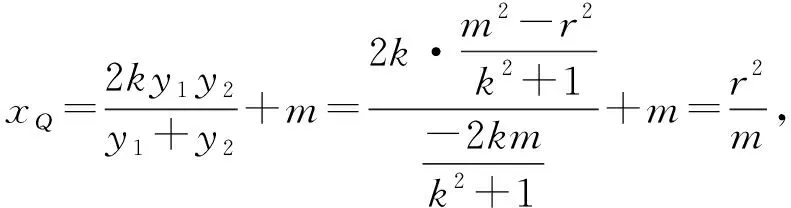


证明设A(x1,y1),B(x2,y2),Q(x0,0),直线AB:x=ky+m,则∠AQP=∠BQP等价于
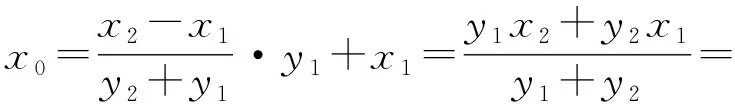


(k2+1)y2+2kmy+m2-r2=0,
依题意有Δ>0,则

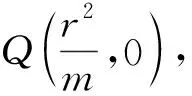
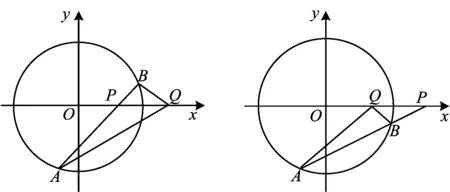
图4 图5

证明同推论1,这里不再赘述.
值得说明的是:当定点P(m,0)在⊙O内时,∠AQP=∠BQP;当定点P(m,0)在⊙O外时,∠AQP+∠BQP=180°.
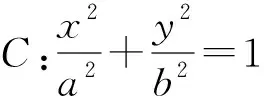
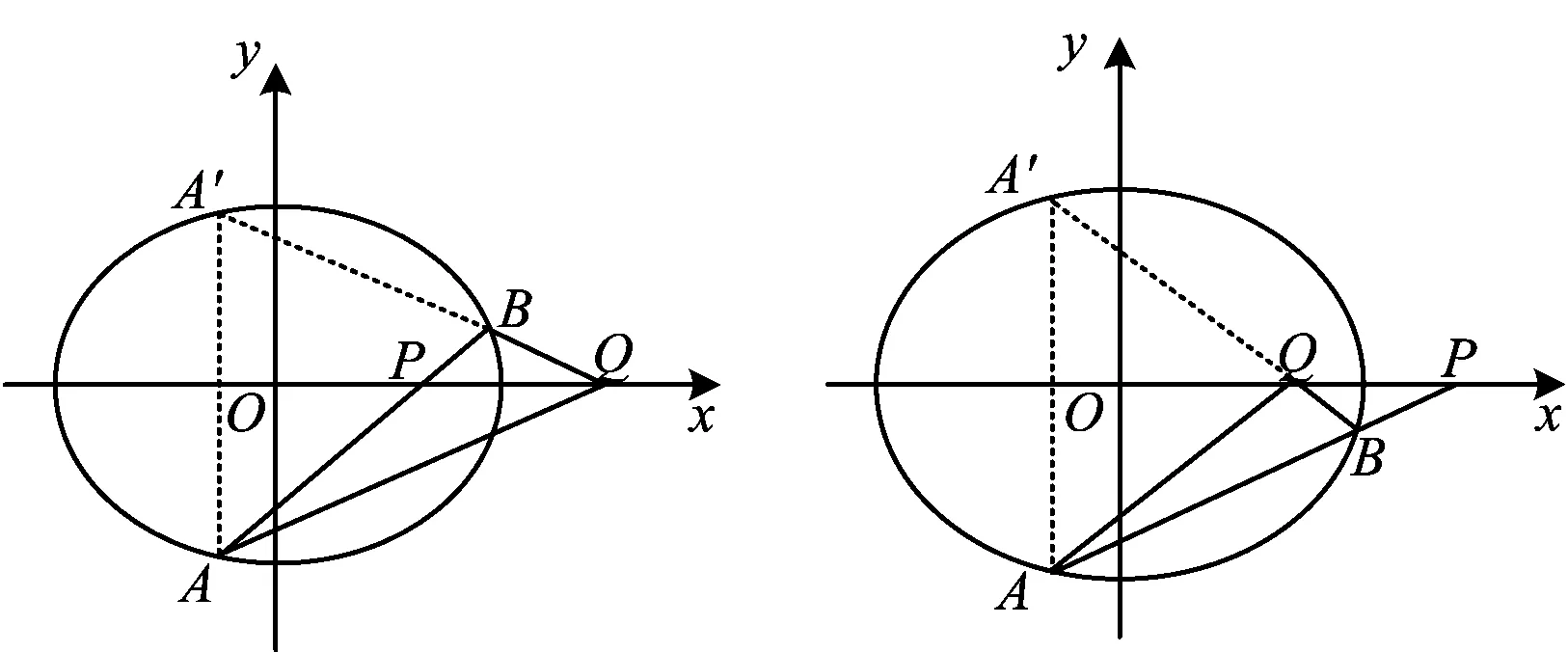
图6 图7
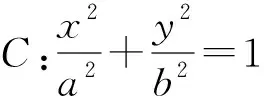
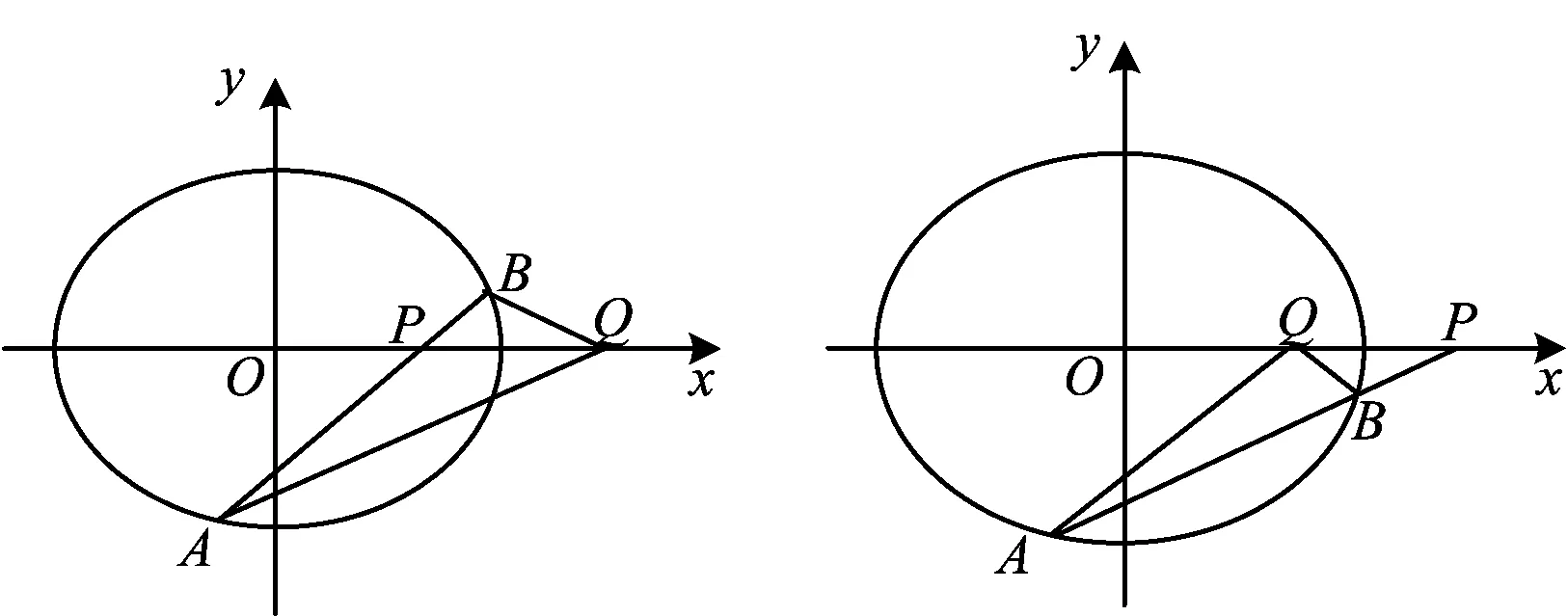
图8 图9
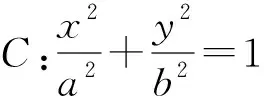
证明同推论1,这里不再赘述.
值得说明的是:当定点P(m,0)在椭圆C内时,∠AQP=∠BQP;当定点P(m,0)在椭圆C外时,∠AQP+∠BQP=180°.




推论5和推论6的证明可仿照推论1、推论3,此处不再赘述.
值得说明的是:当定点P(m,0)在双曲线C内时,∠AQP=∠BQP;当定点P(m,0)在双曲线C外时,∠AQP+∠BQP=180°.
定理4已知抛物线C:y2=2px(其中p>0),过定点P(m,0)(其中m≠0)的动直线l与抛物线C相交于点A,B,点A关于x轴的对称点为A′,则直线A′B过定点Q(-m,0).
证明设A(x1,y1),B(x2,y2),点A关于x的对称点为A′(x1,-y1),设直线AB:x=ky+m,则直线A′B的方程为
(x2-x1)(y+y1)=(y2+y1)(x-x1),
令y=0,得
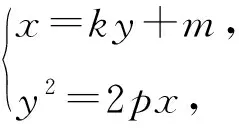
y2-2pky-2pm=0,
其中Δ=4p2k2+8pm>0,则
y1y2=-2pm,y1+y2=2pk,
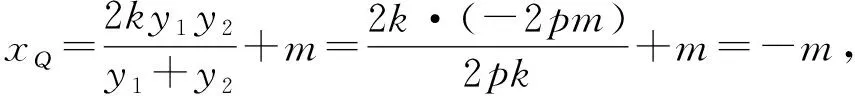
因此直线A′B过定点Q(-m,0).
推论7已知抛物线C:y2=2px(其中p>0),过定点P(m,0)的动直线l与抛物线C相交于点A,B,则存在点Q(-m,0),使得∠AQP=∠BQP.
推论8已知抛物线C:y2=2px(其中p>0),过定点P(m,0)(其中m<0)的动直线l与抛物线C相交于点A,B,则存在点Q(-m,0),使得∠AQP+∠BQP=180°.
推论7和推论8的证明可仿照推论1、推论3,此处不再赘述.
值得说明的是:当定点P(m,0)在抛物线C内时,∠AQP=∠BQP;当定点P(m,0)在抛物线C外时,∠AQP+∠BQP=180°.
下面给出一般性结论:

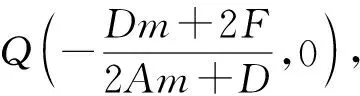
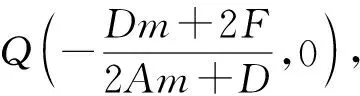
推论9和推论10的证明同上.
值得说明的是:当定点P(m,0)在二次曲线Γ内时,∠AQP=∠BQP;当定点P(m,0)在二次曲线Γ外时,∠AQP+∠BQP=180°.

