深度透视2018年全国数学高考卷Ⅰ理科第16题*
●
(虞阳中学,福建 福清 350307)
近年来高考试题的命制越来越新颖多变,但万变不离其宗,大多数高考题都能在教材或往年高考真题中找到其“原形”.高考对三角最值的考查也不例外,通过背景包装、更换数字、变条件、变结论等多种方式对教材的例题、习题以及高考真题进行重新加工,看似平常,实则有很多值得品位的东西.现以2018年全国卷Ⅰ理科试题第16题为例,从解法探究、寻根探源、同源变式等角度来欣赏它,从而轻松突破求三角最值问题的思维瓶颈.
例1已知函数f(x)=2sinx+sin 2x,则f(x)的最小值是______.
(2018年全国数学高考卷Ⅰ理科试题第16题)
该题表述简洁,考查的内容丰富,主要考查二倍角公式、同角三角函数的基本关系式以及利用导数判断函数的单调性求最值或利用基本不等式的推论求最值等基础知识,意在考查考生的转化和化归能力、运算求解能力,考查逻辑推理、数学运算、直观想象等核心素养.在近5年的全国卷中,求三角函数的最值在2017年卷Ⅱ理科第14题、2017年卷Ⅲ文科第6题、2014年卷Ⅱ文(理)科第14题都出现过,这些题多利用二倍角公式、两角和差的正余弦公式以及辅助角公式对三角函数进行化简,再利用三角函数的单调性,即可求其最值.本题若不会利用导数法或基本不等式的推论,则即使会利用三角公式进行化简,也求不出最值.这样设制高考题规避了特殊技巧,凸显了数学本质,能有效地考查考生的创新意识.
1 解法探究
解法1因为
f(x)= 2sinx+sin 2x=2sinx(1+cosx)=
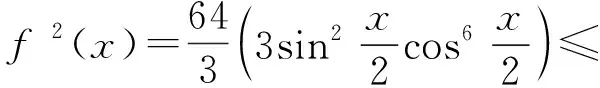
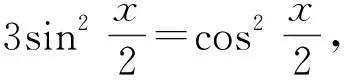
于是

点评本解法的关键:一是“化简”,即利用二倍角的正弦公式与余弦公式,对三角函数的解析式进行化简;二是“用推论”,即利用基本不等式的推论,求出三角函数的最值,此时需注意等号成立条件的检验.
解法2因为f(x)=2sinx+sin 2x=2sinx(1+cosx),所以
f2(x)= 4sin2x(1+cosx)2=
4(1-cosx)(1+cosx)3≤
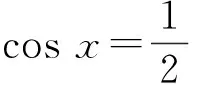
于是

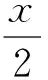
解法3因为f(x)=2sinx+sin 2x=2sinx(1+cosx),所以
f2(x)= 4sin2x(1+cosx)2=
4(1-cosx)(1+cosx)3.
设y=f2(x),cosx=t,则
y=4(1-t)(1+t)3(其中-1≤t≤1),
从而y′= 4[-(1+t)3+3(1-t)(1+t)2]=
8(1+t)2(1-2t),
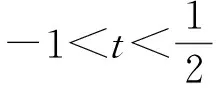
即
进而

点评本解法的关键:一是“会化简”,只需用二倍角公式与同角三角函数的基本关系式,把f2(x)化为同角同名的函数式;二是“会换元”,即通过三角换元,把三角函数转化为四次函数,此时需注意利用余弦函数的有界性,求出新元的取值范围;三是“用导数”,即对函数求导,利用导数的符号,判断函数的单调性,求出其最值,从而得到f2(x)的最值,即可求出f(x)的最小值.
解法4因为f(x)=2sinx+sin 2x,所以
f′(x)=2cosx+2cos 2x=4cos2x+2cosx-2.
设y=f′(x),cosx=t,则
y= 4t2+2t-2(其中-1≤t≤1),

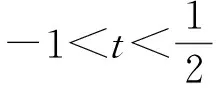
点评与前3种解法相比,本解法跳过对函数f(x)的三角化简,直接对函数f(x)求导,再通过三角换元(注意新元的取值范围),判断导函数的符号,直接求出f(x)的最小值,实属干净利落.
解法5因为f(x)=2sinx+sin 2x,所以
f(x+2π)= 2sin(x+2π)+sin 2(x+2π)=
2sinx+sin 2x=f(x),
从而2π是函数f(x)的周期,于是欲求函数f(x)=2sinx+sin 2x的最小值,等价于求函数f(x)=2sinx+sin 2x(其中0≤0≤2π)的最小值.求导得
f′(x)= 2cosx+2cos 2x=
4cos2x+2cosx-2=
其中0≤x≤2π.令f′(x)=0,得
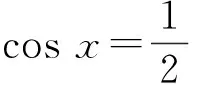
即

由于
f(π)=0,f(0)=0,f(2π)=0,

点评本解法的关键:一是“会转化”,即利用周期函数的定义,判断三角函数的周期性,把求函数f(x)在定义域R内的最小值转化为求函数f(x)在[0,2π]上的最小值;二是“用导数”,即求方程f′(x)=0的根,求出根所对应的函数值与端点的函数值,比较大小得函数f(x)在闭区间上的最值.
2 寻根探源
本题来源于人教A版教材第147页复习参考题A组第11题的第1)小题[1]:
例2已知函数f(x)=2sinx(sinx+cosx),求f(x)的最大值.

3 同源变式
思考1若把例1中的“函数f(x)=2sinx+sin 2x”变为“f(x)=2sinx+sin2x”,其他都不变,即可得到如下难度降低的好题:
变式1已知函数f(x)=2sinx+sin2x,则f(x)的最小值是______.
分析设t=sinx(其中-1≤t≤1),则
y=t2+2t,
即
y=(t+1)2-1.
当-1≤t≤1时,函数y=t2-4t+5单调递增,从而当t=-1时,函数y=t2+2t(其中-1≤t≤1)取得最小值ymin=-1,即f(x)的最小值是-1.
点评求形如y=acos2x+bcosx+c或y=asin2x+bsinx+c(其中a,b,c,d均为常数,且ab≠0)的函数最值,常用三角换元法,将所给的函数化成最值容易确定的另一个函数.一般可设t=cosx(其中-1≤t≤1)或t=sinx(其中-1≤t≤1),再利用配方法,判断函数的单调性,即可求出原函数的最值.但在换元时应注意等价性,即关注新元的取值范围.
思考2若把例1中的“函数f(x)=2sinx+sin 2x”变为“f(x)=2sin2x+sin 2x”,其他都不变,即可得到如下难度降低的好题:
变式2已知函数f(x)=2sin2x+sin 2x,则f(x)的最小值是______.
分析因为f(x)=2sin2x+sin 2x,所以
f(x)= 1-cos 2x+sin 2x=

点评破解此类三角函数最值问题的关键:一是化简三角函数的解析式,化简的目标为“角化同”(如本题,优先考虑“幂降一次角翻倍”,即先把“2sin2x”转化为“1-cos 2x”,再利用辅助角公式,把函数f(x)转化为形如f(x)=Asin(ωx+φ)+h的形式);二是利用正弦函数的最值性,即可求出三角函数的最值.
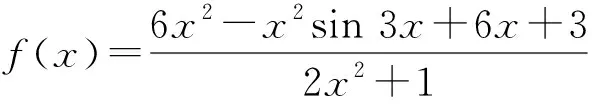
变式3已知函数
则f(x)的最小值与最大值之和为______.
分析因为

M+m=(3-M′)+(3-m′)=6-(M′+m′)=6.
所以函数g(x)为奇函数.设g(x)的最大值和最小值分别为M′,m′,则M′+m′=0.设函数f(x)的最大值为M,最小值为m,则
点评破解此类题的关键:一是巧妙变形,对所给函数的解析式进行适当变形;二是巧构函数,根据函数的解析式所具有的明显特征,巧妙构造函数;三是活用性质,即活用奇函数的性质,奇函数的图像关于原点对称,即可轻松求出最值.
从以上3个角度可窥:对典型高考题从不同角度进行变式探究,是深化知识、提升能力的重要途径.

