再探“等弧度三圆共点图”*

●

(温州市教育教学研究院,浙江 温州 325000)

笔者曾在本刊发表了题为“‘等弧度三圆共点图’的几个有趣性质”和“‘等弧度三圆共点图’中一个神奇的四点共圆”两篇文章，给出了等弧度三圆共点图的许多有趣性质.本文将继续探究等弧度三圆共点图并进一步揭示其内在的数学性质，给出一系列有趣的四点共圆.

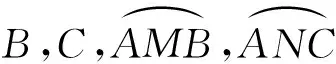
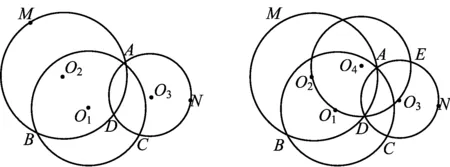
图1 图2

文献[1]揭示了“黄圆图”中隐含的一个漂亮的四点共圆：

性质1在“黄圆图”中，点O1，O2，O3，D共圆.

文献[2]又给出性质1中的四点共圆存在一个美妙的性质：

本文将继续探究“等弧度三圆共点图”中内在的性质，给出一系列有趣的四点共圆.

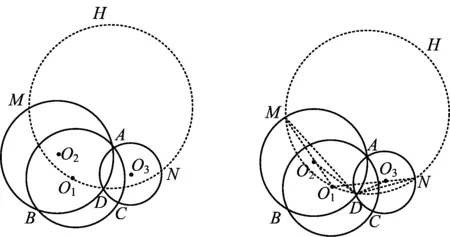
图3 图4

证明联结MO1，NO1，O2D，O3D，MD，ND(如图4)，显然MO1经过点O2，NO1经过点O3，根据性质1可知，点O2，O1，D，O3共圆，从而

∠DO2O1=∠DO3O1.

又因为∠DO2O1=2∠MDO2，∠DO3O1=2∠NDO3，所以

∠MDO2=∠NDO3，

从而

图5 图6

先给出一个结论：

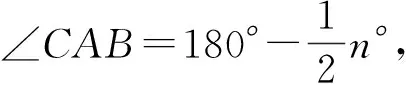
∠MAB+∠CAN+∠CAB=180°，

即点M，N，A共线.

下证点A，E，F，H共线.联结AF，AE，FN，EM，延长AE交⊙O1于点H′(如图7).由FN，EM分别是⊙O3，⊙O2的直径，知FA⊥MN，EA⊥MN，从而点A，E，F共线.又

∠H′AB=∠BAM=∠CAH′+∠CAN=90°，

于是

∠H′AB=∠CAH′，

图7 图8

∠M+∠MED=∠N+∠NFD=90°，

得

∠MED=∠NFD,

故点O1，E，D，F共圆，从而

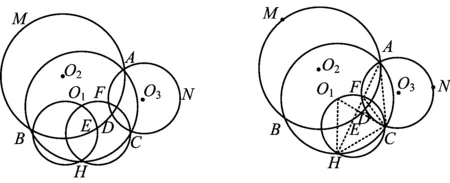
图9 图10

证明先证点O1，H，C，F共圆.

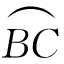
即

∠HO1C=∠HFC,

因此，点O1，H，C，F共圆，从而

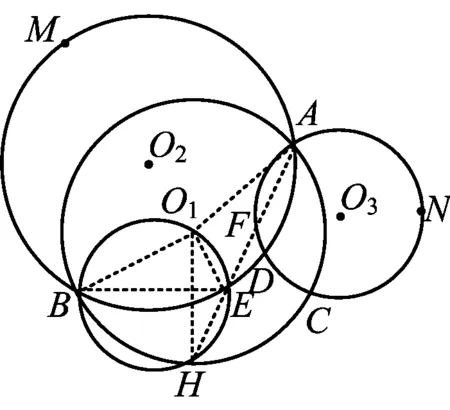
图11

△BO1E≌△AO1E, ∠B=∠A.

而O1H=O1A，于是∠A=∠H，得∠B=∠H，因此，点O1，B，H，E共圆.由

又

△BO1H≌△CO1H，

故经过点O1，H，C，F的圆与经过点O1，B，H，E的圆是等圆.

图12

关于这个“黄圆图”，肯定还有许多有趣的性质，有待数学爱好者继续研究(见文献[1-3]).下面我们再给出“黄圆图”的一个性质，限于篇幅，其证明不再赘述，留给读者完成.

1)⊙O2，⊙O3与大圆O1分别内切于点M，N;