线性规划类试题的命题思路演变与新视角*

●

(大厂高级中学,江苏 南京 210044)

如果两个变量x，y满足一组一次不等式，求这两个变量的一个线性函数(例如z=2x+y)的最大值或最小值，那么我们就称这个线性函数为目标函数，称一次不等式组为约束条件，像这样的问题叫作二元线性规划问题.

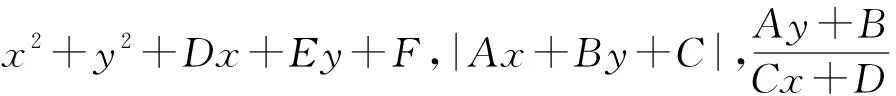
1 加减变乘除，对数来还原

线性运算指加法和数量乘法，在实数领域中只包含加法和数量乘法的二元一次方程就属于线性运算，如y=2x+1.在线性规划问题中，无论是约束条件还是目标函数都只有加法和数量乘法这两种运算.利用指数式和对数式的关系，将对数间的线性运算隐藏于指数式的乘除关系中，不失为一种同时考查学生转化能力的命题视角.

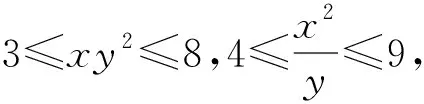
(2010年江苏省数学高考试题第12 题)

分析由条件知x>0，y>0.对两个不等式均取以10为底的对数，得

lg 3≤lgx+2lgy≤lg 8，

lg 4≤2lgx-lgy≤lg 9，

此时

问题等价于设x，y为实数，满足

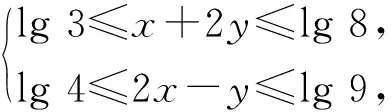
求3x-4y的最大值.

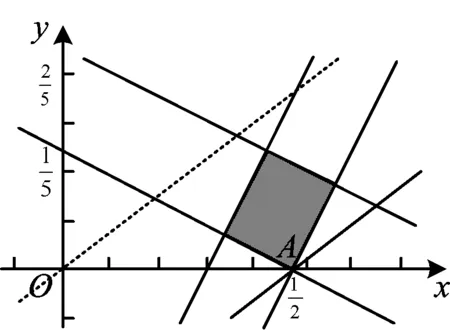
图1

画出不等式组表示的可行域(是一个矩形)，如图1.令z=3x-4y，即

zmax=3lg 3=lg 27,

评注通过取对数，代数式的乘(方)除运算可以转化为对数的加减运算，实现非线性运算向线性运算的转化.需要注意的是，当约束条件和目标函数都是代数式的乘(方)除运算时，只有同时对它们取对数，才能借用线性规划的思想求解.类似地，同底幂的乘(方)除运算就是指数间的线性运算，从运算转化的视角也可以命制相应的试题.

2 目标非线性，画出曲线看

在线性规划问题中，线性目标函数被理解为坐标系中的一条直线，观察其在与可行域有公共点的前提下纵截距(含z的式子)的几何意义.循此思路，目标函数是曲线同样可以观察其几何意义——选择合适的视角.

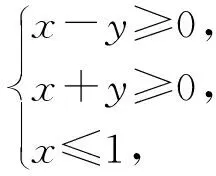
图2

当它的图像过点A(1，1)时，z取得最大值，故

评注目标函数是非线性函数，z+1为曲线与y轴交点的纵坐标，以这个几何意义为依据确定最优解.循此思路命题：画好一个可行域(如例2中的△ABC及其内部)，构造含待定量的任意函数，确定待定量的取值范围.

3 三元变二元，关键齐次式

二元线性规划的关键词之一是“二元”，一般地，齐次式通过“同除”可以减元，因此在命题实践中，有时呈现的约束条件是三元，但一定是齐次式形式，求解时必须“同除”以实现减元.

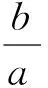
分析由已知及构成三角形的条件，得

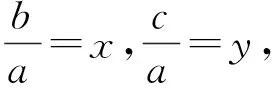
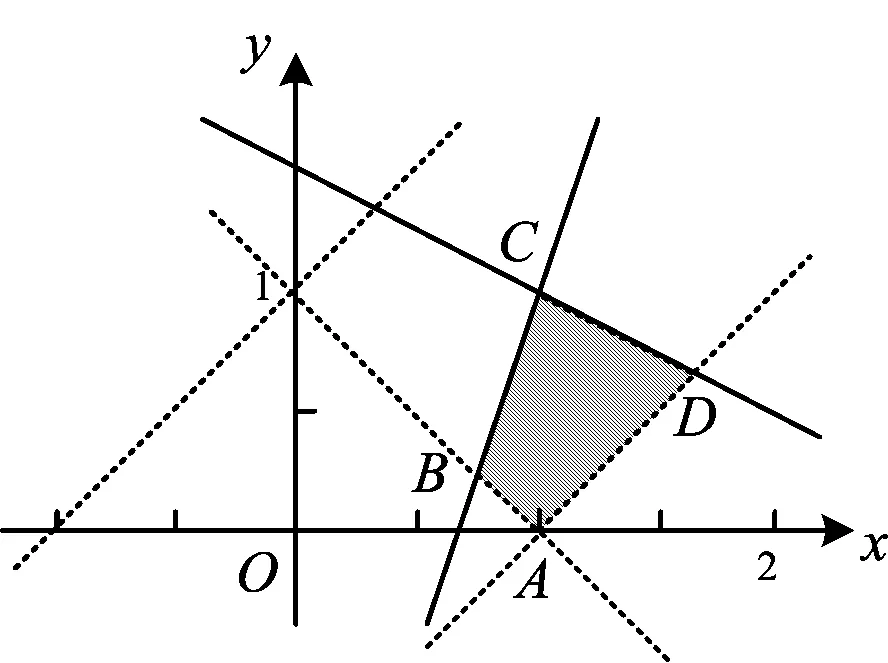
图3

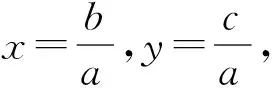
4 一次变二次，思想不会变

约束条件是线性的，也就是说，可行域的边界是直线型的.显然，也可以将可行域的边界改成曲线，即约束条件之一是二元二次不等式.

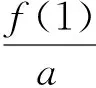
分析因为a>0，所以函数f(x)的图像是开口向上的抛物线.又f(x)在区间[1，2]上有两个不同的零点，从而

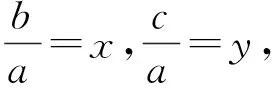
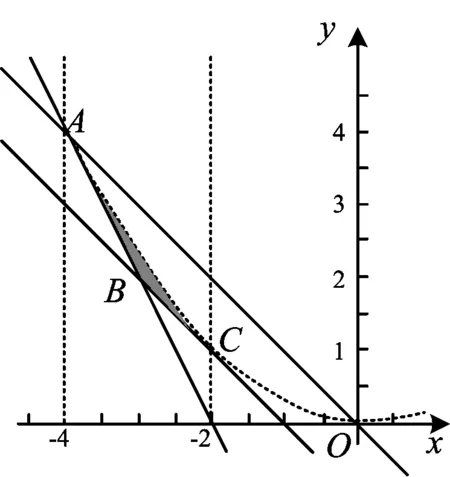
图4

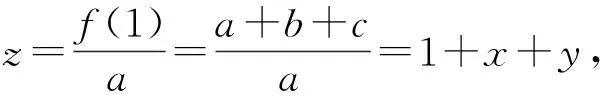
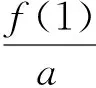
评注将约束条件用“一元二次方程根的分布”背景包装，其中的每一个不等式都是齐次式，目标函数也是齐次式，因此通过“同除”就可以将三元转化为二元规划问题，所不同的是，约束条件中有一个是二次的，即x2-4y>0，不难理解其表示的区域——抛物线x2-4y=0开口外的部分(不含边界).类似地，可以设计圆内(外)、椭圆内(外)，双曲线开口内(外)等二次约束条件.解题过程中要注意两点：一是考虑定义域；二是不要过分人为地复杂化.

5 数形结合好，万变不离宗

先画好一个曲边三角形(为控制难度，仅有一边是曲线)，拟定一条过定点(如原点)的动直线，求动直线斜率的取值范围.问题拟好后，再适当代换成三元问题，并改变个别约束条件的运算形式.下面的高考真题是否就是这样编拟的呢？

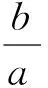
(2012年江苏省数学高考试题第14 题)

分析由5c-3a≤b≤4c-a及c>0，得

(1)

由clnb≥a+clnc得

(2)

于是式(1)即为 5-3x≤y≤4-x,

(3)

式(2)即为y≥ex.

(4)

图5

y-ex0=ex0(x-x0),

万变不离其宗，多变量不等关系约束下求(非)线性目标函数的取值范围，数形结合思想不变.从命题的角度看，一般先有图，将需要考查的想法融于图中；然后编拟二元规划问题，进行字母代换或运算代换后变为三元、非线性的问题；最后给约束条件和目标函数赋予恰当、新颖的背景.遵循这样的命题思路，读者也可以命制更多形式新颖、思路灵活、更有难度的试题.