改进循环维纳滤波器算法的滚动轴承复合故障诊断
郝 芳,王宏超
(1.黄河科技学院 民族学院,郑州 450063; 2.郑州轻工业学院 机电工程学院,郑州 450002)
随着旋转机械的大型化、高速化及结构复杂化,作为旋转机械中的关键零部件——滚动轴承,其故障信号也越来越复杂.传统的信号处理方法如快速傅里叶变换、包络解调方法等不能再有效提取出其故障特征.新的滚动轴承故障诊断方法如小波变换[1]、品质因子可调小波变换[2]、总体经验模态分解[3]、谱峭度[4]及改进快速Kurtogram[5]等相继出现,这些方法仅对滚动轴承单一故障或微弱故障[6]有效.现有滚动轴承复合故障诊断方法大多基于智能分类算法如隐马尔科夫及支持向量机等[7-11].这种方法具有计算量大、效率低、难以实现滚动轴承复合故障的及时诊断等缺点.基于信号处理的滚动轴承复合故障诊断方法十分有限.文献[12]提出了一种基于自适应冗余提升多小波的旋转机械复合故障诊断方法,而且验证了所述方法相对于其他方法的优势.文献[13]将双树复小波变换用于旋转机械的复合故障诊断.文献[14]将谱峭度方法加以改进,提出了一种自适应谱峭度算法,并将其用于多瞬态故障冲击成分的诊断,验证了改进方法相对于Protrugram[15]的优势.
本文将传统循环维纳滤波方法加以改进,提出基于改进循环维纳滤波的滚动轴承复合故障诊断.通过仿真及实验验证了所述方法的可行性、有效性及相对于传统循环维纳滤波器的优点.
1 循环维纳滤波器及改进方法
循环维纳滤波器是基于循环平稳信号谱相干理论提出的,有必要对谱相干基础理论作以简要叙述.
1.1 谱相干理论
(1)
式中:α,f分别为循环频率及谱频率.

(2)
式中:〈·〉为时间平均因子,
(3)
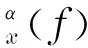
(4)
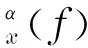
(5)
1.2 循环维纳滤波及改进方法
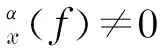

图1 循环维纳滤波示意图Fig.1 The sketch map of cyclic wigner filter
上述循环维纳滤波器以观测信号本身作为期望输出,对于滚动轴承单一故障诊断有效[16].当滚动轴承发生故障时,其观测信号为复合故障信号,传统维纳滤波器不再适用.期望输出作为循环维纳滤波器的参考信号,仅包含滚动轴承单一故障时的信号特征为最理想的情况.将图1所示的循环维纳滤波器加以改进,将滚动轴承单一故障的仿真信号分别作为循环维纳滤波器的期望输出d(n),改进后的循环维纳滤波器示意图如图2所示.
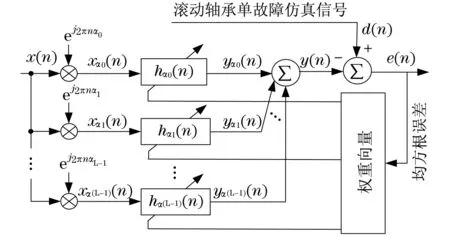
图2 改进循环维纳滤波器示意图Fig.2 The sketch map of improved cyclic wigner filter
2 仿真
用式(6)所示的滚动轴承单一故障数学模型[17]模拟滚动轴承的内、外圈故障.图3(a)为滚动轴承外圈故障,图3(b)为滚动轴承内圈故障,图3(c)为随机噪声,图3(d)为图3(a)~图3(c)所示信号的合成信号,用于模拟滚动轴承复合故障.设定采样频率fs=16 384 Hz,转频fr=12 Hz,外圈故障通过频率fo=57 Hz,内圈故障通过频率fi=103 Hz,τi为滚动体相对于滚道的微小随机滑动,假定其服从正态分布,标准差为转速的0.5%.
(6)
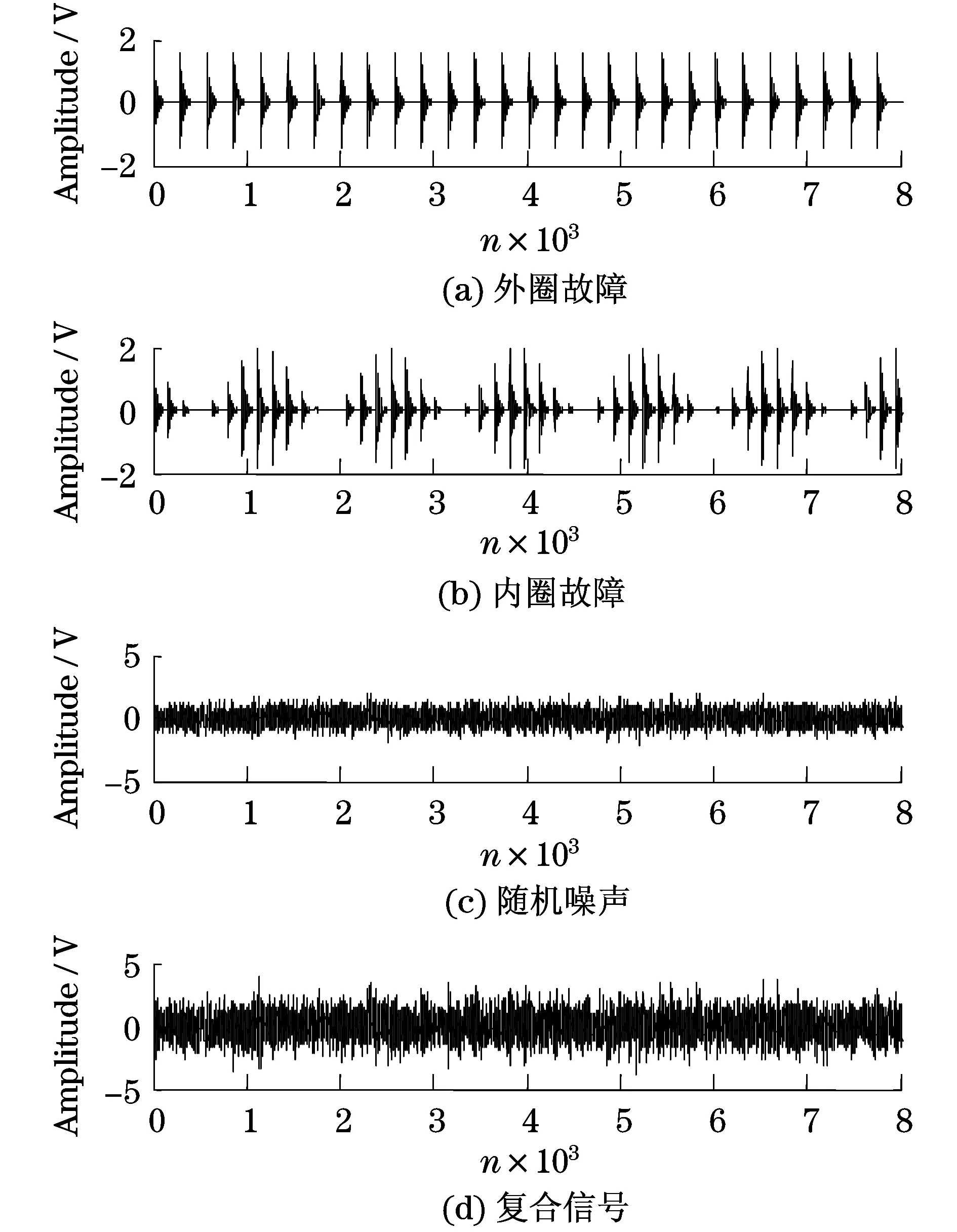
图3 滚动轴承复合故障仿真Fig.3 The simulation of bearing’ compound fault
图3(d)所示信号相对应的包络解调谱如图4所示,从中虽然可以提取出滚动轴承外圈故障特征频率的基频,但不能提取出其谐频,此外无法得到滚动轴承内圈故障的任何信息.
图5为所述方法的分析结果,其中:图5(a)是将图3(a)所示信号作为循环维纳滤波器的期望输出、图3(d)所示信号的循环维纳滤波结果;图5(b)是图5(a)所示信号的包络解调谱,从中可以看出外圈故障特征频率及其谐频被很好地提取出来;图5(c)是将图3(b)所示信号作为循环维纳滤波器的期望输出、图3(d)所示信号的循环维纳滤波结果;图5(d)是图5(c)所示信号的包络解调谱,从中可以看出内圈故障特征频率及其谐频被很好地提取出来,此外调制频率即转频也被很好地提取出来(注:滚动体相对于滚道的随机滑动τi造成了内、外圈实际提取故障特征频率与理论设定故障特征频率的误差).
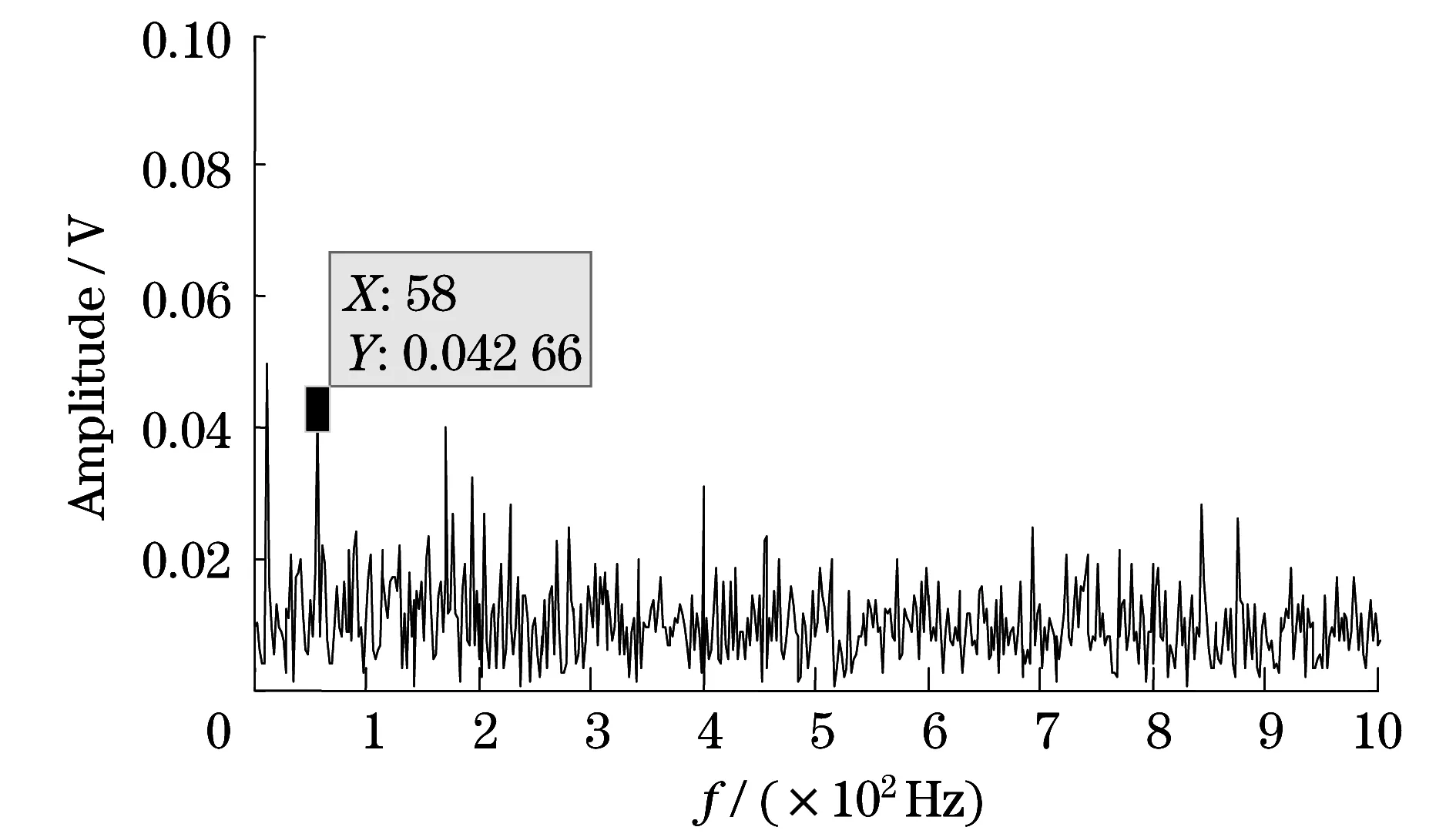
图4 图3(d)所示信号的包络解调谱Fig.4 The envelope demodulation spectral of the signal shown inFig.3(d)

图5 基于所述方法滚动轴承复合故障仿真信号的分析结果Fig.5 The analysis results of the simulation signal shown in Fig.3(d) using the proposed method
3 实验
以UN205滚动轴承为实验轴承进行实验,试件相关参数如表1所示,实验台场景如图6所示.实验过程中,轴承内圈随主轴旋转,外圈固定.通过线切割加工轴承内圈外圈及滚动体故障,故障如图7所示.根据表1相关参数及式(7)~式(9)滚动轴承故障特征频率计算公式得到试件的外圈、内圈及滚动体故障特征频率分别为:fo=64.41 Hz,fi=95.38 Hz,fb=5.38 Hz.根据3种计算故障特征频率及式(6)构建循环维纳滤波器的3种期望输出信号(外圈、内圈及滚动体)分别如图8(a)~图8(c)所示.

表1 试件轴承相关参数Tab.1 The parameters of the test bearing

图6 实验台实景图Fig.6 The test rig

图7 试件故障Fig.7 The fault of the test bearing

图8 所述方法构建的期望输出信号Fig.8 The constructed ideal output signals using the proposed method
复合故障信号的时域图及包络解调谱如图9(a)和图9(b)所示.由图9(b)所示,仅仅可以得到内圈故障特征基本频率,无法得到外圈及滚动体故障的任何特征信息.图10是所述方法的分析结果.图10(a)是用图8(a)所示信号作为期望输出、图9(a)所示信号的循环维纳滤波结果、图10(a)是相应的包络解调结果,从中外圈故障特征频率及其谐频被很好地提取出来;图10(c)是用图8(c)所示信号作为期望输出、图9(a)所示信号的循环维纳滤波结果、图10(d)是相应的包络解调结果,从中滚动体故障特征频率及其谐频被很好地提取出来;图10(e)是用图8(b)所示信号作为期望输出、图9(a)所示信号的循环维纳滤波结果、图10(f)是相应的包络解调结果,从中内圈故障特征频率及其谐频不仅被很好地提取出来,而且滚动轴承发生内圈故障时的调制频率即转频也被很好地提取出来.
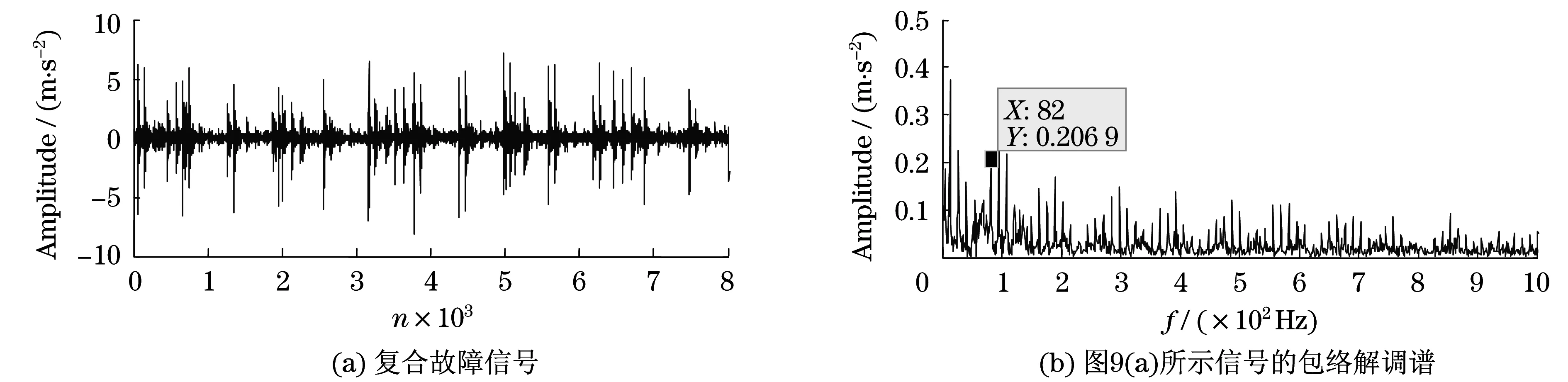
图9 复合故障实际实验信号Fig.9 The experiment compound fault signal
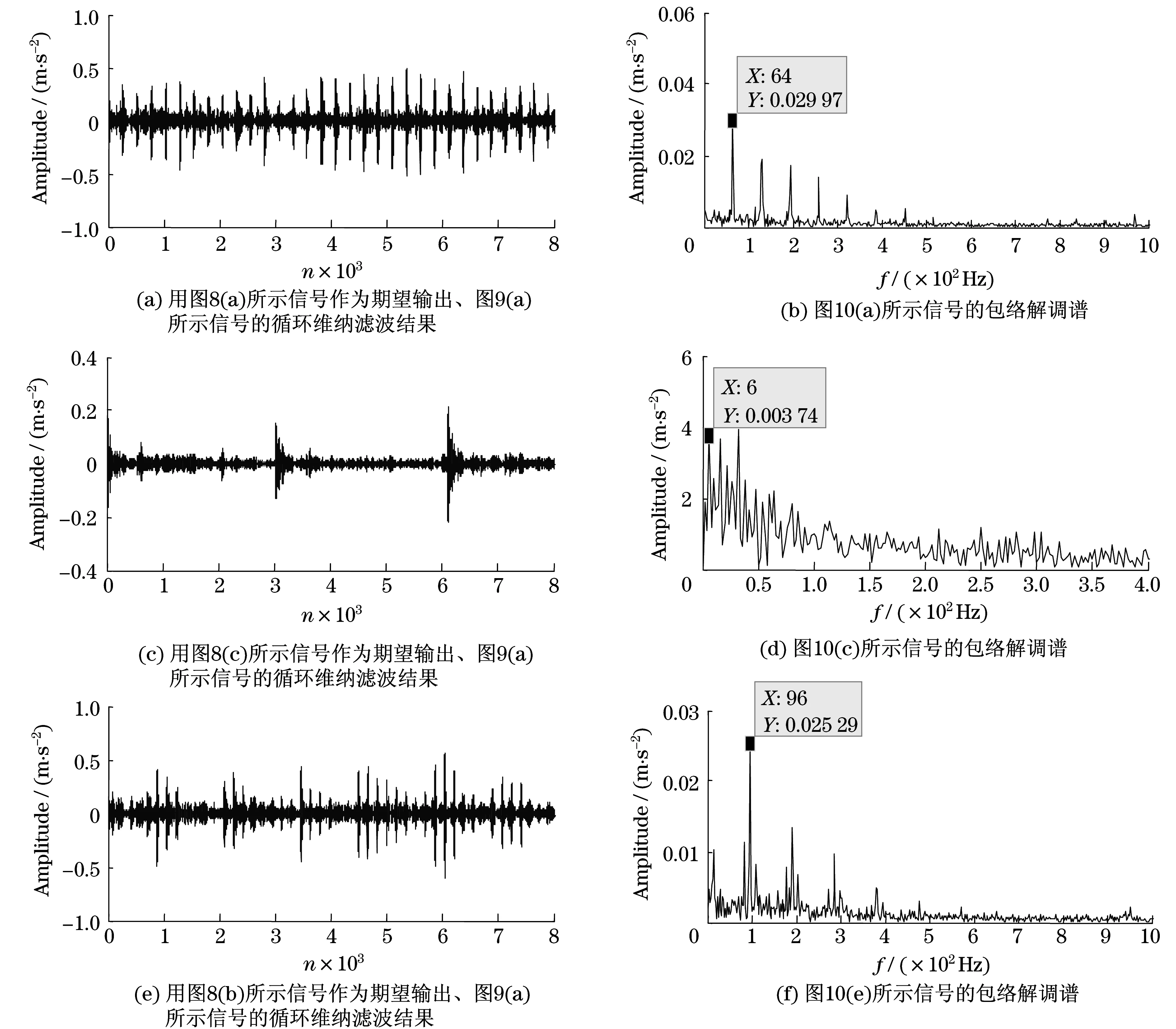
图10 基于所述方法复合故障实验信号的分析结果Fig.10 The analysis result of the experiment compound signal using the proposed method
4 结论
本文对传统循环维纳滤波器加以改进并将其用于滚动轴承的复合故障诊断,通过仿真验证了所述方法的可行性.再通过滚动轴承实际复合故障实验信号,验证了所述方法在滚动轴承复合故障诊断中的有效性.同时,验证了所述方法相对于传统循环维纳滤波器在滚动轴承复合故障诊断中的优势.

