偏心量影响下的裂纹转子非线性研究

刘桂珍,于 影,龚伟胜,崔博林,田鑫磊,闻邦椿

(1.佳木斯大学 机械工程学院,黑龙江 佳木斯 154007; 2.东北大学 机械工程与自动化学院,沈阳 110819)

裂纹故障是旋转机械最常见的故障之一.伴随大型旋转机械向高速化发展,转子系统作为其重要部件出现裂纹故障的频率不断增大.裂纹导致转轴刚度减小并发生周期性变化,影响转子运行的稳定性.作为转子系统后果最严重、最难以及时发现的故障,一旦裂纹扩展到一定程度后,就会引发突发性的事故,造成巨大的损失[1-3].所以，研究大型旋转机械裂纹转子的动力特性,提取转子裂纹故障的特征信息，对设备安全预防具有重要的工程意义[4].

本文以裂纹故障为研究对象,利用拉格朗日方程建立了非稳态油膜力作用下裂纹转子系统故障的4质量8自由度动力学模型,应用数值分析法,研究了当偏心量变化作为唯一控制参数时,裂纹转子系统的动态响应.通过提取该故障转子的分岔图、时域波形图、幅值谱图和Poincare截面等振动信号的故障信息,对该系统响应的非线性行为和故障机理进行分析,所研究结果为大型旋转机械的故障诊断和系统的安全运行提供理论依据.

1 力学模型与微分方程

1.1 拉格朗日方程描述

设有n个质点组成的质点系,受完整理想约束,具有N个自由度,其位置可由N个广义坐标方程来确定,则有

(1)

式中:T系统的动能函数;Qi为作用在系统上的广义力;qi为系统独立的广义坐标;N为系统的总自由度个数.

1.2 刚度影响系数的计算

设转轴半径为R、长度为L1的无质量弹性圆轴,在转轴中央有一深度为a的弓形横向裂纹,如图1所示.如果只考虑裂纹处弯矩的作用,根据断裂力学理论,由于裂纹的存在将在裂纹局部产生附加角位移.设在η,ξ方向弯矩作用下的局部柔度系数分别为[5-6]

(2)

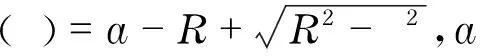
0.199[1-sin(πη)]4}/cos(πη/2h)

2.02(η/h)+0.37[1-sin(πη)]3}/

cos(πη/2h)

(3)

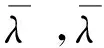
(4)

式中:LR为支承跨度与转盘位置的无量纲系数;v为泊松比.

1.3 非稳态油膜力模型[7]

非线性油膜力模型采用短轴承假设下的Ca-pone非线性油膜力模型,该模型有较好的精度和收敛性.在短轴承油膜力假设条件下的无量纲雷诺方程为

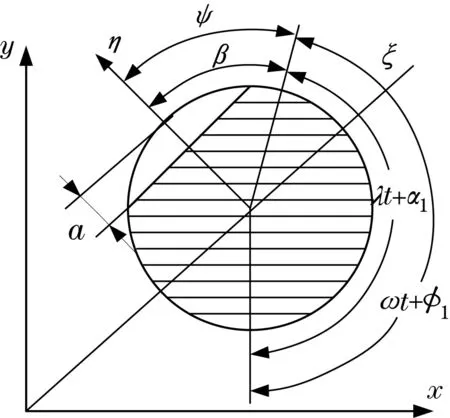
图1 裂纹截面示意图Fig.1 Crack section of the rotor

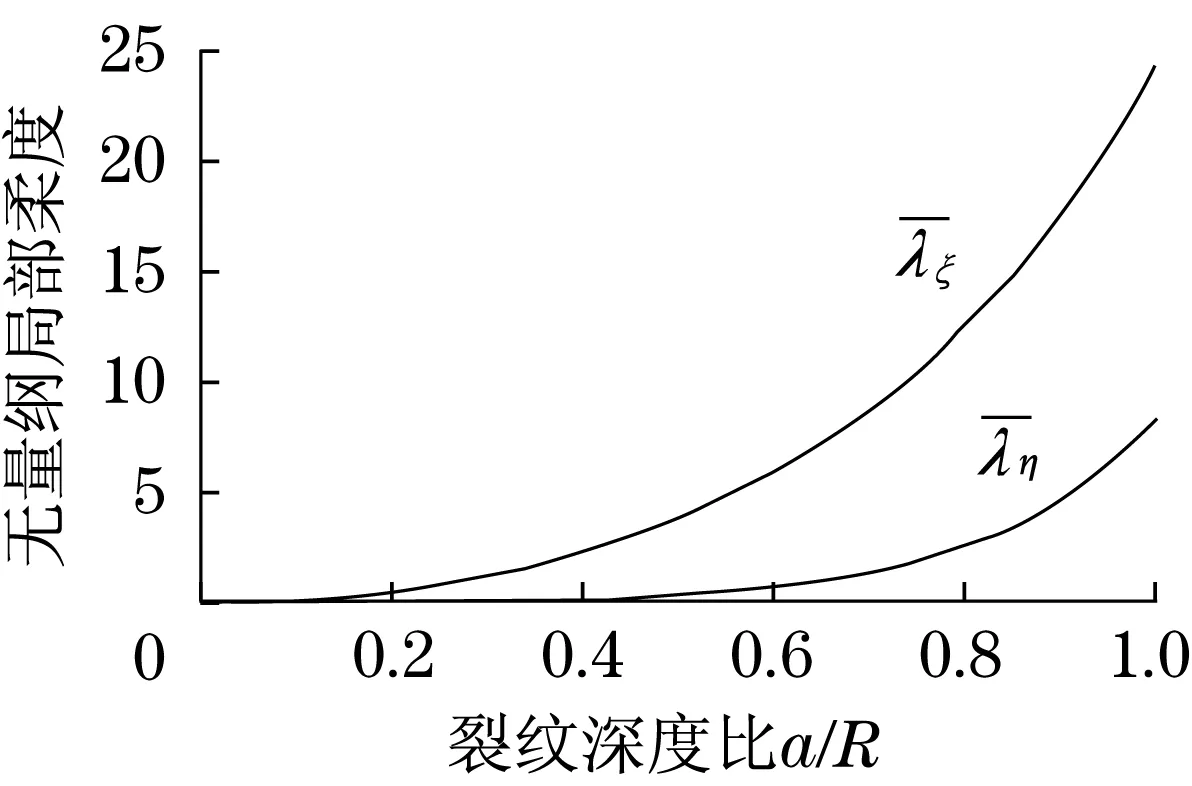
图2 柔度与无量纲裂纹深度关系Fig.2 Relation between flexibility and the crack deepness

(5)

由式(5)可得无量纲油膜压力为

(6)

式中:D为轴承直径.

无量纲非线性油膜力最终可以表示为

(7)

式中:

1.4 运动微分方程

图3所示为转子-定子-轴承系统中间轴上具有一横向裂纹的力学模型,两端由滑动轴承支撑,两轴承之间为一无质量弹性转轴,其转轴半径为R,长度为L1,转轴中央有一对称布置的圆盘,以及深度为a的弓形横向裂纹.O1为转子的几何中心;Oc为转子质心;mi(i=1,2,3,4)分别为转子、轴承、定子和转轴在轴承处的半集中质量,kg;ki(i=1,2,3)分别为转轴、轴承支撑处和定子基础的刚度系数,N·m-1;ci(i=1,2,3)分别为转轴、轴承支撑设转盘在水平方向、垂直方向移动的位移为x1,y1，左端轴承在水平方向、垂直方向移动的位移为x2,y2，定子在水平方向、垂直方向移动的位移为x3,y3，右端轴承座处水平方向、垂直方向移动位移x4,y4.

处和基础对定子的阻尼系数,N·sm-1.

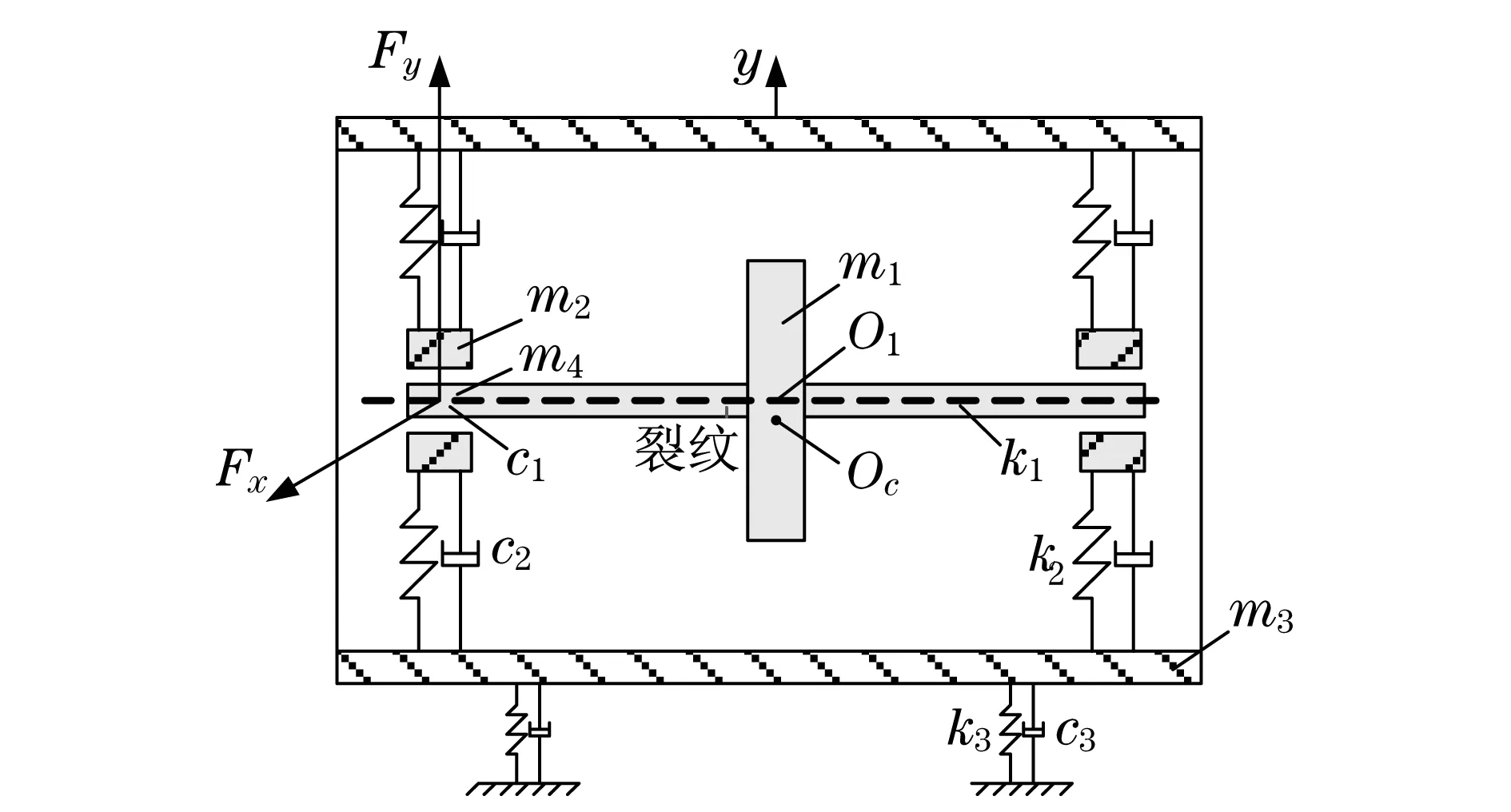
图3 裂纹故障力学模型Fig.3 Mechanical model of crack fault

采用耗散能量形式的拉格朗日方程推导出对应裂纹故障的转子-定子-轴承系统的质点运动微分方程:

(8)

式中:xi,yi(i=1,2,3,4)分别为应各质量的位移坐标;e为轴颈偏心量,b为圆盘偏心量,mm;Fx,Fy分别为水平、铅垂方向的油膜力,N.

2 数值模拟

运用四阶Runge-Kutta法对数值进行求解.在计算中为了能够较快地得到稳定解,应将步长选得尽量小且周期足够多.为了消除瞬态响应的影响,舍弃前40个周期,计算轨迹图时取后10～20个周期.选取系统参数如下:m1=4.0 kg,m2=32.1 kg,m3=50.0 kg,m4=20.0 kg;c1=1.05 kN·sm-1,c2=2.1 kN·sm-1,c3=2.1 kN·sm-1;k1=250 kN ·m-1,k2=250 kN·m-1,k3=25 000 kN·m-1,kr=1 000 kN·m-1;R=0.025 m;L=0.570 m;δ2=0.2 mm;η=0.018 MPa;R1=0.015 m;f=0.2;通过计算得出转子系统的三级固有频率分别为f1=13.974 7 Hz,f2=43.586 4 Hz,f3=113.109 6 Hz.

图4(a)和图4(b)分别表示转子系统在激励频率ω=420 rad/s、裂纹初始相角β=π/2时转子系统响应随圆盘偏心量b变化的x,y方向变化的分岔图.

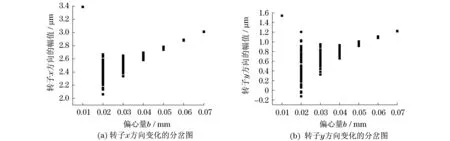
图4 系统响应x，y随圆盘偏心量b变化的分岔图Fig.4 System response of x and y with the bifurcation diagram of the disc eccentricity b changing

图4中:当b=0.01 mm时,系统响应为周期运动;当b在区间(0.02,0.04)mm时,系统经周期运动演变为混沌运动;当b在区间(0.05,0.06)mm时,系统响应为拟周期运动;当b在(0.06,0.07)mm时,系统响应为周期运动.由图4可知,偏心量的大小对转子系统的动力学行为有较大的影响.

图5～图8是激励频率ω=420 rad/s、裂纹初始相角β=π/2时,对应不同偏心量变化时的转子系统响应.

当偏心量b=0.01 mm时,Poincare截面为一孤立点.幅值谱图中在1/4倍频、3/4倍频和5/4倍频等处出现离散谱峰;当偏心量b=0.02～0.04 mm时,Poincare截面为散点图状态.幅值谱图中在2/3倍频、近1倍频、近2倍频以及近3倍频等处出现离散谱峰;当偏心量b=0.05～0.06 mm时,Poincare截面有周期吸引子,幅值谱图中在1/4倍频、1倍频和7/4倍频等处出现离散谱峰;当偏心量b=0.07 mm时,Poincare截面呈一孤立点.幅值谱图中在1/3倍频、1/2倍频、2/3倍频等处出现离散谱峰.其动态响应如图5～图8所示.

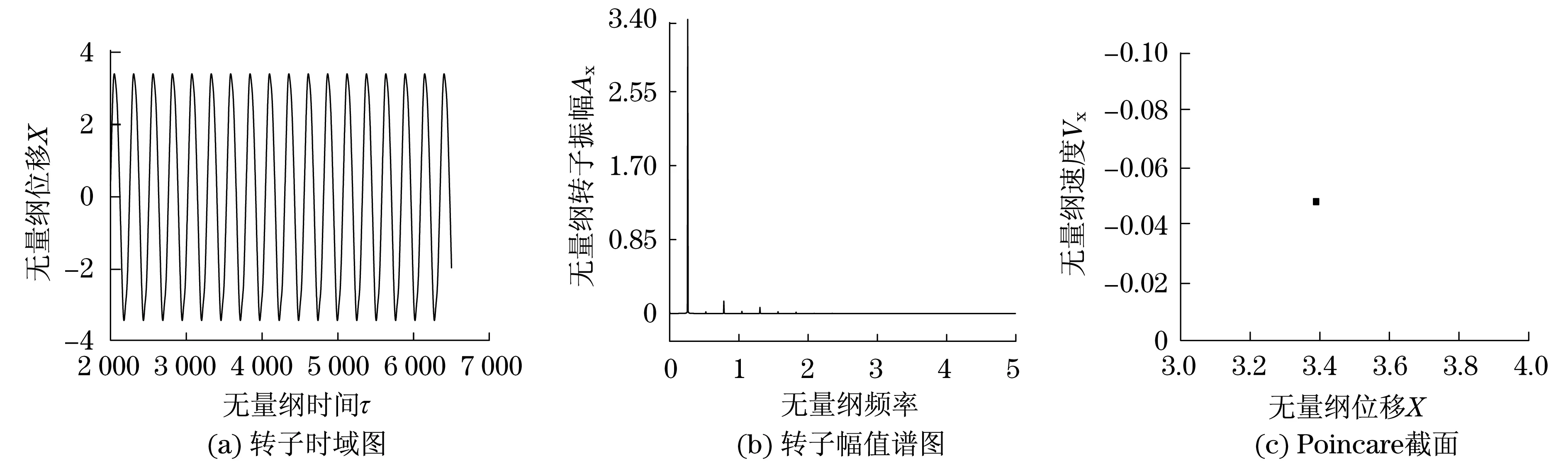
图5 b=0.01 mm时转子系统响应的时域图、幅值谱图和Poincare截面Fig.5 Time-domain graph, frequency spectrum and Poincare map when b=0.01 mm

图6 b=0.04 mm时转子系统响应的时域图、幅值谱图和Poincare截面Fig.6 Time-domain graph, frequency spectrum and Poincare map when b=0.04 mm

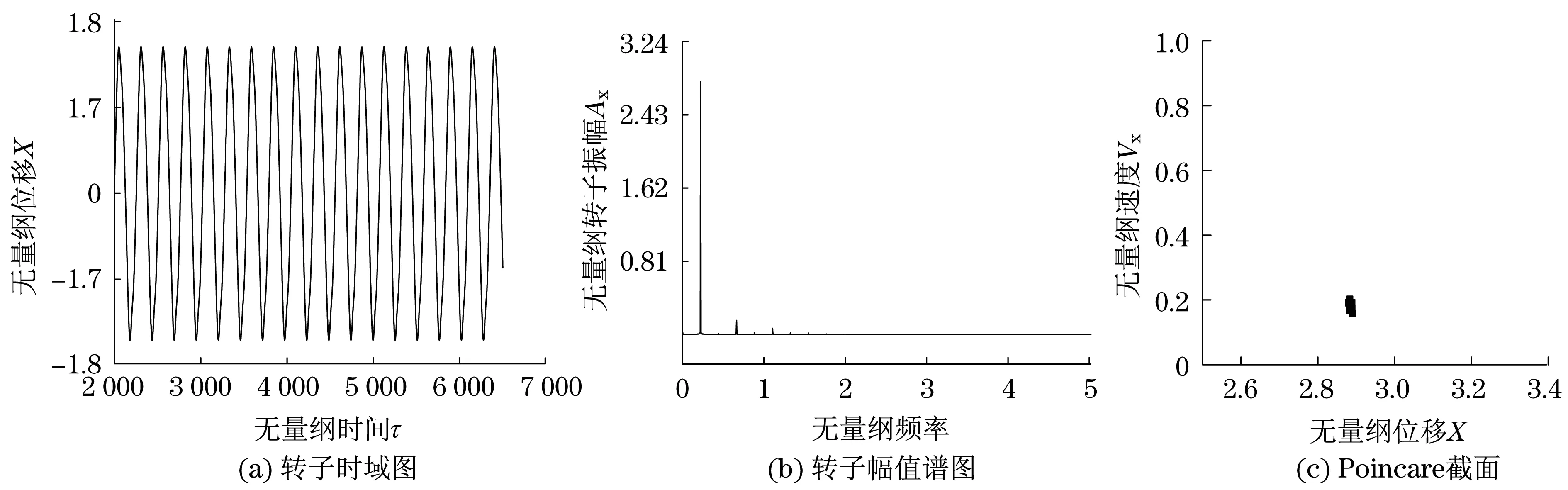
图7 b=0.06 mm时转子系统响应的时域图、幅值谱图和Poincare截面Fig.7 Time-domain graph, frequency spectrum and Poincare map when b=0.06 mm

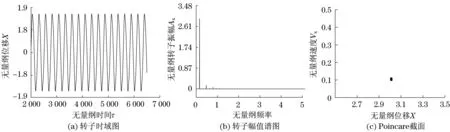
图8 b=0.07 mm时转子系统响应的时域图、幅值谱图和Poincare截面Fig.8 Time-domain graph, frequency spectrum and Poincare map when b=0.07 mm

3 结论

对带有裂纹故障转子-定子-轴承系统在不同偏心量下的运动特性研究,得出以下结论:

(1) 偏心量大小对运动的影响主要体现在分岔和混沌的时间上,当偏心量参数达到某一值时,系统响应不经过一系列分岔,而是突然变为非周期混沌运动,系统非线性变化的特点是分岔过程具有明显的跳变现象;

(2) 裂纹的存在使转轴刚度发生周期性变化,从而使转子系统产生低频激振现象;

(3) 随着转子偏心量的不同,系统周期运动的稳定性表现为上下波动,在一定偏心量的作用下转子系统表现出较强的稳定性.