改进粒子群算法的蒸汽喷射器结构优化
王小娇,李 阳
内蒙古工业大学 土木工程学院,呼和浩特 010051)
喷射式制冷系统以消耗高压蒸汽为代价,利用其通过拉法尔喷嘴加速后产生的低压真空区,卷吸低压制冷蒸汽并进行混合升压,从而代替传统压缩机进行制冷循环.喷射式制冷可以充分利用余热、废热等低品位热源,避免传统压缩机的机械能损耗,其原理简单,易于工程实现,是一种节能环保的制冷方式[1-2].蒸汽喷射器是喷射式制冷系统的核心部件.因此,提高喷射器的工作性能,对喷射式制冷系统来讲至关重要.
蒸汽喷射器主要由(拉法尔)喷嘴、卷吸室、混合室、扩压室4部分组成(见图1),这4个部分的结构尺寸对蒸汽喷射器的整体工作效率影响非常明显.因此,如何使这4个部分的结构尺寸达到最优匹配是十分必要的.在蒸汽喷射器的结构优化分析中,多数学者通常采用单因素敏感度分析法[3-7],但该方法忽略了多个参数同时变化时的相互制约性对喷射器工作性能的影响,如对其所有的结构参数进行全面试验,工作量巨大,时间成本将难以实现.
本文首先对初步设计的蒸汽喷射器结构参数进行单因素敏感度分析,在此基础上,利用二次回归正交组合设计方法,建立喷射器结构参数对喷射系数的回归方程;然后选用粒子群算法(Particle Swarm Optimization,PSO)和一种改进的粒子群算法(Genetic Algorithm Particle Swarm Optimization,GA-PSO)对回归方程在解空间内进行迭代寻优,并与单因素敏感度分析的结果对比,得到设计工况下蒸汽喷射器的最优结构参数组合.
1 模型建立与CFD数值模拟
1.1 蒸汽喷射器结构设计
引射蒸汽的质量流量与工作蒸汽的质量流量的比值称为喷射系数μ,是表征蒸汽喷射器工作性能的重要指标.本文以提供5 kW制冷量的蒸汽喷射制冷系统为应用背景.设计工况下,系统发生温度Tm=368 K,蒸发温度Te=280 K,冷凝温度为Tg=310 K,选用制冷剂R134a作为系统流动工质,忽略工质在管道及设备内的流动损失.初步设计的结构尺寸如表1所示,蒸汽喷射器模型如图1所示.
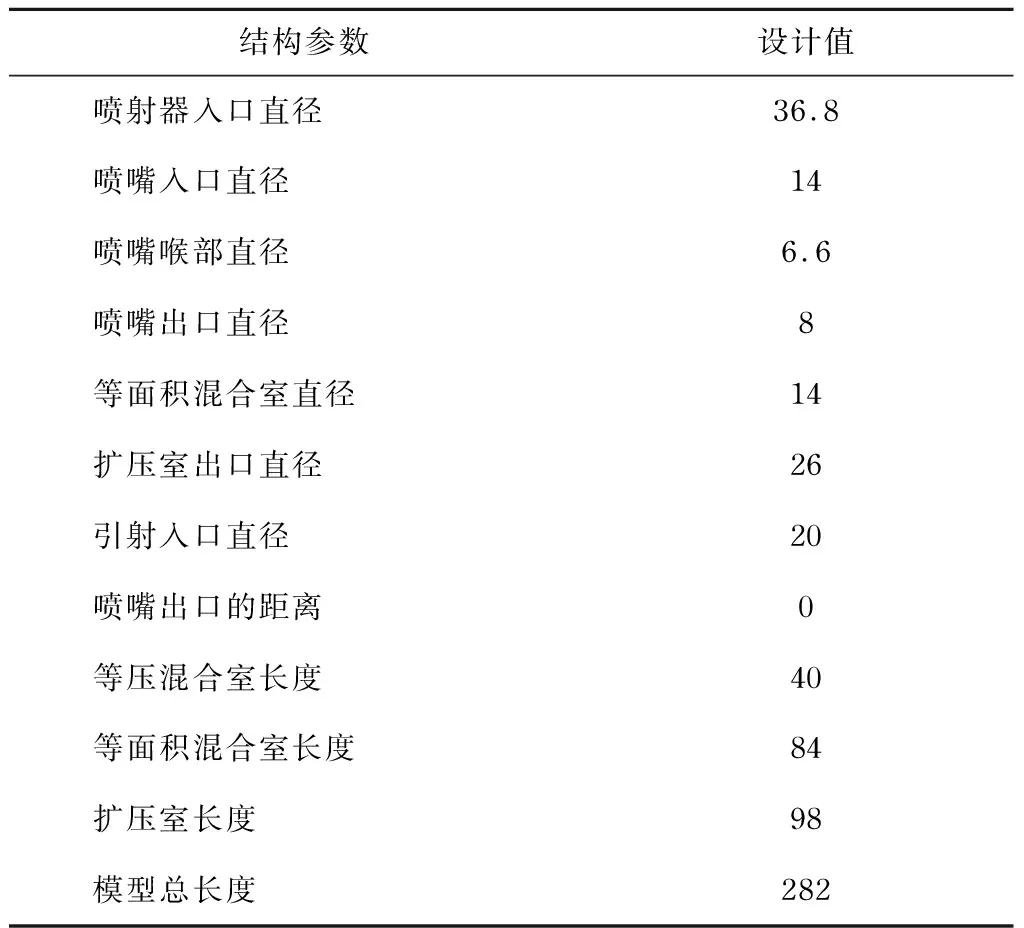
表1 蒸汽喷射器结构参数Tab.1 Steam injector structural parameters mm
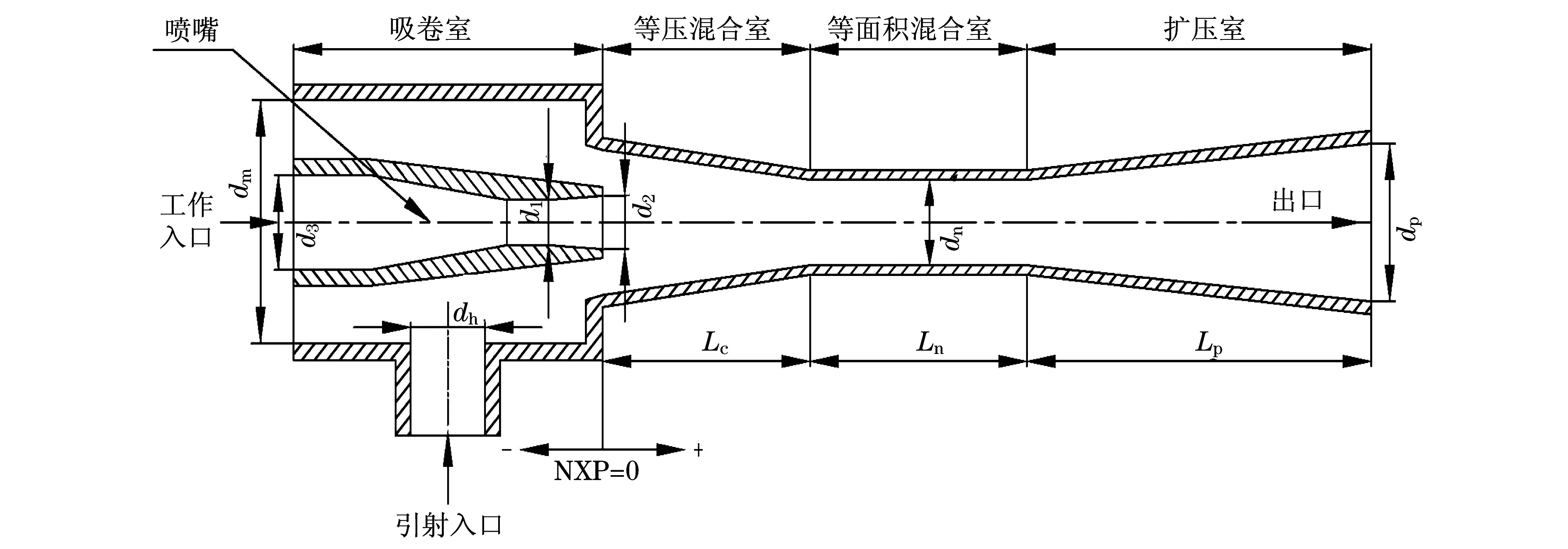
图1 蒸汽喷射器模型Fig.1 Steam injector model
1.2 CFD数值模拟
工作介质在喷射器内部流动时满足质量守恒方程、动量守恒方程和能量守恒方程,具体如下:

(1)
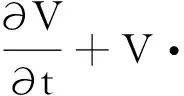
(2)
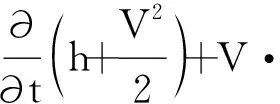
(3)
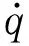
利用有限元处理软件Ansys 15.0平台下Geometry模块和Mesh模块,对喷射器进行计算模型的建立和网格划分.喷射器的网格划分采用自适应性更强的四面体非结构化网格,并在喷嘴喉部和喷嘴出口处流场变化梯度比较大的区域进行网格加密处理,网格数总计72 945个.在Fluent求解器中导入划分好网格的计算模型并进行求解设置:流体在喷射器内部为湍流可压缩流动,采用realizablek-ε湍流模型,近壁面采用增强壁面函数处理;喷射器进口、出口边界条件均设置为压力入口和压力出口,其余与流体接触的固体壁面采用无滑移边界条件与绝热边界条件;制冷剂R134a在喷射器内为等熵绝热流动,按理想饱和蒸汽处理,其密度为14.419 kg/m3,比热为883 J·kg-1·k-1,导热系数0.012 W·m-1·k-1,粘度系数为1.094×10-5kg·m-1·s-1;压力速度耦合方式选择Coupled,动量与湍动能方程采用二阶迎风格式离散.当各变量的迭代残差小于10-3且进出口的质量流量保持守恒时,认为计算收敛.
1.3 模型验证
为了保证本文试验数据的可靠性,参考Wang等[8]所用的实验蒸汽喷射器模型,将数值计算结果与实验结果进行对比.以R134a为制冷剂,当引射流体压力为Pe=0.4 MPa,出口背压为Pc=0.75 MPa时,喷射系数μ随工作流体压力Pm的变化情况如图2所示.
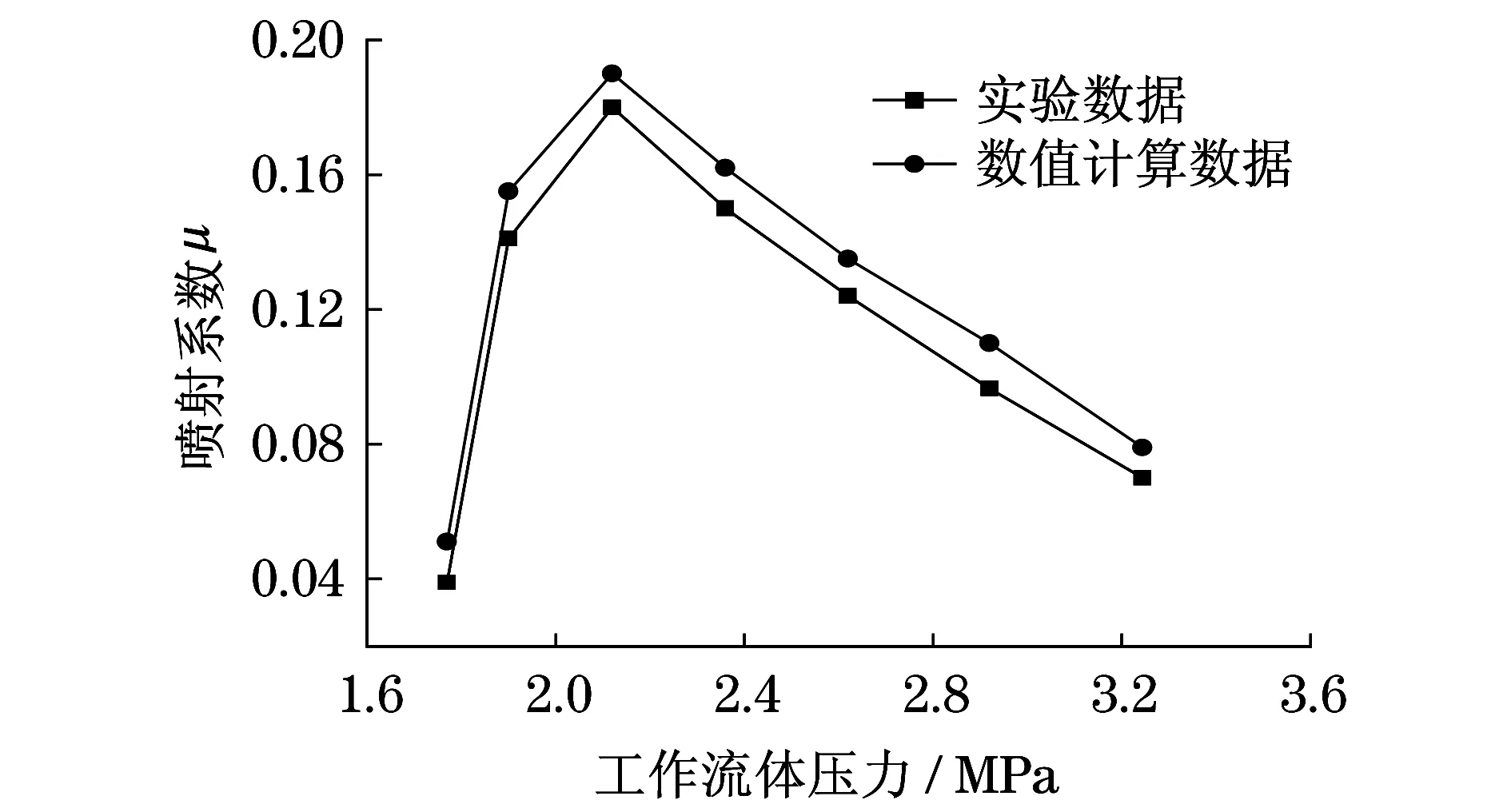
图2 实验数据与数值计算结果比较Fig.2 Comparison of experimental data with numerical results
从图2可以看出:工作流体压力Pm在1.6~3.25 MPa范围内增大时,喷射系数μ先增大后减小;在Pm=2.117 MPa时,μ达到最大值.通过对比发现,数值计算数据与实验数据基本一致,都能很好地描述Pm在一定范围增大时,μ的变化趋势.数值计算结果相对于实验结果略高是由于流体在喷射器内部流动时,产生的激波或相变使得能量损失增加,引射流量降低,而数值计算中选择特定的湍流模型,有些能量损失未考虑.因此,数值计算结果会比实验结果略高.
2 单因素敏感度分析
通过调研参考文献[3-7,9-11]得到:蒸汽喷射器的喷嘴喉部直径d1、等面积混合室直径dn、等面积混合室长度Ln、扩压室长度Lp和喷嘴出口的位置NXP对其工作性能的影响较为显著.因此,保持其他结构参数不变,研究单一结构参数的改变对喷射系数μ的影响规律,如图3所示.
图3表明:喷嘴喉部直径d1、等面积混合室直径dn、等面积混合室长度Ln、扩压室长度Lp在一定范围增加时,喷射系数μ先增大后减小;μ取最大值时所对应的取值为d1=6.8 mm,dn=14 mm,Ln=84 mm,Lp=112 mm;喷嘴出口的位置NXP在-2~20 mm范围内增大时,喷射系数μ先增大;当NXP达到8 mm之后,μ基本保持不变.
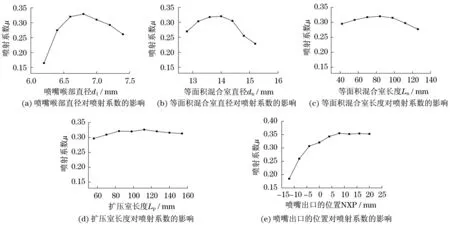
图3 结构参数对喷射系数的影响Fig.3 The influence of structural parameters on the jetting coefficient
3 改进的粒子群算法
3.1 二次回归正交组合设计
将d1,dn,Ln,Lp,NXP作为设计变量,分别记为x1,x2,x3,x4,x5,以喷射系数μ为设计指标.根据单因素敏感度分析结果,当喷射系数μ取得最大值,将对应的d1,dn,Ln,Lp和NXP的取值作为其编码后的零水平,并确定各试验因素上下限水平X1j,X1j和变化区间Δj∶Δj=(X1j+X2j)/γ,其中,γ为星号臂长度.查表可得γ=1.771,试验因素与水平如表2所示.
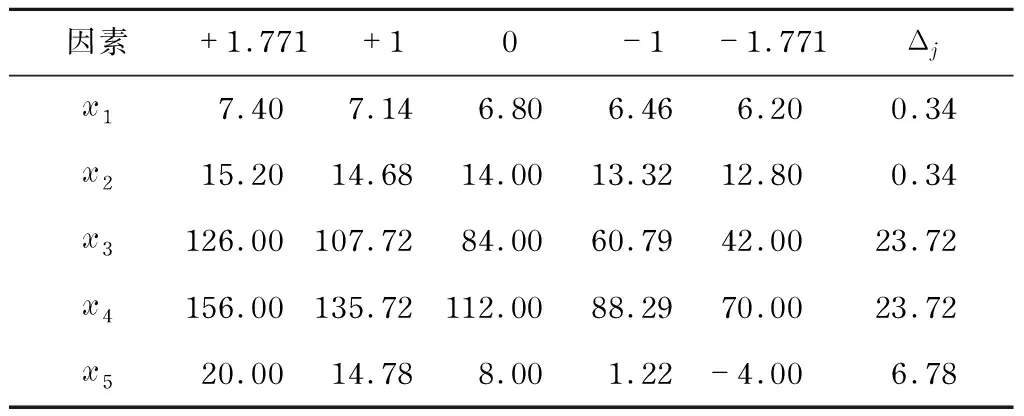
表2 设计因素及水平Tab.2 Design factors and levels mm
根据五元二次回归正交组合设计表(1/2实施试验,m0=5),对设计变量的不同水平进行二次回归正交组合设计,得到喷射系数μ的数值计算结果,如表3所示.
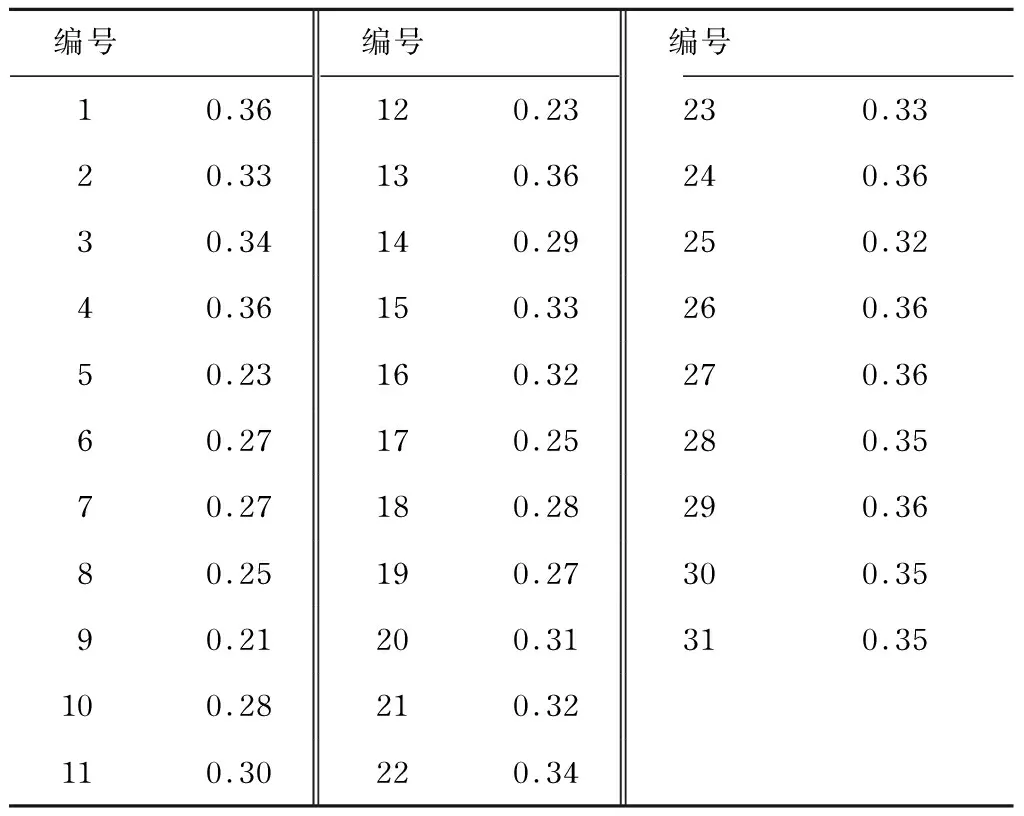
表3 数值计算结果Tab.3 Numerical results
对表3中的数值计算结果进行统计分析,得到各设计变量对喷射系数μ的回归方程:
(4)
3.2 标准粒子群算法
五元二次回归数学模型属于多维、非线性函数,利用传统的解析法很难得到精确的解析解.因此,需要一种高效可靠的算法来解决这类复杂函数的数学求解问题.群体智能算法是一种基于生物特征的启发式算法[12-13],包括蚁群算法[14]、遗传算法[15]、模拟退火算法[16]、粒子群算法[17]等.其中,PSO通过群体中个体间的信息共享与相互协作,能够实现在复杂的解空间中对最优解的搜索,尤其在解决多峰高维函数的优化问题时表现出非常强的优越性[18-21].
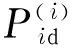
式中:i为粒子编号,1≤i≤m;w为惯性权重值,反映了粒子收敛速度在局部搜索和全局搜索之间的选择;c1,c2为学习因子;r1和r2为均匀分布于[0,1]之间的随机数.
3.3 改进粒子群算法
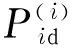
步骤1基本参数设置:种群规模n;最大迭代次数itermax;种群粒子的速度边界值[Vmin,Vmax];学习因子c1和c2等.
步骤2参数初始化:初始迭代次数iter=0,随机初始化粒子的位置和速度,并计算每个粒子的适应度值.
步骤3将每个粒子的当前位置作为个体最优Pid,当前粒子中适应度最好的作为全局最优Pgd.
步骤4计算w值,并更新粒子的速度和位置.
步骤5对种群粒子按一定概率进行变异操作.
步骤6计算每个变异粒子的适应度值,获取个体最优Pid和全局最优Pgd.
步骤7iter=iter+1,若iter≥itermax,则输出全局最优值Pgd,算法结束;反之,继续进入步骤2迭代计算.
3.4 算法寻优
本文以d1,dn,Ln,Lp和NXP为蒸汽喷射器待优化结构参数,喷射系数μ为优化目标,回归方程式(4)为目标函数,将每个结构参数的优化范围作为目标函数的约束条件,对蒸汽喷射器进行结构参数优化设计.其中,d1的优化范围为[6.2,7.4] mm,dn的优化范围为[12.8,15.2] mm,Ln的优化范围为[42,126] mm,Lp的优化范围为[70,154] mm,NXP的优化范围为[-4,20] mm.
利用PSO和GA-PSO分别对喷射器上述数学模型进行Matlab迭代寻优.在相同的参数设置下,对PSO算法和GA-PSO算法的迭代计算结果进行比较.参数设置为:种群规模n=20,最大迭代次数iter=1 000,粒子运行速度边界[Vmin,Vmax]设为[-1,+1],学习因子c1=c2=2.在算法执行过程中,将喷射系数μ作为喷射器结构参数优化的适应度函数.惯性权重w设置为随GA-PSO迭代次数递减的线性函数,使算法初期具有较强的全局搜素能力.随着迭代计算的进行,算法后期的局部搜索能力逐渐增强,算法的整体性能得以提高,具体公式如下:
(7)
喷射系数根据PSO和GA-PSO的迭代计算,结果如图4所示.由图4可知,PSO和GA-PSO在迭代寻优过程中,GA-PSO具有较快的收敛速度和较好的优化结果.这是由于GA-PSO中加入随机变异,增强了算法的全局搜素能力,得到的优化结果更符合寻优要求.
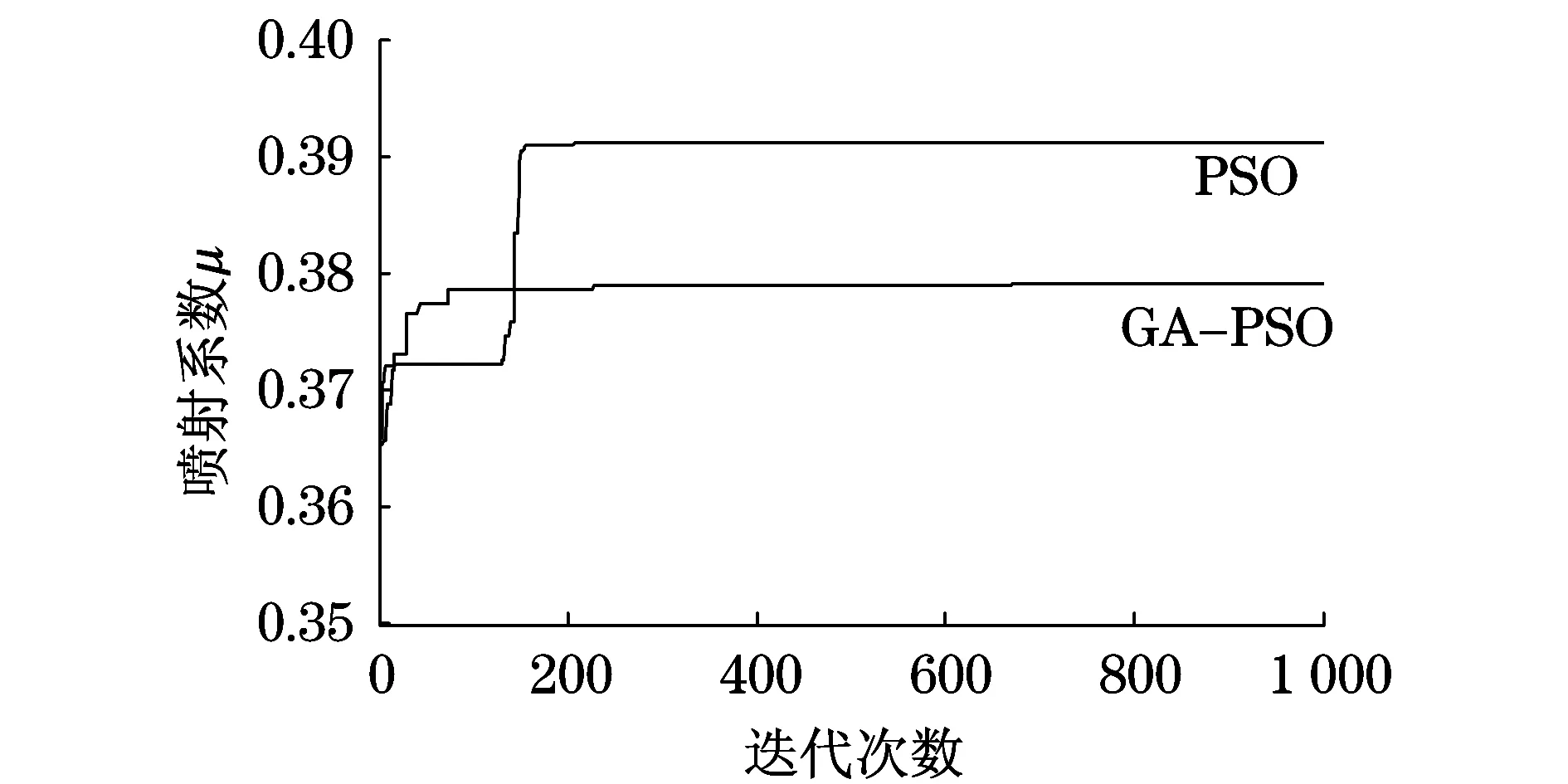
图4 PSO和GA-PSO寻优曲线Fig.4 PSO algorithm and GA-PSO algorithm optimization curve
将单因素敏感度分析法、基于二次回归正交设计的PSO和GA-PSO得到的喷射器结构参数优化结果与初步设计的喷射器结构参数进行对比,如表4所示.
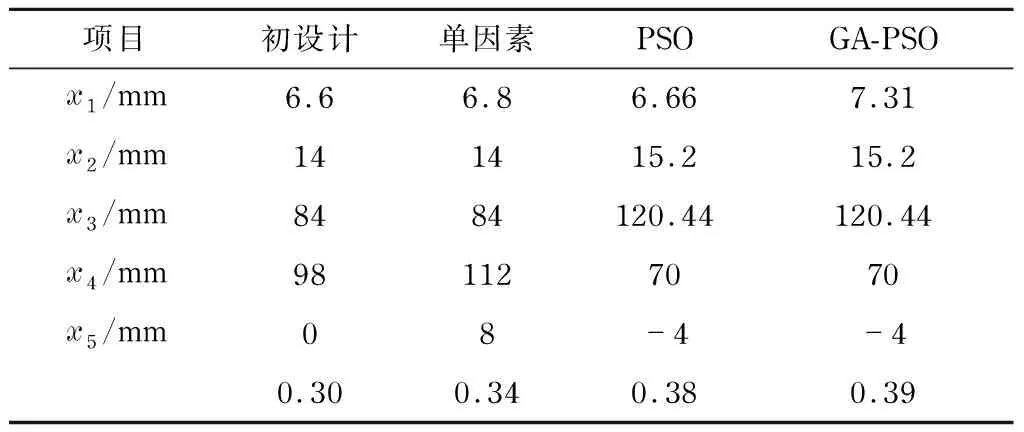
表4 喷射器结构参数优化Tab.4 Injector structure parameters optimization
从表4可以看出:在蒸汽喷射制冷系统运行工况和系统工质的热力学参数不变的前提下,单因素敏感度分析法、基于二次回归正交设计的PSO和GA-PSO都取得了良好的优化效果,但得到的喷射器结构参数优化组合存在一定差异;PSO和GA-PSO得到的喷射器结构参数优化结果明显优于单因素敏感度分析法;GA-PSO比PSO对喷射器结构参数优化后的喷射系数μ提高了2.6%.
在进行喷射器结构参数单因素敏感度分析时,忽略了多个结构参数同时变化对喷射系数μ的影响.二次回归正交组合设计考虑到各结构参数变化之间的相互制约性,建立起喷射器结构参数对喷射系数μ的回归方程,并在约束条件范围内,利用PSO和GA-PSO对回归方程进行迭代寻优.GA-PSO由于变异因子的引入使得种群全局搜索能力增强.因此,GA-PSO比PSO得到的优化效果更好.
4 结论
基于二次回归正交组合设计的GA-PSO比单因素敏感度分析法得到的喷射系数μ提高了0.05,PSO比单因素敏感度分析法优化得到的喷射系数μ提高了0.04.因此,GA-PSO比PSO的优化效果更好,优化得到的喷射系数μ提高了2.6%.在工作参数不变的情况下,GA-PSO对蒸汽喷射器进行优化后的的最佳结构参数组合:d1=7.31 mm,dn=15.2 mm,Ln=120.44 mm,Lp=70 mm,NXP=-4 mm,此时,喷射系数μ取得最大值0.39.

