核电厂用860 t阻尼器试验台架性能设计分析与仿真

邓 冬,熊冬庆,邓天勇,詹佳硕,郑向阳

(1.环境保护部核与辐射安全中心,北京 100082; 2.中国船舶重工集团公司第719研究所,武汉 430064)

目前,现有二代加CPR1000和CNP1000等核电厂的大型阻尼器为600 t,三代AP1000和CAP1400核电厂的大型阻尼器为860 t,这些大型阻尼器包括蒸汽发生器、稳压器和主泵的阻尼器[1],仅有德国LISIGA公司和法国QUIRI公司能够设计制造.

核电厂用860 t阻尼器综合试验台架主要为核电站主设备(蒸汽发生器、稳压器和主泵)用阻尼器[2-3]实施动态和静态试验[4].综合试验台架可进行包括摩擦阻力、闭锁速度、旁通速度、振动、过载和抗疲劳试验等[5-6].

综合试验台架最重要的部分是液压伺服系统,伺服系统的性能决定了整个试验台架的性能.通过对位置伺服系统和力伺服系统的特性进行分析,并对力伺服系统进行AMESim仿真,验证伺服系统设计能够满足试验台架的性能要求.

阻尼器综合试验台架有两个并行的伺服系统——位置伺服系统和力伺服系统.当进行低速阻力以及闭锁速度试验时,采用位置伺服系统;当进行高频振动试验时,则采用力伺服系统.力伺服系统和位置伺服系统相互独立,不同时工作.位置伺服系统和力伺服系统的加载控制如图1所示.

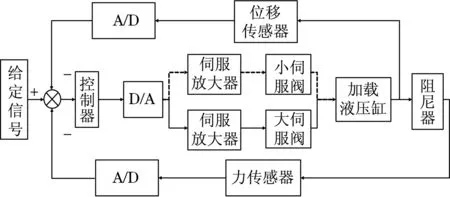
图1 位置伺服系统和力伺服系统加载控制框图Fig.1 Loading control diagram of positionservo system and power servo system

1 位置伺服系统分析

伺服阀的流量连续性方程为

(1)

式中:Kq为伺服阀流量增益;KC为伺服阀流量-压力系数;Xv为阀芯位移;PL为负载压降.

液压缸流量连续性方程为

(2)

式中:AP为活塞面积;S为液压缸作用面积；Xp为活塞杆位移;Ctp为液压缸的泄漏系数;Vt为加载缸腔、阀腔和管道的总容积;βe为有效体积弹性模量.

液压缸的输出力与负载力的平衡方程为

(3)

式中:mt为活塞及负载折算到活塞上的总质量;Bp为活塞及负载的粘性阻尼系数；Ff为液压缸所受的摩擦力.

偏差指令信号为

(4)

式中:Ur为指令电压信号;Uf为反馈电压信号.

位移传感器方程为

(5)

式中:Ks为位移传感器增益.

伺服放大器输出电流为

(6)

式中:Ka为放大器增益.

伺服阀传递函数为

(7)

式中:KSV为伺服阀放大系数；ωmf为伺服阀的固有频率;ξmf为伺服阀的阻尼比.

根据上述计算分析,位置伺服控制系统简化框图如图2所示.

图2 位置伺服控制系统传递函数框图Fig.2 Transfer function diagram of position servo control system

位置伺服控制系统传递函数框图中各参数定义及数值取值，如表1所示.

表1 位置伺服控制系统传递函数参数Tab.1 Transfer function parameter of position servo control system

由传递函数框图可知,加载缸位移Xp对位移指令的开环传递函数为

GK(s)=

或

GK(s)=

(8)

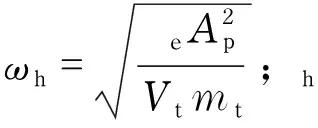
综上可得,位置伺服控制系统的开环传递函数为

(9)

位置伺服控制系统在负反馈下修正的闭环传递函数为

(10)

系统无扰开环传递函数和闭环传递函数Bode图如图3所示.

图3 位置伺服控制系统Bode图Fig.3 Bode diagram of position servo control system

位置伺服控制系统的两个二阶转折频率分别为100和211 Hz,系统幅频特性比其对数相频特性先交于横轴,系统稳定.在无扰动时,给定信号幅值衰减严重,相位滞后较大,需要在校正控制环节加入较大的比例环节,同时为了减小稳态误差,需要加入一定的微分环节.

2 力伺服系统分析

力传感器方程为

(11)

式中:Kf为位移传感器增益;FN为阻尼器受到的加载力.

伺服阀传递函数为

(12)

分析可知力伺服控制系统如图4所示.

图4 力伺服控制系统传递函数框图Fig.4 Transfer function diagram of power servo control system

力伺服控制系统传递函数框图中各参数定义及数值取值，如表2所示.

由传递函数框图可知,加载液压缸输出力F对力指令的开环传递函数为

(14)

代入相关数据得开环传递函数为

(15)

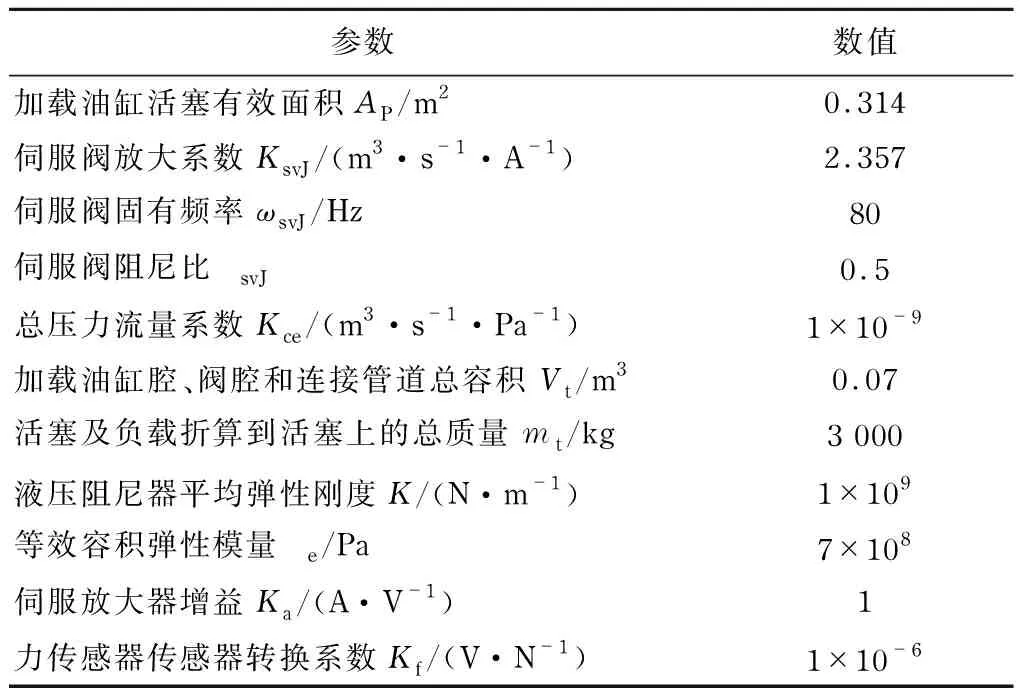
表2 力伺服控制系统传递函数参数Tab.2 Transfer function parameter of power servo control system

闭环传递函数:

系统开环传递函数和闭环传递函数Bode如图5所示.

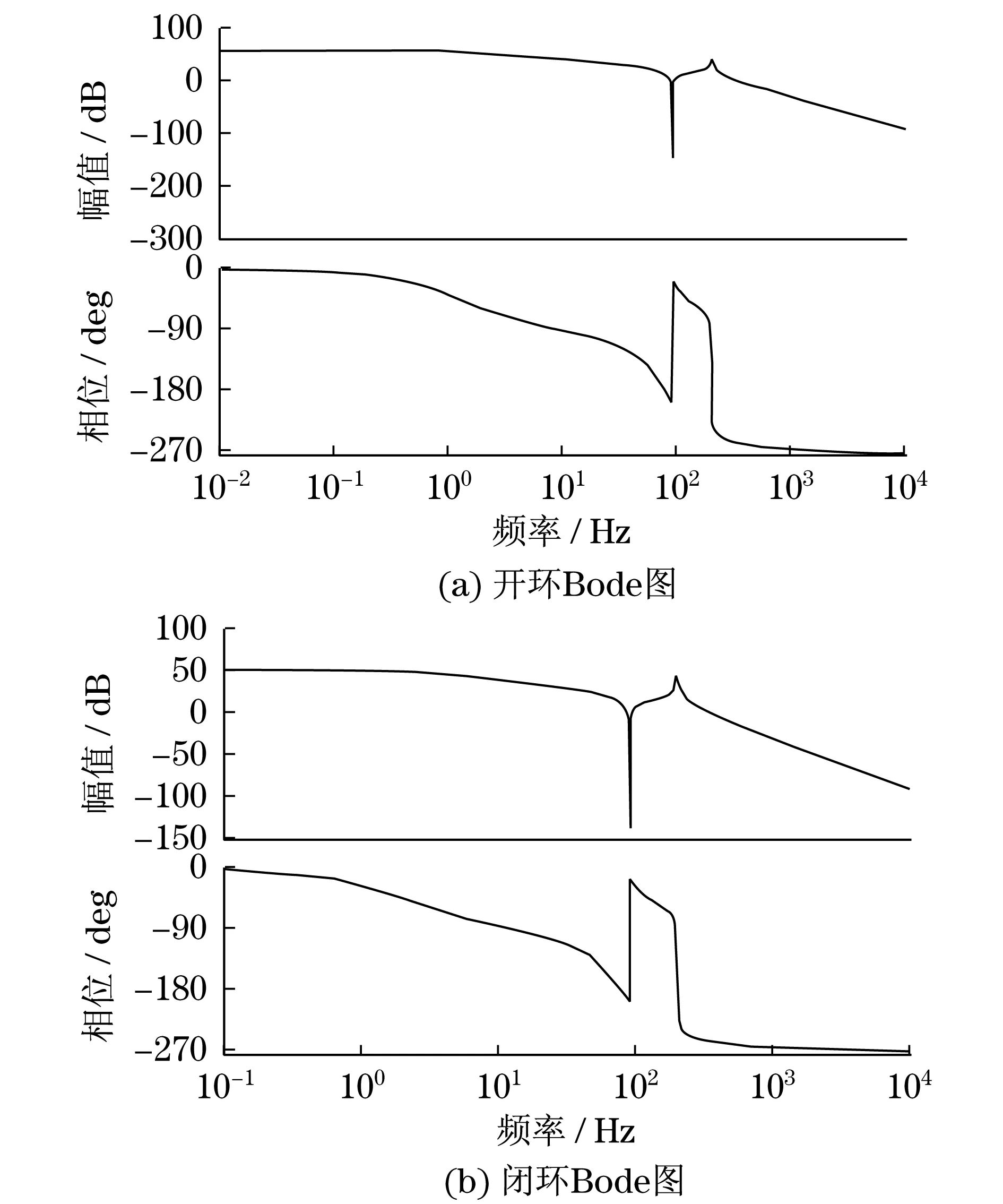
图5 力伺服控制系统Bode图Fig.5 Bode diagram of power servo control system

力伺服控制系统的分母上的两个个二阶转折频率分别为80 Hz和236 Hz,分子上的二阶转折频率为107 Hz,显然系统幅频特性比其对数相频特性先交于横轴,系统稳定.力位置控制系统在2 Hz的给定信号下,幅值衰减严重,相位滞后过大,系统的快速性能和稳态误差较差,需要在校正过程中加入合适的比例环节.

3 力伺服系统仿真

力伺服系统建模如图6所示.

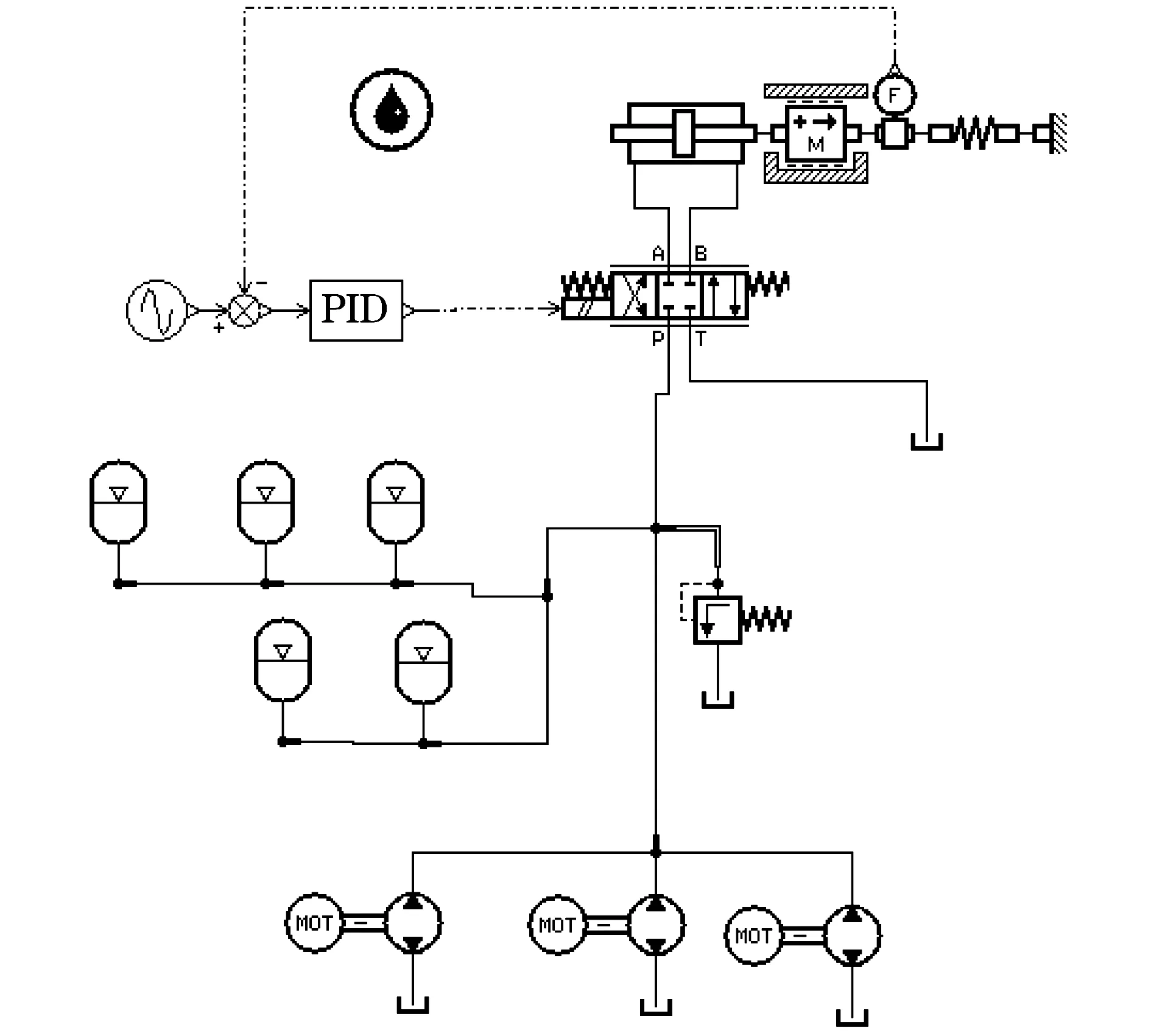
图6 力伺服系统仿真模型Fig.6 Simulation model of power servo control system

为了模型的简化,仿真模型中用4个200 L和1个150 L的蓄能器代替了实际系统设计中进油路19个50 L的蓄能器,其预充压力按照设计过程设定为16 MPa,蓄能器起始充油到气体压力为29 MPa.根据恒压变量泵的工作特性,即没有达到设定的压力值,其可以作为一个定量泵处理,模型中使用3个排量为180 mL/rev的定量泵,代替实际系统中的3个恒压变量泵.系统输入信号为幅值为5×106N,频率为2 Hz,其仿真结果见图7.通过PID校正后的系统能够较好地跟踪2 Hz的正弦曲线,即能够满足试验台架性能指标的要求.

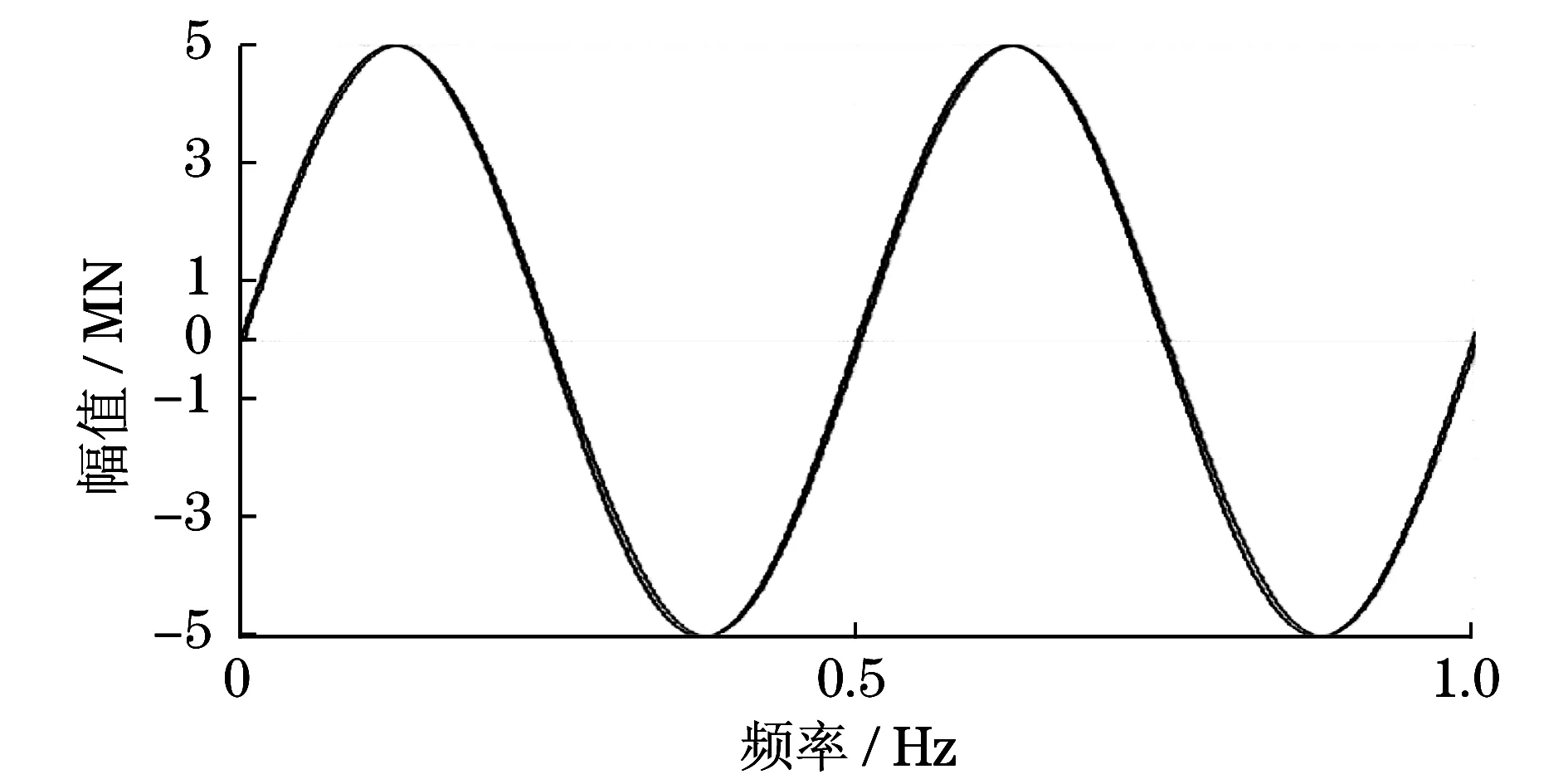
图7 力伺服系统仿真结果Fig.7 Simulation diagram of power servo control system

4 结论

三代AP1000和CAP1400核电厂中蒸汽发生器、稳压器和主泵等主设备用的大型阻尼器为860 t,综合试验台架主要为这些大型阻尼器实施动态和静态试验,包括摩擦阻力、闭锁速度、旁通速度、振动、过载和抗疲劳试验等.综合试验台架最重要的部分是液压伺服系统,伺服系统的性能决定了试验台架的性能.通过对位置伺服系统和力伺服系统的特性进行分析,并对力伺服系统进行AMESim仿真,验证伺服系统的设计满足试验台架的性能要求.