载荷相互作用效应的非线性累积损伤模型
王 欣,柳明珠,蔡福海,梁吉飞,杜剑威,孙 新
(1.大连理工大学 机械工程学院,辽宁 大连 116024; 2.大连理工常州研究院有限公司,江苏 常州 213164)
在工程中,许多机械结构都承受复杂变幅载荷的作用,疲劳失效是机械结构最常见的失效形式之一[1].在设备的工作过程中,结构内的疲劳损伤以累积的方式逐渐增加,在达到疲劳状态之前,如果不提前修复,可能会造成严重的事故和经济损失.因此,对于结构设计和安全使用,疲劳寿命预测非常重要[2].
目前,描述疲劳累积损伤的模型主要分为两类:线性累积损伤理论和非线性累积损伤理论[3].线性累积损伤理论的代表是Miner法则[4],由于其概念简单和易于实现,在工程中得到广泛利用.然而,在变幅载荷作用下,载荷历史(如载荷的加载顺序、载荷的相互作用)对疲劳累积损伤影响较大[5].由于Miner法则不考虑载荷历史的作用,导致其寿命预测的精度较低.
为了克服Miner法则的缺点,学者们提出了许多非线性累积损伤模型,主要分为以下几类:基于损伤曲线法模型、基于连续损伤力学模型、基于材料物理性能退化模型、考虑载荷相互作用效应模型、基于能量法模型[6].叶笃毅等[7]基于材料韧性随疲劳损伤演化规律,提出了一种非线性累积损伤模型(以下简称叶笃毅模型),由于其形式简单、物理意义明确,在工程上得到了一定的应用.由于该模型未能考虑载荷之间的相互作用,其寿命预测还存在着一定的误差.近些年,一些学者对该模型进行了改进,取得了一定的效果[8-9].
本文通过前、后两级载荷应力比的平方来表现损伤演化过程中载荷相互作用效应的影响,将其引入叶笃毅模型,改进了后一级载荷的损伤演化方程,建立了剩余疲劳寿命预测的修正模型[10].通过文献中两种材料的试验数据,验证了改进后模型在两级载荷加载下的有效性.
1 叶笃毅韧性耗散模型
一般认为,疲劳累积损伤是材料力学性能退化的一个不可逆过程,因此,可以选择材料的力学参量(弹性、塑性、强度和韧性等)作为机械结构的损伤参量.叶笃毅等[7]通过大量的试验发现,在材料的疲劳损伤过程中,韧性变化最为明显.因此,叶笃毅等[7]基于材料韧性随疲劳损伤演化规律,提出了一种非线性累积损伤模型,其损伤演化方程如下:
(1)
根据等效损伤原理,由式(2)和式(3)推得两级载荷作用下,第1级载荷σ1作用循环次数n1后,第2级载荷σ2的剩余寿命n2/Nf2为

表1和表2给出了45#钢、A1-2024铝合金两种材料的光滑试件,在两级载荷作用下疲劳试验数据[11-12]与Miner法则、叶笃毅模型剩余寿命预测结果比.可以看出,叶笃毅模型预测的结果比Miner法则更接近于试验值,表明了叶笃毅模型的合理性.

表1 45#钢两级加载试验数据及各模型剩余寿命预测结果Tab.1 Two stage loading test data of 45# steel and prediction results of residual life of each model

表2 铝合金Al-2024两级加载试验数据及各模型剩余寿命预测结果Tab.2 Two stage loading test data of Al-2024 aluminium alloyand prediction results of residual life of each model
2 改进的非线性模型
虽然叶笃毅模型比Miner法则寿命预测的精度更高,但从表1和表2可看出:其寿命预测的结果与试验值还存在一定的误差.在高低载荷作用下,寿命预测结果要比试验值大;在低高载荷作用下,寿命预测结果要比试验值小.
(5)


当总损伤度为1时,试件发生破坏,令式(8)D=1可推得,两级载荷作用下,第1级载荷σ1作用循环次数n1后,第2级载荷σ2的剩余寿命n2/Nf2为
(9)
以此类推,也可计算出多级载荷作用下的总损伤度以及最后一级载荷σi的剩余寿命ni/Nfi:

3 数据结果对比
为验证改进后模型的合理性,本文仍以45#钢、Al-2024铝合金两种材料的试验数据为例,对比了Miner法则、叶笃毅模型及本文提出的改进模型剩余寿命的预测结果,如表3、表4、图1和图2所示.从结果对比可看出,本文提出的改进模型剩余寿命预测结果比其他两个模型更靠近试验值,表明了改进模型的合理性.
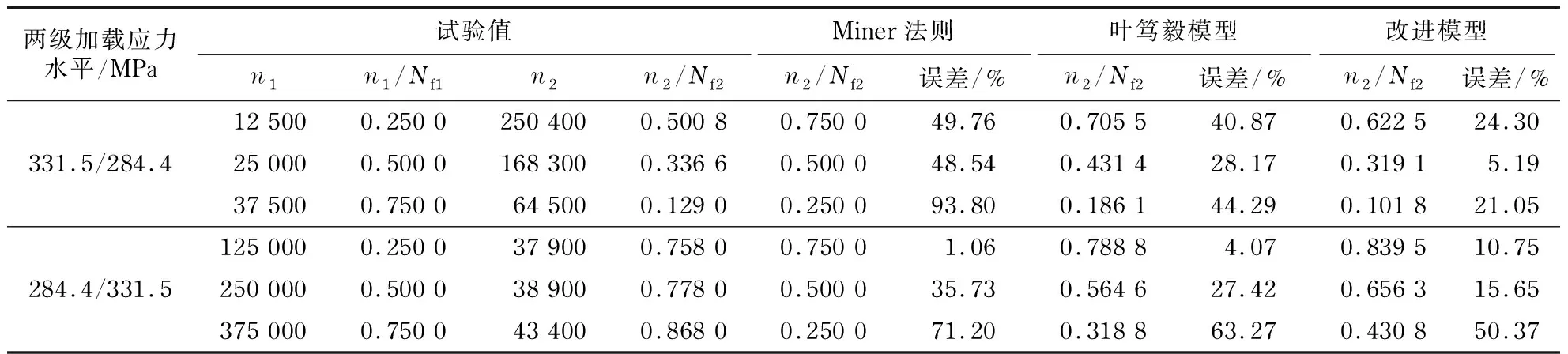
表3 45#钢两级加载试验数据及各模型剩余寿命预测结果Tab.3 Two stage loading test data of 45# steel and prediction results of residual life of each model

表4 Al-2024铝合金两级加载试验数据及各模型剩余寿命预测结果Tab.4 Two stage loading test data of Al-2024 aluminium alloyand prediction results of residual life of each model

图1 45#钢两级加载试验数据及各模型剩余寿命预测结果Fig.1 Two stage loading test data of 45# steel and prediction results of residual life of each model
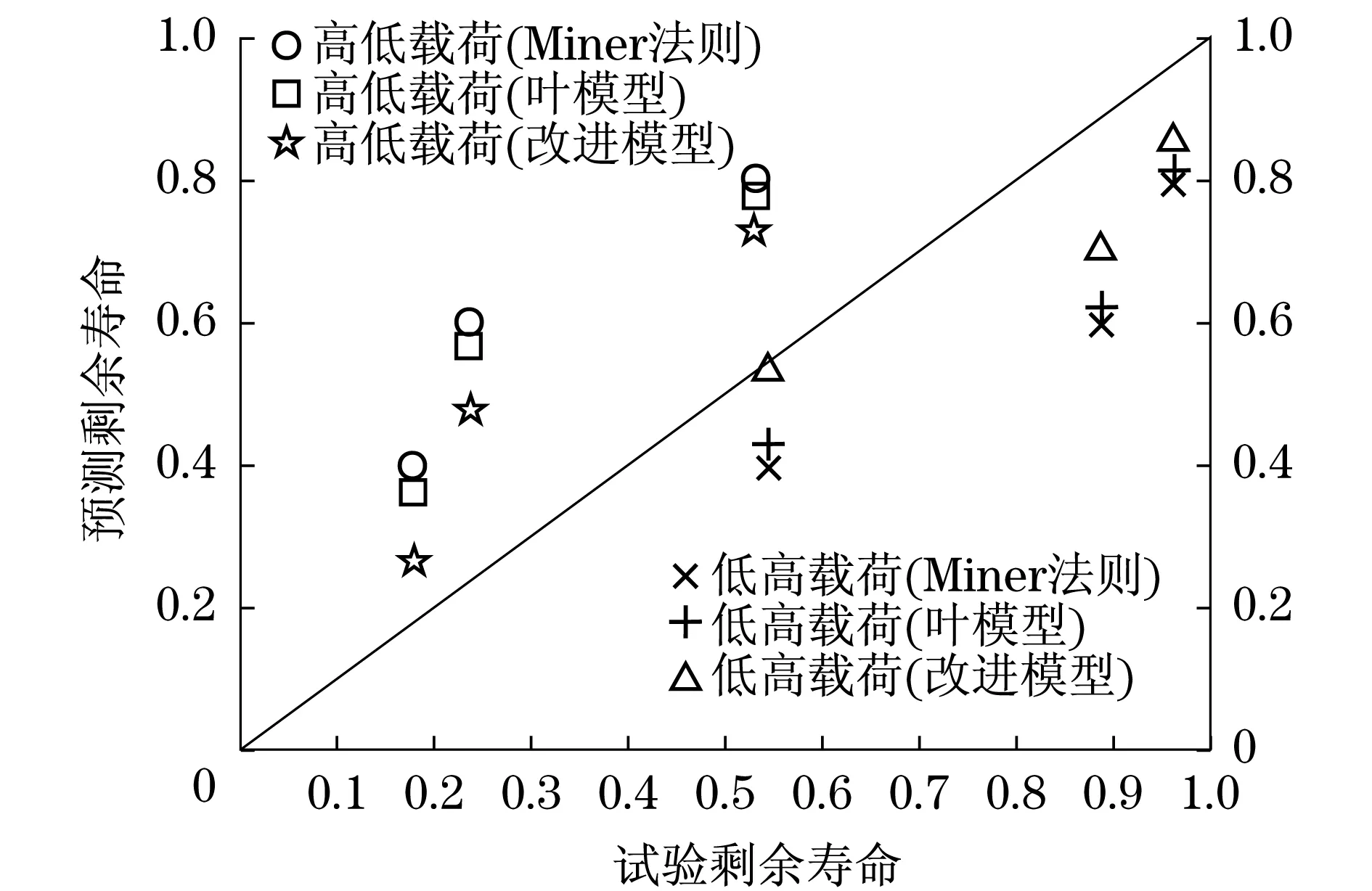
图2 Al-2024铝合金两级加载试验数据及各模型剩余 寿命预测结果Fig.2 Two stage loading test data of Al-2024 aluminium alloyand prediction results of residual life of each model
4 结语
在变幅载荷作用下,载荷历史(例如:载荷的加载顺序和载荷的相互作用)对疲劳累积损伤影响较大.Miner法则由于未考虑载荷历史的作用,导致其寿命预测的精度较低.叶笃毅韧性耗散模型仅考虑了载荷加载顺序的影响,其寿命预测精度虽有提高,但仍存在一定的误差.
本文分析了模型的误差,在此模型基础上,通过前、后两级载荷应力比的平方来表现损伤演化过程中载荷相互作用效应的影响,将其引入此模型,改进了后一级载荷的损伤演化方程,建立了剩余疲劳寿命预测的修正模型.通过文献中两种材料的试验数据,验证了改进后模型在两级载荷加载下的有效性.

