城市环境BDS/MEMS-IMU组合导航的模型误差抑制方法

郝雨时，徐爱功，隋 心，潘 峰

(1.辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2.北京卫星导航中心，北京 10094)

0 引言

中国正在运行和正在建设的北斗卫星导航系统(BeiDou navigation satellite system，BDS)是全球卫星导航系统(global navigation satellites system，GNSS)的重要组成部分[1]，可全天候、全天时提供高精度位置信息，误差不随时间累积，但需保证信号实时跟踪，且信号采样率低、抗差性差、易受环境影响。相对于卫星导航定位系统，惯性导航系统(inertial navigation system，INS)具有短时间精度较高、可提供丰富的导航参数、采样率高、自主性强的优势，其劣势是误差随时间累积较快，无法长时间提供高精度导航参数。BDS/INS组合导航系统结合2种技术的特点，实现优势互补，BDS抑制INS误差累积，INS辅助BDS信号跟踪，保证长时间高精度、高频率、较丰富的导航参数解算。随着微机电系统(micro-electro-mechanical system，MEMS)及惯性测量单元(inertial measurement unit，IMU)技术的发展，MEMS-IMU以体积小、成本低的优势，在大部分组合导航应用中逐渐取代了高成本的光纤或激光惯导[2]，基于BDS/MEMS-IMU组合导航理论研究具有深远意义。

扩展卡尔曼滤波(extended Kalman filter，EKF)常用于组合导航数据处理，其精度依赖于系统、观测模型精度，以及精确噪声统计信息[3]。对于城市环境BDS/MEMS-IMU组合导航应用，常出现卫星数目少甚至无可视卫星的情况，单卫星导航定位系统无法保证连续高精度定位，同时MEMS-IMU误差累积迅速，导致模型精度难以维持，噪声统计信息不易获取，采用传统EKF难以实现参数最优解算。有关控制异常误差影响的方法有抗差卡尔曼滤波[4]、自适应卡尔曼滤波和抗差自适应卡尔曼滤波[5-8]等。文献[4，7-9]提出将自适应抗差滤波理论从不同角度对卡尔曼滤波进行改进，在组合导航应用中取得了明显效果。

本文在系统噪声参数优化方面，通过比较当前预测残差协方差与理论误差协方差，调谐系统噪声协方差一步预测；在观测噪声参数优化方面，本文根据BDS观测值观测情况，评估观测噪声影响，对观测噪声参数进行进一步调谐，提升组合导航模型状态参数解算精度。

理论上，BDS/MEMS-IMU紧组合具有可行性，紧组合可充分利用BDS观测值信息，不受可视卫星数量约束，误差补偿能力高于松组合；但在城市环境应用中，BDS信号无法保证连续跟踪，卫星信号频繁失锁且受多路径效应影响，观测值存在较大的观测噪声，较大的观测噪声会通过系统模型对状态估计产生正反馈而导致滤波发散，状态参数远离真值[9]。从滤波器设计的应用角度来说，选取一个理论上次优的滤波器比理论上最优但易受模型误差影响而崩溃的滤波器更为重要。因此，本文讨论的BDS/MEMS-IMU组合导航模型采用松组合的形式，即观测量为来自2个系统解算的位置及速度的差值，其中BDS定位方式采用基于相位的动态相对定位。

1 BDS/MEMS-IMU组合导航模型

本节介绍的BDS/MEMS-IMU组合导航模型包括系统模型及观测模型。推导过程在文献[10-12]中均有详细介绍，不作为本文的研究重点。

1.1 系统模型

本文讨论的BDS/MEMS-IMU系统模型采用姿态漂移角误差模型，由INS位置rc、速度vc及漂移误差角ψ的导航方程扰动分析获得[13-14]，表达式为

(1)

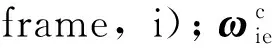
(2)

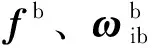
1.2 观测模型

1.2.1 位置误差观测方程

IMU与BDS接收机物理位置关系如图1所示。

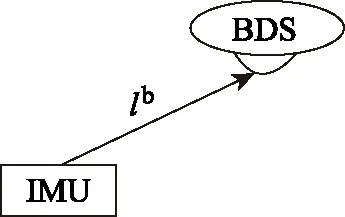
图1 IMU与BDS接收机位置关系

图1中lb为载体坐标系下杠杆臂。p系下由IMU推算的BDS接收机位置天线相位中心位置表达式为

(3)

假定lb无标定误差，对式(3)做扰动分析得

(4)

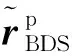
(5)

式中εr为BDS位置观测噪声。BDS/MEMS-IMU位置误差观测方程为

(6)

1.2.2 速度误差观测方程

对式(4)求导[15]得

(7)

假定杠杆臂无标定误差，对式(7)做扰动分析得

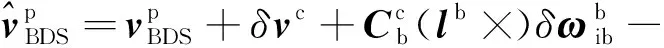
(8)

(9)

式中εv为BDS速度误差，以BDS序贯解算过程中北东地速度标准差取代。BDS/MEMS-IMU速度误差观测方程为

(10)

2 噪声参数优化

卡尔曼滤波是一种线性最小方差估计方法[13]，广泛应用于多源数据融合解算。对于城市环境BDS/MEMS-IMU组合导航应用过程，模型结构、状态参数及噪声统计信息存在未知部分，且存在较大的系统及观测噪声。为实现参数最优解算，需优化相关噪声参数(如系统噪声协方差矩阵Qk、观测噪声协方差矩阵Rk及初始误差协方差矩阵P0)，以实现状态参数最优化解算。

P0反映滤波初始状态误差水平，影响滤波解算初期收敛速度，对全局影响较小，无需作为参数优化的重点。Qk反映状态参数的噪声强度[14]，Rk反映观测值噪声强度，二者大小影响卡尔曼增益的计算，即决定状态参数解算对系统模型及观测模型的依赖程度[15]。因此优化Qk、Rk为滤波器噪声参数优化的重点。

2.1 系统噪声参数优化

系统噪声协方差矩阵Qk无法直接控制，可利用自适应因子α调谐Pk一步预测。协方差一步预测表达式为

(11)

(12)

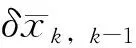
(13)

式中α的隶属函数表达式为

(14)

式中：c0为常数，可取1～1.5。若α小于1，系统预计正常，系统噪声协方差预计接近真实的噪声特性；反之，系统预计异常，可根据式(11)将Pk，k-1适当放大，则卡尔曼增益增大，抑制了状态参数解算受系统模型误差影响的程度。

2.2 观测噪声参数优化

预测残差可反映系统模型精度及稳定性，其前提是观测值精度可靠，或观测噪声特性较精确已知；但实际应用中，观测值无法长期保证稳定的精度，即Rk不能符合真实的噪声特性。若式(14)探测到系统异常，经过式(11)计算，导致滤波解算依赖观测值精度，易扩大观测噪声的影响。较大观测噪声对状态估计产生正反馈可导致参数估计发散不可逆[17]。

对于理想卡尔曼滤波器，给出一致的估计误差与不确定度也能得到状态参数稳定估计[18]，考虑带宽限制下的观测噪声时间相关性及同步误差，适当放大Rk是有必要的，一般要给出相应标准差2到3倍的状态不确定度。令

(15)

式中：εr、εv分别为BDS解算的位置及速度的观测噪声，即BDS序贯解算过程中的误差协方差，反映BDS解算过程的滤波精度，其大小往往小于真实绝对误差；ρ为抗差因子。美国国家海洋电子协会(National Marine Electronics Association，NMEA)认为，位置精度衰减因子(position dilution of precision，PDOP)、模糊度固定成功率P、可视卫星数N、εr、εv皆可直接或间接反映车载卫星定位解算质量。本文根据NMEA协议，构建ρ的隶属函数，量化以上指标对观测噪声的影响，隶属函数构建流程如图2所示。

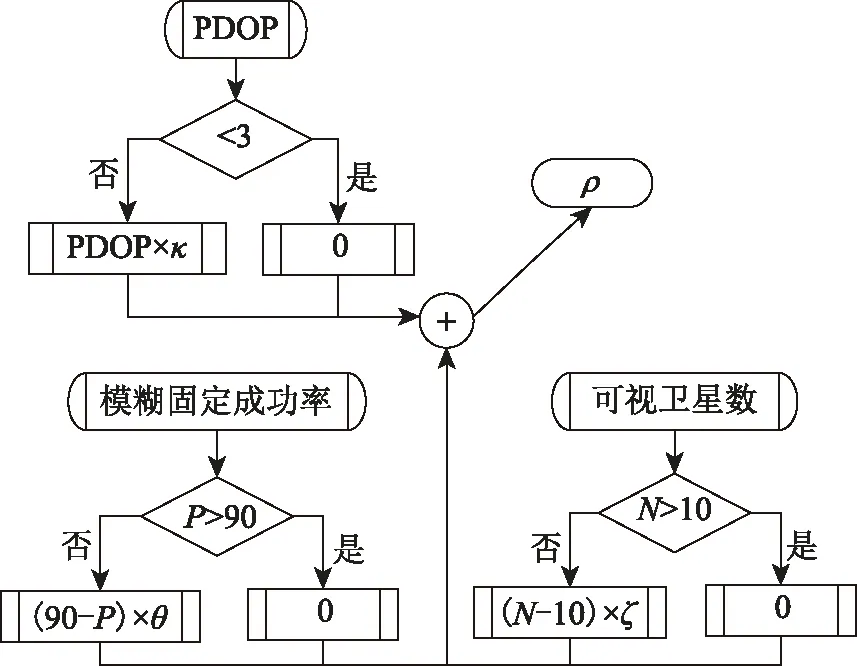
图2 观测噪声参数优化

ρ的作用在于根据观测值质量调谐观测噪声协方差。κ、η、ζ及θ为量化参数，用以量化观测数据质量，可取0.1～0.5，以保证Rk在适当的范围内放大。

需要说明的是，为避免较大观测噪声通过系统造成估计偏差，需在执行式(13)之前先进行观测噪声协方差优化。

3 实验与结果分析

3.1 实验方案与环境

为测试噪声参数优化机制对BDS/MEMS-IMU组合导航的改善程度，本文设计2种实验方案，比较其主要导航参数(平面位置、姿态角)的滤波精度及与参考结果的相对偏差。

方案1)利用标准EKF处理BDS/MEMS-IMU组合导航数据；

方案2)利用加入噪声参数优化机制的EKF处理BDS/MEMS-IMU组合导航数据。

参考结果由光纤级别的定位定姿系统(position and orientation system，POS)提供，其GNSS系统采用GPS/BDS/GLONASS三系统，IMU级别为光纤级。参考POS系统及本文测试的POS系统(BDS/MEMS-IMU)精度指标如表1所示。

表1 精度指标

图3表示 BDS观测值情况及定位观测值结果质量。

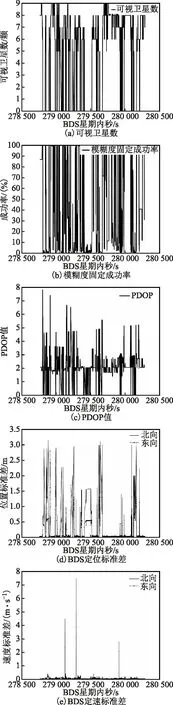
图3 BDS定位质量

图3中，参考POS系统的IMU及BDS/MEMS-IMU系统的IMU采样率皆为200 Hz，GNSS采样率为1 Hz，采样时间为1 527 s，空间里程8 715.094 m。根据BDS观测情况，可以看出城市环境下，BDS系统解算频繁出现异常，如PDOP值过大、模糊度固定成功率低等。

3.2 结果与分析

2种方案的滤波收敛结果如图4所示。

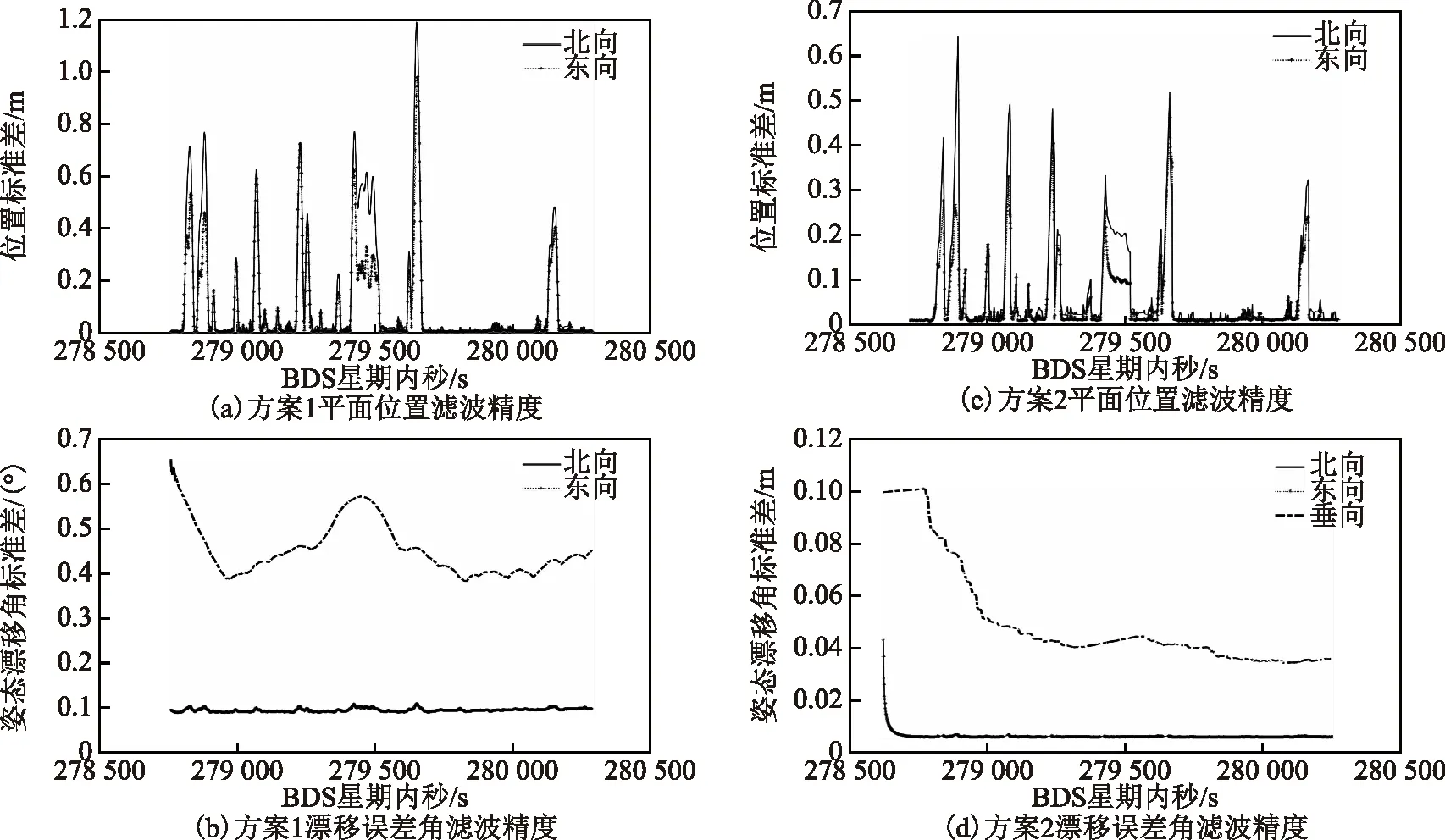
图4 2种方案滤波精度

由图2～3可知，相对于标准EKF，加入噪声参数优化机制可以提升组合导航模型的滤波精度，平面位置及漂移误差角的稳态值有降低趋势。对于平面位置滤波精度，2种方案的平面位置滤波收敛结果均有6个尖刺点，通过对比其大小，可以认为方案2提升了恶劣环境下平面位置的滤波精度，提高约2/3。对于漂移误差角滤波精度，方案1的平面漂移误差角约为0.1°，垂向漂移误差角约为0.5°；方案2的平面漂移误差角为0.01°，垂向漂移误差角约为0.047°。通过对比2种方案的滤波收敛情况，可以认为加入采样噪声参数优化机制能够提升恶劣环境下组合导航模型平面位置的滤波稳定性，且明显提升本文讨论的导航模型的姿态滤波稳定性。

2种方案的相对偏差如图5所示。由图5可知：对于平面位置，结合噪声参数优化机制后，误差峰值有所降低，出现尖刺点比率明显降低；对于姿态误差，横滚角及俯仰角精度均有提升，航向精度提升明显。可以认为噪声参数优化机制的介入对参数解算稳定性及精度提升均有意义。

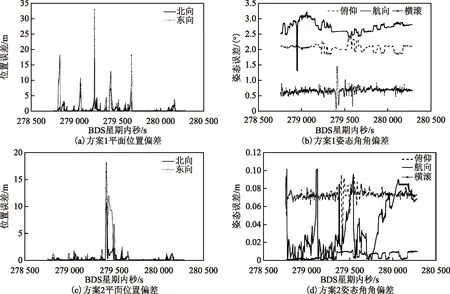
图5 2种方案结果偏差

4 结束语

本文讨论了一种噪声参数优化方法，包括基于分析预测残差的系统噪声参数优化及基于BDS观测情况的观测噪声参数优化方法，应用于城市环境下车载BDS/MEMS-IMU组合导航模型。实验结果证明，对于城市环境车载BDS/MEMS-IMU组合导航应用，加入噪声参数优化机制可提升模型的稳定性，提升位置、姿态参数的精度。