室内移动定位与测图系统的高精度标定

李帅鑫，李广云，符京杨，李明磊，王 力

(1.信息工程大学 地理空间信息学院，郑州 450000；2.信息工程大学 数据与目标工程学院，郑州 450000)

0 引言

室外环境下，基于惯性导航/卫星导航组合的移动测量系统发展相对完善；而在室内环境下，受障碍物、墙体的遮挡，卫星导航系统等基于无线信号的导航定位手段无法正常工作[1]。基于视觉的导航定位方法具有不依赖信号源、环境鲁棒性强、地图表达直观等特点，因此更适合用于室内定位与移动测图。深度相机(red-green-blue-depth，RGBD)由1个彩色镜头、1个深度镜头以及1个测距仪组成，是一种能同时获得环境影像与深度数据的传感器。以Kinect为代表的RGBD相机具有价格低廉、数据获取能力强等特点，近年来已成为计算机视觉、移动机器人、组合导航和室内移动测量等领域的研究热点[2]；但RGBD相机本身也存在深度测量精度不高、测距范围有限、可视角较小等缺陷，文献[3]对Kinect距离量测误差进行测试，指出其误差最高可达1.5 cm：因此，研究克服RGBD相机测量缺陷的传感器组合方案及其标定方法具有重要意义。

基于飞行时间(time of flight，TOF)的RGBD相机误差模型主要分为4类：第1类是图像的暗噪声和相机散射噪声，可用滤波方法消除[4]；第2类是外部噪声，包括目标表面纹理的影响、多路径效应、温度和湿度的影响等；第3类是设备自身的噪声，如预热时间、积分时间等[5]；第4类是设备系统误差，包括设备各部件间的相对位姿和相机的主点偏移、焦距、畸变系数等内参数。对组合系统的标定主要是对第4类误差模型建模。

对RGBD相机的标定，文献[6]提出两步法(two-step independent，TSI)，即先利用干涉仪等高精度测距仪器对相机测距仪进行标定，再将其结果作为已知量解算内参。文献[7]提出一步法(one-step independent，OSI)，该方法利用光束法平差，将多视角影像、垂直影像及垂直距离量测值一并代入约束方程中联合求解。文献[8-9]在TSI和OSI的基础上进行改进，提出改进的两步法(two-step dependent，TSD)，采用多角度和垂直方向的连续影像标定相机内参，并反算垂直方向的距离，得到测距仪的标定参数。文献[10]对这3种方法进行了分析，指出OSI和TSD标定精度差异不大，均优于TSI；TSI存在焦距估计量偏小、深度估计量偏大的问题。文献[11]提出采用红外光源照射得到红外影像，直接对深度相机进行标定。文献[12]提出采用空间直线定长约束标定深度相机。文献[13]根据红外影像与深度影像的配准关系分别对彩色镜头和红外镜头进行标定，并在标准长度基线场对深度量测值做进一步标定。

对传感器安置参数的标定主要指各传感器相对位置和姿态参数的解算。对组合系统的标定可在单相机内参数已知的基础上通过光束法平差完成[14]。即将各传感器同一时刻获取到的相同标志在空间中位置不变作为约束，求解传感器间相对位姿。文献[15]详细综述了多传感器组合系统的标定方法，将其总结为两步法和一步法。两步法即先对传感器单独标定，再带入整体优化方程中求解相对位姿；而一步法则将传感器安置参数和内参数一并加入优化方程中，采用光束法平差联合求解。文献[16]提出利用物方空间坐标已知的标志点后方交会来进行多相机相对位姿求解的方法。文献[17]采用直接线性变换(direct linear transformation，DLT)解算激光扫描仪(terrestrial laser scanner，TLS)和相机的相对位姿。

本文针对RGBD相机/TLS组合的室内移动测量系统传感器参数的标定问题展开研究，提出一种较为快速、高精度的系统性标定方法。该方法分为RGBD相机标定和传感器安置参数标定2部分；对RGBD相机的标定采用附加空间定长约束的两步法；对传感器安置参数的标定，提出基于重投影误差最小约束的改进直接线性变换法，以保证扫描仪在角点提取精度不高时标定结果的鲁棒性。通过分别求解各相机与扫描仪的安置参数，完成各传感器间相对位置关系的标定，最终实现组合系统获取的影像和点云数据的整体映射。

1 标定方法

1.1 方法概述

针孔相机模型如图1所示。

图1 针孔相机模型

图1中：u、v为像素坐标；p、q为图像上2个点；O-ijk为相机坐标；f为相机焦距；P、Q为相机坐标系下2个物方点。组合系统内各坐标系及其变换关系如下：

(1)

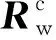
(2)

(3)

式中f为镜头焦距。

(4)

4)组合系统中传感器C1和C2间的刚体变换为

(5)

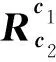
(6)

(7)

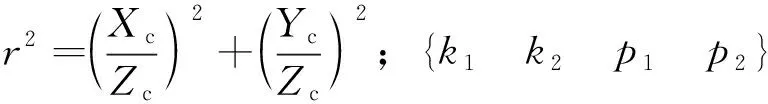
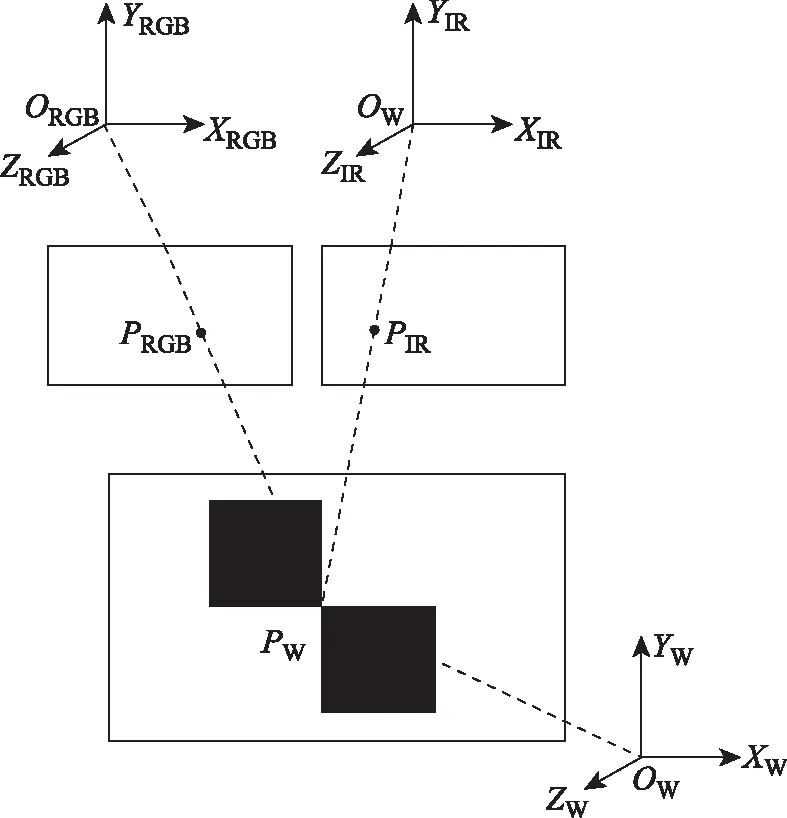
图2 坐标系位置关系

图2中：Ow-XwYwZw为物方坐标系；ORGB--XRGBYRGBZRGB为相机彩色镜头坐标系；OIR-XIRYIRZIR为红外镜头坐标系；P为标志点。组合系统各传感器坐标系位置关系如图3所示。

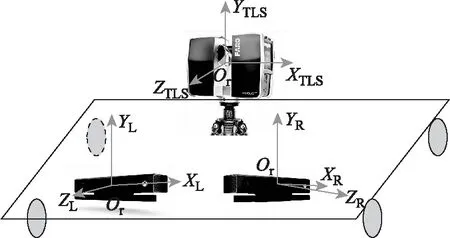
图3 组合系统传感器位置关系

实现多深度相机组合定位与测图系统的联合标定本质上即统一系统中各传感器坐标系。标定分为RGBD相机自标定和传感器安置参数标定2个部分(如图4所示)。

图4 标定流程

具体步骤如下：

1)RGBD相机标定。对Kinect 2.0 RGBD相机采用张正友标定法[17]对彩色和深度相机分别进行标定，得到各相机的内方位元素和畸变系数初值。之后根据定长直线约束条件对深度相机内参进行优化。最后采用光束法平差求解2个镜头间的外参并对镜头内参进行整体优化。

2)传感器安置参数标定。从激光扫描仪得到的点云中提取棋盘格角点，建立扫描仪坐标系与Kinect坐标系的相对位置关系，并采用直接线性变换求解，得到传感器安置参数初值。之后根据重投影误差最小的约束条件进行整体优化。

1.2 RGBD相机标定方法

文献[18]利用棋盘格标定板与相片的单应性变换关系对相机进行标定，较传统标定方法具有使用灵活、操作简便等特点，且标定精度优于自标定方法；因此本文将张正友标定法的结果作为初值，采用空间直线定长约束进一步优化。

1.2.1 基于空间定长直线约束的深度镜头标定方法

由式(1)～式(7)可得

(8)

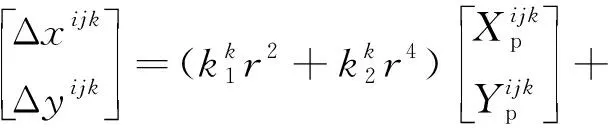
(9)

式中：i为示棋盘格特征角点编号；j为拍摄的图像编号；k为相机编号；sijk为尺度因子，其值为相机k拍摄第j幅图像时特征点i所对应深度值的倒数。实际计算中由于切向畸变远小于径向畸变，因此可直接忽略切向畸变的影响，即

(10)

由式(10)得像素坐标与像方坐标的变换关系为

(11)

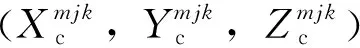
(12)

根据该约束条件，RGBD相机标定时目标函数I可写为

(13)

将式(13)写为误差方程形式

v=CΔ-L

(14)

根据最小二乘原则，可求解非线性误差方程

Δ=(CTPC)-1CTPL

(15)

式中：Δ为相机内参改正数；C为非线性方程在初值位置的雅克比矩阵；L为I的估值；P为权阵。由于量测精度与距离有关，则可根据直线2个端点深度值平均数的倒数定权，具体形式可表示为：

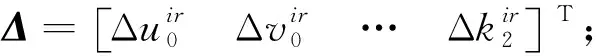
1.2.2 彩色镜头内参估计与相对位置估计

将深度镜头内方位元素作为已知量，反算棋盘格角点在相机坐标系下的坐标，并代入彩色图像共线条件方程中，求解彩色内参和镜头间相对位置[19]，最后根据重投影误差最小的约束条件采用光束法平差对解算结果进行整体优化[20-21]。

根据文献[15]所述，相机相对位置估计的准确性受控制点空间布局的影响；因此为保证精度，在采集图像时应尽量保证棋盘格位于图像中部2/3的区域，避免整个标定板都位于图像的边角位置。

1.3 传感器安置参数标定方法

由于RGBD相机测量视角较小，且对于距离较远的区域量测精度较低，为保证测图的效率和精度，采用由2台Kinect2.0相机和1台三维TLS的组合定位与测图系统方案。相机分别拍摄2个方向以保证足够大的探测范围，TLS用于较远目标深度的探测。TLS拥有360°视角，因此可将各传感器坐标统一到TLS坐标系下。

直接线性变换是根据共线条件方程的线性变换解算外方位元素的一种方法[17]，其特点是不需要变换初值，更适合计算大旋角外方位元素。需要指出的是该方法要求至少6对以上不共面的控制点，因此标定标志的设计需要特别注意；另外，直接线性变换依赖于空间点的精度，若个别物方控制点存在偏差，该方法的标定精度将大大下降：因此本文提出一种改进的直接线性变换方法，将直接线性变换结果作为初值代入光束法平差模型中做整体优化。

1.3.1 直接线性变换法

1.3.2 基于重投影误差最小的优化方法

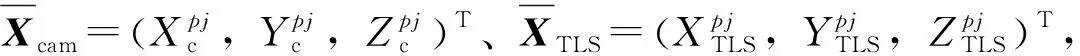
(16)

(17)

(18)

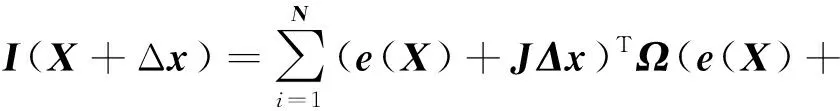
(19)

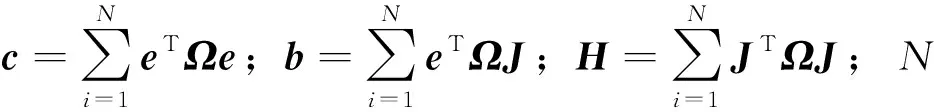
-b=HΔx*

(20)

将X=X+Δx*作为初值迭代计算，直到结果收敛。需要说明的是：求位姿矩阵的雅克比矩阵实际上就是在6维变换空间求导；但由于旋转矩阵对加法不封闭，不能构成线性空间，因此求导时需要利用李群SO(3)和对应的李代数SE(3)[23]。

2 实验与结果分析

2.1 实验方案

实验对一个由2台Kinect 2.0 RGBD相机和1台Faro Focus3D 120激光扫描仪组成的组合定位与测图系统进行标定(如图5(a)所示)；标定板采用尺寸为6个×8个网格的棋盘格板，网格边长90 mm。Kinect的原始彩色、深度、红外影像数据通过Kinect和OpenCV库获取得到(如图5(b)和图5(c)所示)，标定系统采用C++编程实现。

数据采集时，每帧数据包含彩色、深度和红外影像，分别提取彩色、红外影像棋盘格角点。选择对角线上的4个影像点交叉互连，在一幅图像上构成2个定长约束。第j次拍摄的点n在彩色、红外影像上的像素坐标分别为(unjc，vnjc)和(unji，vnji)，对应深度值(dnj，dnj)。相机内参数和传感器安置参数的精度通过反算得到的棋盘格角点像点坐标与量测的像点坐标的偏差来评定。

图5 实验设备和角点提取

2.2 RGBD相机标定

实验分别对2个Kinect 2.0 RGBD相机进行标定，共采集到50组有效影像数据，每组数据中包含红外影像、深度影像和彩色影像，且保证所选定长线段的端点处有深度值。RGBD相机标定结果及精度如表1～4所示，其中旋转外参数用罗德里格斯旋转向量的3个分量r1、r2、r3表示，平移外参数由tx、ty、tz表示。

表1 左侧Kinect内参数及精度

表2 左侧Kinect 2个镜头外参数 mm

表3 右侧Kinect内参数及精度

表4 右侧Kinect 2个镜头外参数 mm

由表可以看出，标定精度在影像坐标系的2个方向均可达到0.2个像素左右，符合精度要求，在安置参数标定时可作为已知量带入解算。

2.3 组合系统安置参数标定

实验采用Faro Focus3D 120 TLS和Kinect组合平台采集数据。为保证直接线性变换解算初值的精度，采用3个×4个网格的4个棋盘格标定板，并使各标定板互不平行。棋盘板的布设尽量使角点均匀分布于影像中。采用多棋盘格板生长算法[24]提取彩色影像中的棋盘格角点，利用点云角点提取方法获得点云中的棋盘格角点，角点提取结果如图6所示。为了消除传感器偶然误差，实验共进行10次，取平均结果为最终标定结果。

图6 多标定板角点提取

实验中，安置参数的精度由内符合精度评价，即计算观测像点与估计像点间的坐标差。传感器安置参数解算结果均值如表5所示，平均精度如图7所示。其中：φ、θ、ψ分别为横滚角、俯仰角、偏航角；tx、ty、tz为平移分量。

表5 组合系统传感器安置参数均值

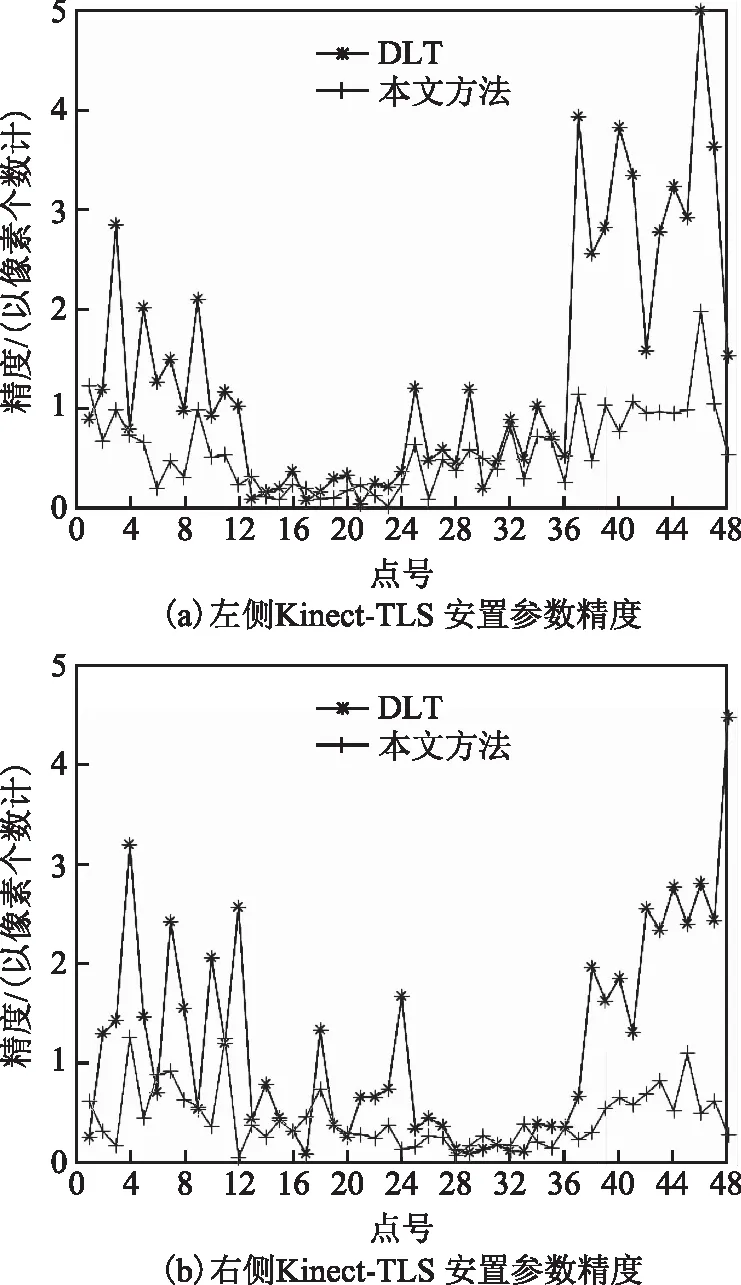
图7 特征点平均精度

图7中深色线表示DLT结果的精度，浅色线表示以DLT结果作为初值进行优化后的精度。由图中可以看出：DLT解算结果在图像2侧点位精度较差，最大可达5个像素，整体起伏较大；优化后精度显著提升，绝大部分点位精度可达1个像素左右，最大不超过2个像素，整体起伏也较为平稳。起伏较大说明存在偏差较大的点，如点云对应右侧影像的2、43、47，这些点受到棋盘格角点提取偏差的影响(如图8所示)而导致重投影误差很大。优化后这些点位精度提升，可见该算法对角点提取精度具有一定鲁棒性。Kinect相机单个像素的物理尺寸约为0.008 mm，因此安置参数标定结果的精度完全满足后期影像间的拼接与建图要求。

图8 点云角点提取误差

3 结束语

本文提出了一套针对多RGBD相机组合定位与测图系统安置参数的较为快速、高精度的标定方案。整体处理流程包括RGBD相机内参数及杆臂值标定和组合系统传感器安置参数标定2部分。其中RGBD相机的标定采用基于定长直线约束的标定方法；针对安置参数的标定提出优化的直接线性变换方法。实验结果表明该标定方案精度可达1个像素左右，符合测图时影像拼接的需求。

本标定方案的意义在于：1)提出对扫描仪特征点提取精度不高时较为鲁棒的安置参数标定方法；2)针对本文的移动测量平台提出了一套完整的高精度标定方案，可快速完成传感器自身及其安置参数的高精度标定；3)将传统直接线性变换法的结果作为整体优化的初值，采用光束法平差进一步提升标定结果的精度，对于其他组合设备安置参数的标定同样具有参考意义。