RBF神经网络辅助的UWB/INS组合导航算法

徐爱功，蔡赣飞，潘 峰，隋 心，郝雨时，刘 韬

(1.辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2.北京卫星导航中心，北京 100094)

0 引言

随着人们在室内环境下的工作与活动时间日益增多，人们对室内定位的需求也随之增大[1]。常用的室内定位技术有蓝牙定位、超宽带(ultra wide band，UWB)定位、超声波定位等。其中，超宽带定位是一种利用非正弦波脉冲来传输信息的无线通信技术，凭借其功率消耗低、穿透能力强等特点，UWB及相关技术广泛应用于室内定位研究[2]。但UWB测距信号抗差性较差，对定位精度影响很大[3]。惯性导航系统(inertial navigation system，INS)是一种不依赖外界环境的自主式导航系统，具有短时间定位精度高、抗干扰能力强等优点[4]。但INS误差会随时间迅速累积而导致定位结果发散。UWB/INS组合既能利用UWB抑制INS误差随时间的累积，又能利用INS弥补UWB输出频率低、信息单一的缺陷，提供高频率、丰富的导航参数信息[5-6]。但在UWB/INS组合导航中，由于室内环境复杂，UWB信号很难保证持续跟踪，当能接收到信号的基站个数较少时，UWB/INS组合导航系统中只有INS系统单独定位，定位结果会很快发散。针对这种情况，一般可以通过采用更高精度的INS传感器或加入其他传感器到组合系统中的方式进行解决，但会增加组合系统的复杂性与成本。因此需要确定一种合适的方法，该方法既可以保证组合系统定位精度的连续性也不需要额外增加硬件的成本。

在UWB/INS组合定位过程中，当UWB信号未中断时，UWB/INS组合定位方法可获得高精度的定位结果，而此时单独INS系统的定位精度会随着时间累积而变差，在此期间，如果能够采用一定的方法确定出单独INS系统的定位结果与UWB/INS组合定位结果之间的映射关系，那么在UWB信号中断后，可以利用UWB信号未中断时所确定出来的映射关系来对单独INS系统的定位结果与UWB/INS组合定位结果之间的差值进行预测，进而对单独INS系统进行位置误差补偿，用INS单系统补偿后的定位结果作为组合系统的定位结果以实现UWB/INS组合系统定位精度的连续性。径向基(radial basis function，RBF)神经网络由较小的单位神经元组成，使用与人脑结构和功能类似的学习算法，它将输入值映射到输出值，可以用来解决建模非常复杂和非线性的随机问题[7-9]。

根据以上分析，可以认为RBF神经网络的理论特性适合于UWB/INS组合定位系统的数据解算过程，可以采用RBF神经网络对UWB/INS组合导航算法进行辅助；因此本文将对基于RBF神经网络辅助的UWB/INS组合导航算法进行研究。

1 UWB/INS组合常规滤波算法

1.1 RTT定位测速

UWB常用的测距方法有信号往返传播时间法(round-trip time，RTT)、到达时间/时间差法(time/time difference of arrival，TOA/TDOA)、信号到达角度法(angle of arrival，AOA)等[10]。其中，RTT测距是通过测量UWB脉冲在基准站和流动站间的往返时间间接完成距离的，这种方法不需要基准站和流动站间的时间同步[11]；因此本文选择利用RTT测距方法解算的结果与INS解算的结果进行组合滤波。RTT测距原理如图1所示。

图1 RTT测距原理

图1中：tm为流动站发送信号的时刻；ts为流动站接收信号的时刻，则流动站与基准站的距离表达式为

(1)

式中：c为光速；di和ti分别是第i个基准站到流动站的距离和标准时间偏差改正；N为基准站的个数。

设N个固定基站的平面坐标为(xi，yi)(i=1，2，…，N)，流动站平面坐标为(x，y)，由此可以推导出

(2)

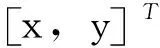
V=AX

(3)

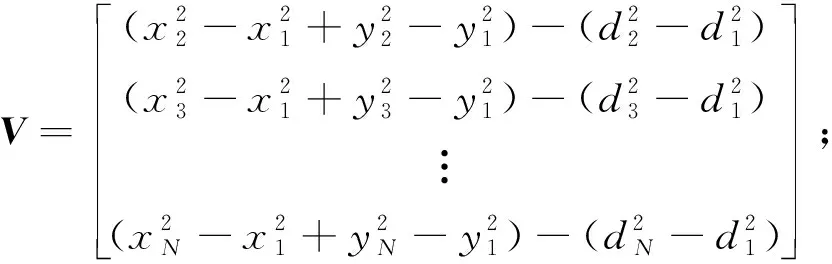
式(3)的最小二乘算法的解[12]为

(4)

式中:P为单位权阵。则UWB流动站速度信息为

(5)

式中：vx，k、vy，k为k时刻UWB的速度；xk+1，yk+1为k+1时刻UWB的位置；xk-1、yk-1为k-1时刻UWB的位置；T为UWB的采样间隔。

1.2 UWB/INS组合导航模型

在UWB/INS组合中，数据融合方法大多基于卡尔曼滤波器。设ΔT为INS的采样间隔，δxk、δyk、δvx，k、δvy，k表示INS在k时刻的位置和速度误差，本文以INS的位置和速度的误差作为状态向量，通过卡尔曼滤波对状态向量进行估计，对组合导航系统进行位置和速度的修正。系统的状态向量可以表示为

Xk+1=FXk+wk

(6)

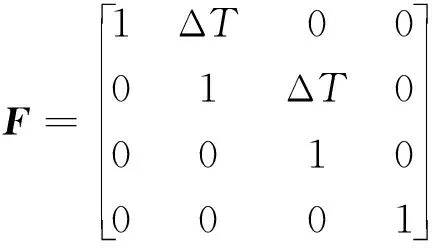
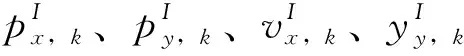
Zk=HXk+ωk

(7)

通过卡尔曼滤波即可对载体的导航信息进行更新[13]，即

(8)

2 RBF神经网络辅助的UWB/INS组合导航算法

2.1 RBF神经网络原理

RBF神经网络是一种具有3层结构的前向神经网络[14]。输入层由一些感知节点组成；隐藏层由仅有一层的节点组成，输入空间经过非线性变化到隐藏空间；输出层由隐藏层经过线性转换得到。相对于其他的神经网络，RBF神经网络的局部调谐神经元能让自身的学习收敛速度更快，紧凑的拓扑结构让自身结构更加简单，单层的隐藏层让自身的表达更容易，这些优点可以让RBF神经网络更好地逼近任意的非线性函数[15]；为此，本文用RBF神经网络来辅助UWB/INS组合导航。RBF网络最常用的结构如图2所示。

图2 径向基神经网络结构

图2中：(x1，x2…xp)∈R为网络的输入矢量；p为输入矢量的个数；φi(x)为径向基函数；Wi∈Rn为输出权矩阵；i=1，2,…,N，N为隐含层神经元个数；Y∈Rn为网络的输出矩阵。本文选取高斯核函数为径向基函数，有

(9)

式中：x为输入矢量；ci、σi为第i个隐含层神经元的中心和宽度。用最小二乘算法求隐含层和输出层间的权Wi，计算公式为

(10)

式中：h为数据中心的个数；q=1，2，…，p；‖·‖为欧式空间的距离范数；cmax为所选取中心的最大距离。

神经元的宽度计算公式为

(11)

2.2 RBF神经网络辅助的UWB/INS组合导航

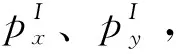
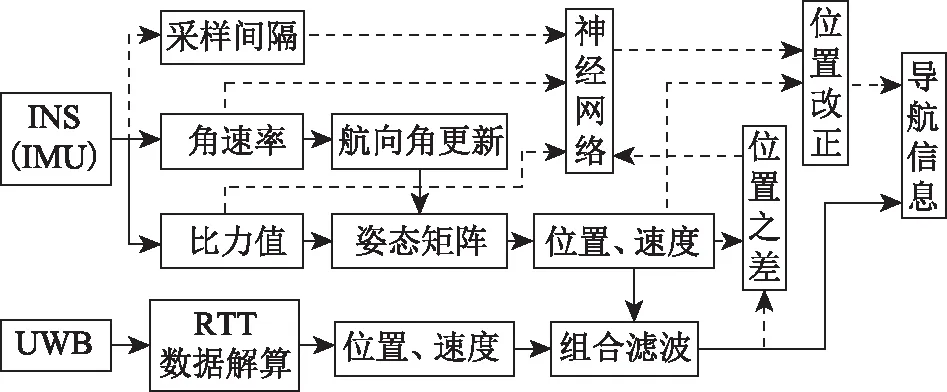
图3 RBF神经网络辅助UWB/INS组合导航结构

3 实验与结果分析

为了验证RBF神经网络辅助的UWB/INS组合导航算法的有效性，在某地下停车场进行了一次模拟实验。其中INS仪器为SBG公司的Ellipse-N-G4A2-B2，输出频率为200 Hz，加速度计随机游走为14.7×10-4m/(s2·Hz0.5)，加速度计零偏为4.9×10-2m/s2，陀螺零偏为0.2 (°)·(s-1)，陀螺角度随机游走为0.18 (°)·(h-1·HZ-0.5)。UWB仪器为Time Domain公司的PulsON400，输出频率为10 Hz，在信号通视条件下测距精度优于10 cm。实验中UWB的3个基准站以接近正三角形的方式进行布设，UWB流动站和基准站在实验过程中无任何遮挡，INS和UWB流动站固定在小车上，小车沿着设定好的轨道运行，小车初始和终止速度设置零，初始的位置为UWB流动站开始运行的坐标值，整个实验过程运行360 s。

为了评价所提算法的性能，本文从绝对误差(absolute error，AE)、均方根误差(root mean square error，RMSE)、提高率(improvment，IP)3个方面对解算的结果进行评价。绝对误差为

AE=|Hi-Li|

(12)

均方根的误差表达式为

(13)

提高率表达式为

(14)

式中：Hi为参考真值；Li为解算的值；i=1，2,…,m，m为UWB采样总数；AER为神经网络补偿之后的绝对误差；AEI为无神经网络补偿的绝对误差。

图4给出了有RBF神经网络辅助和无RBF神经网络辅助的UWB/INS组合导航的轨迹与参考轨迹的整体比较，并在图中依次标出UWB信号在157～162、205～215、270～285 s中断时的局部轨迹。

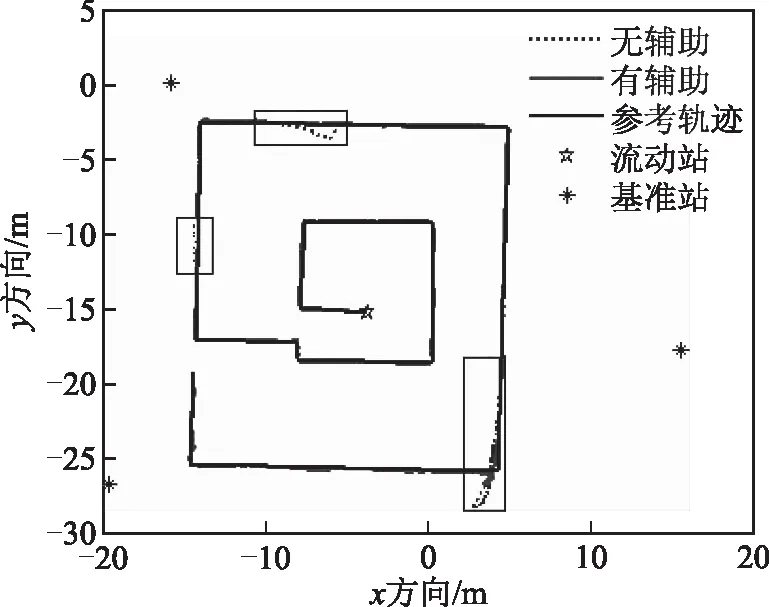
图4 整体轨迹

图5为图4中UWB信号中断后轨迹的放大图，可以看到RBF神经网络辅助的组合导航方法的定位优势非常明显：如果采用无RBF神经网络辅助的组合导航方法，在UWB信号中断后不再对INS进行误差补偿，UWB/INS组合导航解算的定位结果迅速发散；而如果采用有RBF神经网络辅助的组合导航方法，经过RBF神经网络对发散的定位结果进行误差补偿，位置轨迹更接近参考的真值。

图6～8分别为图5(a)、图5(b)、图5(c)对应的位置绝对误差图，通过分析得：在UWB信号中断5 s时，无RBF神经网络辅助的组合导航的定位绝对误差在x和y方向的最大值为0.11和0.08 m，均方根误差为0.05和0.03 m；有RBF神经网络辅助的组合导航的定位绝对误差在x和y方向的最大值为0.08和0.07 m，均方根误差为0.04和0.02 m，提高率分别为23.6 %和26.4 %，可知在UWB信号中断5 s时2种组合导航方法的定位结果都比较好，其中有神经网络辅助的定位精度比无神经网络辅助的定位精度有小幅提升；在UWB信号中断10 s时，无神经网络辅助的定位绝对误差在x和y方向的最大值为0.43和1.05 m，均方根误差为0.18和0.51 m，有神经网络辅助的定位绝对误差在x和y方向的最大值为0.16 和0.18 m，均方根误差为0.07和0.1 m，提高率分别为50.2 %和70.4 %，可知在UWB信号中断10 s时，有神经网络辅助的定位精度有较大提升；在UWB信号中断15 s时，无神经网络辅助的定位绝对误差在x和y方向的最大值为1.15和2.18 m，均方根误差为0.49和1.11 m，有神经网络辅助的定位绝对误差在x和y方向的最大值为0.64和0.67 m，均方根误差为0.24和0.35 m，提高率分别为54.7 %和59.6 %，可知在UWB信号中断15 s时2种组合导航方法的定位误差都较大，虽然有神经网络辅助的定位精度更高，但相对UWB在视距环境下的定位精度，有神经网络辅助的组合导航的定位精度已不能满足人们的定位要求。

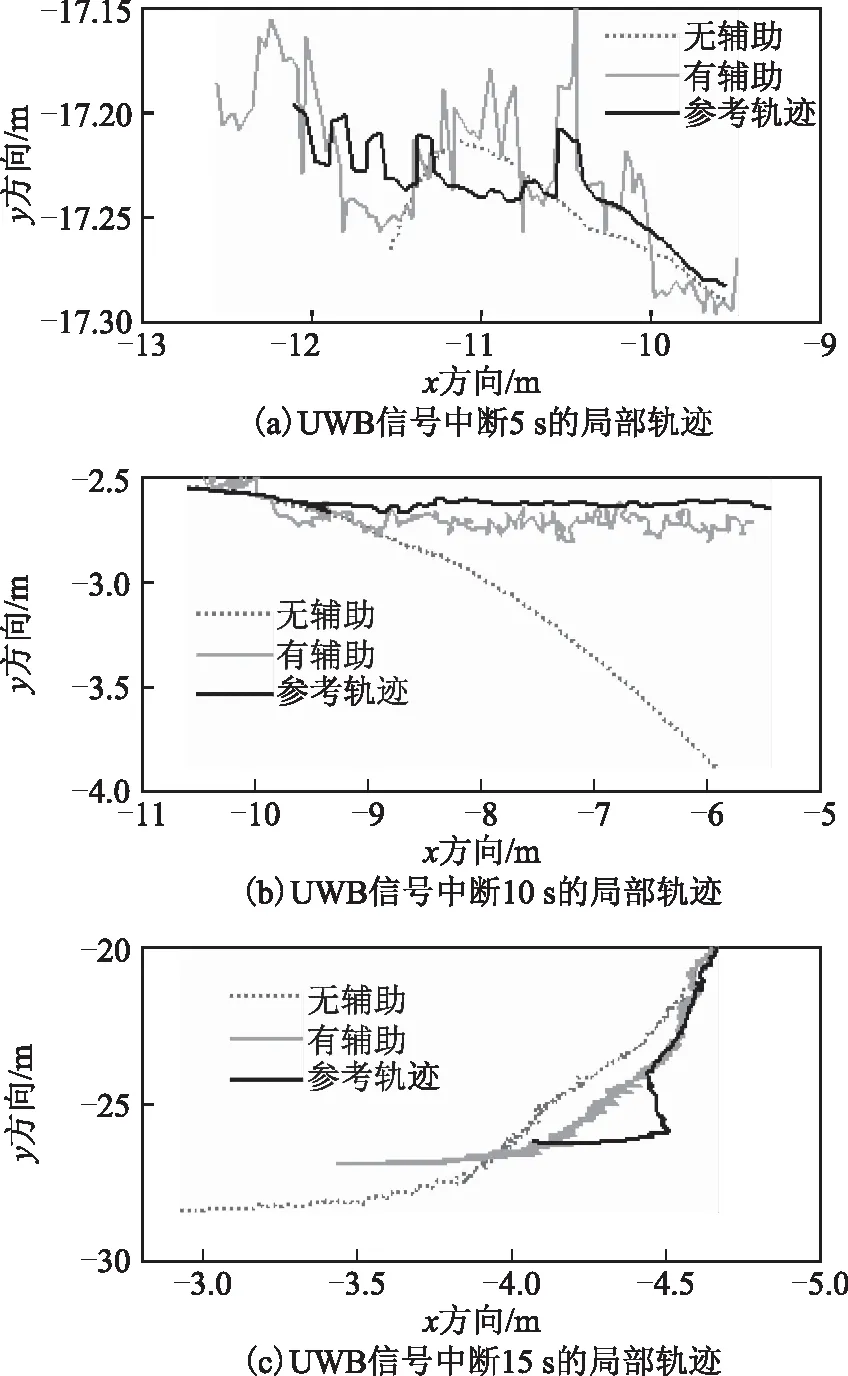
图5 UWB信号中断的局部轨迹

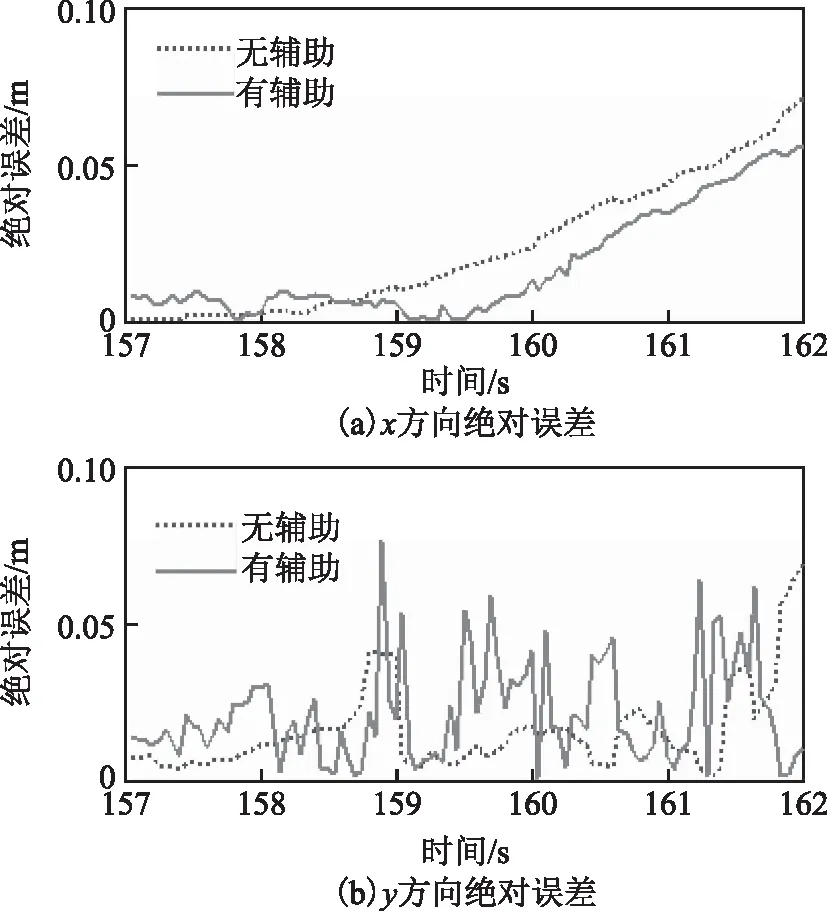
图6 UWB信号中断5 s的绝对误差

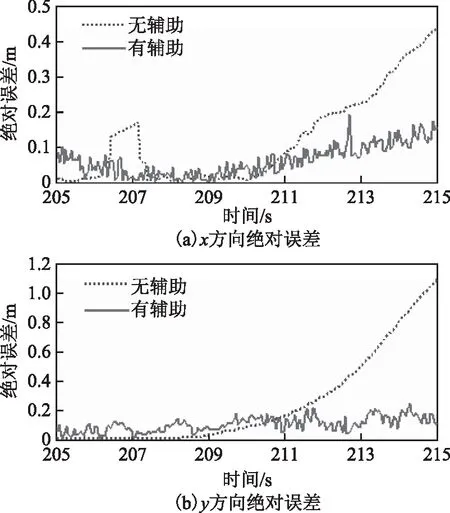
图7 UWB信号中断10 s的绝对误差

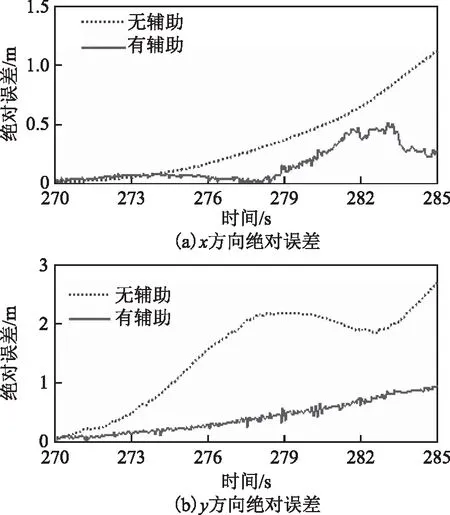
图8 UWB信号中断15 s的绝对误差

综合上述分析可知：要保证定位均方根误差不大于10 cm，UWB信号中断不能超过10 s。另外从图6～8中可以发现，随着UWB信号断开时间的增加，无神经网络辅助的组合导航的定位绝对误差加速增大，虽然经过RBF神经网络补偿的定位绝对误差也开始增大，但增大的速率远慢于无神经网络补偿解算的结果。

4 结束语

本文的目的是在不增加硬件成本的基础上提出一种UWB/INS组合导航方法以提高在UWB信号中断后的定位精度。为此，设计了一种RBF神经网络辅助的导航算法来补偿在UWB信号中断后的UWB/INS组合导航的定位误差，这种方法不需要像传统的UWB和INS数据融合方法一样要对各个传感器的随机误差建模，利用RBF神经网络训练过程中存储的知识对发散的定位结果进行误差补偿，就能为载体提供持续和较高精度的定位信息。实验结果表明在UWB信号中断0～15 s的时间里，所提方法都能够有效提高定位精度。下一步工作包括根据仪器的参数和实际经验提前求得神经网络的各项参数以减少训练的时间，并通过实际的车载数据进一步验证RBF神经网络辅助的UWB/INS组合导航算法的有效性。