采用指纹SD权重的FM两级室内定位方法

屈 阳，万国龙，丛 丽，秦红磊

(北京航空航天大学 电子信息工程学院，北京 100191)

0 引言

基于调频(frequency modulation，FM)广播的定位技术的研究历史可追溯至20世纪90年代，最早是采用移动接收机检测接收到的FM信号的相位进行定位[1]，经过近30年的发展，目前常用的基于FM的定位技术主要有K-近邻定位算法(K-nearest neighbor，KNN)、K-加权近邻定位算法(K-weighted nearest neighbor，KWNN)、高斯过程回归算法(Gaussian process regression，GPR)等技术[2]。公共FM广播信号由于其信号稳定、信号穿透能力强、覆盖范围广、硬件设施要求低等优点[3]而被广泛应用于室内定位。

在使用FM进行室内定位的研究中，FM频道的数量对定位精度有很大影响。文献[3-6]详细研究了FM频道数量的影响，其在采用了76个公共频道和3个信标的前提下，其2σ定位误差为4.71 m。在室内定位中，小范围环境中较少存在指纹模糊的现象，比如单独的一个小房间；大范围环境中，由于室内环境的复杂性，FM信号受室内环境的影响较大，容易造成指纹的模糊，比如整个回字形类的建筑。目前现有的解决方式主要有：1)欧氏距离的计算，比如根据信号的相关性调整欧氏距离[7]、根据当前环境在欧氏距离计算时进行环境自适应参数调整[8]；2)利用信号的传播特性建立信号传播距离与实际物理距离之间的模型[9]；3)定位算法的改进，比如基于距离权重的指纹定位算法[10]。此外，由于FM信号的波长约为3 m，这就造成单纯采用FM信号的定位精度很难超过3 m，由此催生了FM信号与其他信号进行组合定位的研究，常用的有无线保真(wireless fidelity，WiFi)11]信号、蓝牙信号、数字电视地面多媒体广播信号[12]、数字视频广播信号[13]等多种信号源，对于提升定位精度有较大帮助。

本文针对指纹模糊的问题，基于FM频道波动越大，对定位的贡献越大的理论，根据采集到的FM频道指纹的标准差来调整欧氏距离的权重，同时将定位过程拆分为区域定位和精确定位，提出了基于指纹标准差(standard deviation，SD)权重的FM两级室内定位算法。

1 指纹定位简介

指纹定位分为2个阶段：离线阶段和在线定位阶段。离线阶段是采集区域的数据特征，在本文中为采集公共FM广播的信号特征；在线定位阶段是利用定位算法进行用户位置解算。定位过程框图如图1[2]所示。

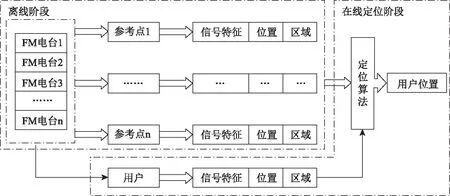
图1 基于指纹的FM广播信号定位方法

2 室内定位算法

2.1 定位描述

在实验区域中，预先测量得到的指纹数据库可以表示为

Ε={(eji，pi)|j=1，…，N，i=1，…，k}

(1)

式中：j为外辐射源个数；i为参考点(reference point，RP)个数；eji为第j个外辐射源在第i个RP的指纹位置；pi为第i个RP的位置，二维空间中，通常pi=(xi，yi)；N为外辐射源的数量；k为参考点的数量；E为指纹数据库。

用户所在位置指纹已知，则可以表示为

E0={(ej0，p0)|j=1，…，N}

(2)

式中：ej0为用户所在位置的第j个外辐射源的指纹位置；E0为用户所在位置的指纹位置。采用合适的定位算法来求解用户所在位置p0。

2.2 定位算法

2.2.1KNN区域定位算法

在KNN区域定位算法中，首先计算用户所在位置的指纹与所有已知点的指纹的欧氏距离，即

(3)

式中:ΔE=[ΔE1，ΔE2，…，ΔEk]为用户与所有已知参考点的欧氏距离的集合，其中ΔEi为用户与第i个RP的欧氏距离。根据欧氏距离选取m(m≥1)个近邻点(通常m不宜过大，应根据实际情况进行选择)，则选取的最小的m个欧氏距离的集合可表示为

(4)

式中h为选择的第h个近邻点。则选取的近邻点所对应的RP的集合可表示为

一个偶然的机会，我在一位收藏家朋友的票夹里看到几枚1944-1946年由晋冀鲁豫边区政府发行的粮票，出于粮食工作的职业本能，我好说软磨，硬是花钱将其买了下来，作为我的藏品。这是很珍贵的历史文物，是我党我军光辉历程的历史见证，反映了粮食工作在中国革命历史时期发挥的重要作用。自此我非常注意军用粮票及有关资料的收集，翻开收藏的军用粮票纪念册，重温我党我军的历史，使我更加热爱和珍惜现在的幸福生活。

P_ΔP={P1∪…∪Ph|h=1，…，m}

(5)

式中Ph为选择的第h个RP。由于每个近邻点均有其区域信息，则区域定位结果的集合可表示为

Z_ΔP={Z1∪…∪Zh|h=1，…，m}

(6)

式中Zh为第h个RP的区域信息。

KNN区域定位选择集合Z_ΔP中个数最多的子集作为区域定位结果，若存在2个不同子集的个数既相同且最多的情况，则将欧氏距离最小的近邻点所在的区域信息作为区域定位结果。

2.2.2KWNN精确定位算法

KWNN定位算法将每个近邻点的位置(xi，yi)用式(3)中的欧氏距离的倒数进行加权后得出用户的位置坐标，即

(7)

式中ε为趋近于0的小数。

2.3 基于指纹SD权重的定位算法

为了增加欧氏距离判断的可信度，提出了基于指纹SD权重的FM两级室内定位算法即标准差权重(standard deviation-weight，SDW)算法。算法的原理如下：

式(3)表征了用户与各参考点之间的欧氏距离，可以看出：电台波动范围越大，其欧氏距离判断越明显，对后续的定位解算贡献也越大。根据已有指纹，计算出FM各个频道的SD，再据此对其赋予权值。假设权值为ωj，则欧氏距离为

(8)

0.2·x·SD1+…+0.2·N·x·SDN=1

(9)

解出x，则对应的第j个频道的权值为

ωj=0.2·j·x·SDj

(10)

式中：SDj为第j个频道的SD值。定位过程分为区域定位和精确定位。将SDW算法计算出的欧氏距离应用于区域定位和精确定位，在区域定位后，根据判定准则，判断是否剔除不属于定位区域的近邻点。

判定准则：当Z_ΔP中个数最多的子集数量超过设定的门限值时，精确定位时仅选择属于定位区域的近邻点。由式(6)可得Z_ΔP，假设Z_ΔP中个数最多的子集为Zn，其个数为n，则：

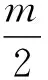
3)若1)、2)均不满足，不执行此准则。

当执行此准则时，此时用户位置坐标可表示为

(11)

3 实验与结果分析

3.1 实验设置

实验区域为北京航空航天大学新主楼F座3楼，实验区域如图2所示。实验数据为使用Tektronix频谱仪采集的FM广播21个频道的数据，实验选择的近邻点个数k为从1到10线性递增，定位区域中指纹数据分为7个区域，共计912个RP(图中仅标注出部分RP)。随机从该指纹数据库中选择45个点作为测试点，余下的点作为RP。实验结果是在50次蒙特卡洛下得出的。

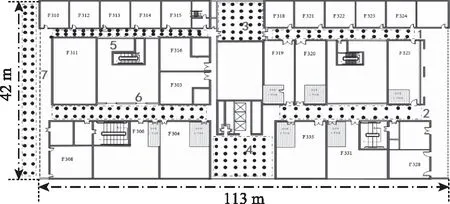
图2 室内实验区域

3.2 结果分析

3.2.1 区域定位精度

此性能指标选择为k取不同值时的平均区域定位精度(如图3所示)。

从图中可以看出，SDW算法对于提升区域定位精度有较为明显的改进，KNN算法区域平均定位精度最低为95.24 %，而SDW算法区域平均定位精度最低为97.02 %。此外，在进行蒙特卡洛时，几乎可以保证区域定位精度不会退化。表1为区域平均定位精度最差时不同k值下的区域定位精度。

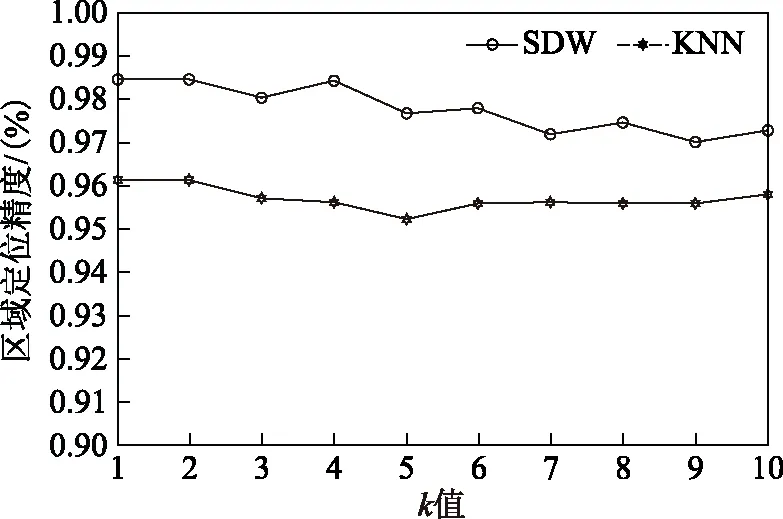
图3 KNN与SDW区域平均定位精度

表1 2种算法在区域平均定位精度最差时分别对应的区域定位精度

3.2.2 精确定位精度

1)1σ和2σ定位误差：

图4和图5分别给出了SDW算法和KWNN算法在50次蒙特卡洛下的1σ和2σ定位误差，其中σ为标准差。表2和表3分别给出了2种算法在50次蒙特卡洛下的1σ和2σ最大、最小和均值定位误差。

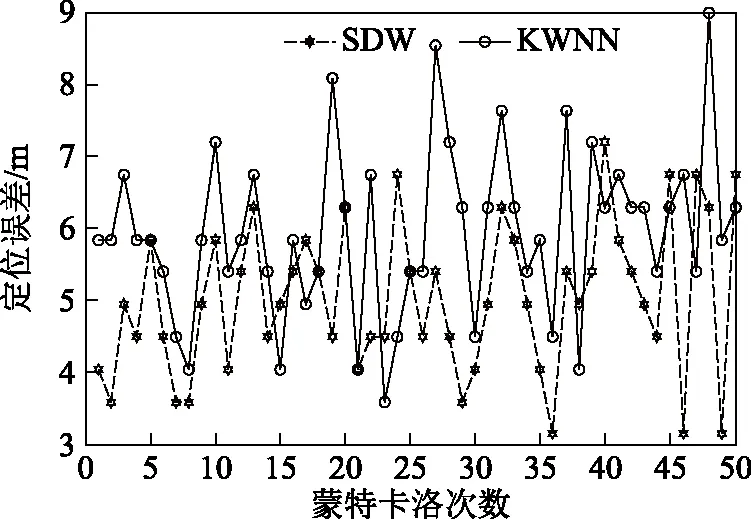
图4 1σ定位误差

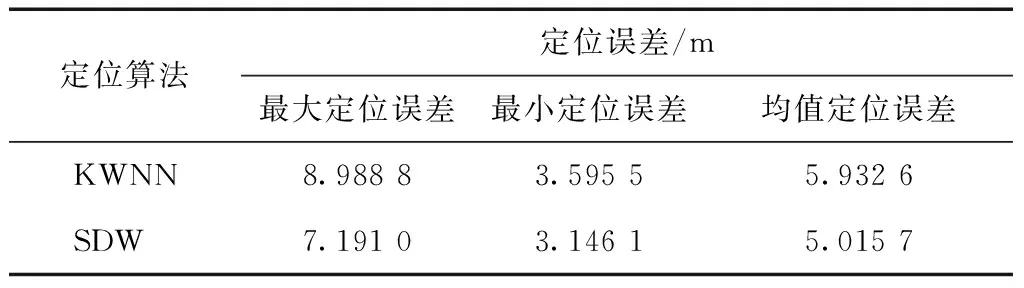
表2 1σ时2种算法对应的最大、最小和均值定位误差

从图4和表2可以看出，SDW算法在50次蒙特卡洛下，1σ定位误差在绝大部分情况下定位误差得到改善，且1σ的平均定位误差相较KWNN算法定位误差改进了0.916 9 m，定位精度提升了15.5 %左右。

图5 2σ定位误差

表3 2σ时2种算法对应的最大、最小和均值定位误差

从图5和表3可以看出，SDW算法在50次蒙特卡洛下，2σ定位误差在绝大部分情况下定位误差得到改善，且2σ的平均定位误差相较KWNN算法定位误差改进了3.847 2 m，定位精度提升了22.6 %左右。

2)平均均方根误差：

表4给出了SDW、KWNN算法在50次蒙特卡洛下不同k值对应的平均均方根误差。

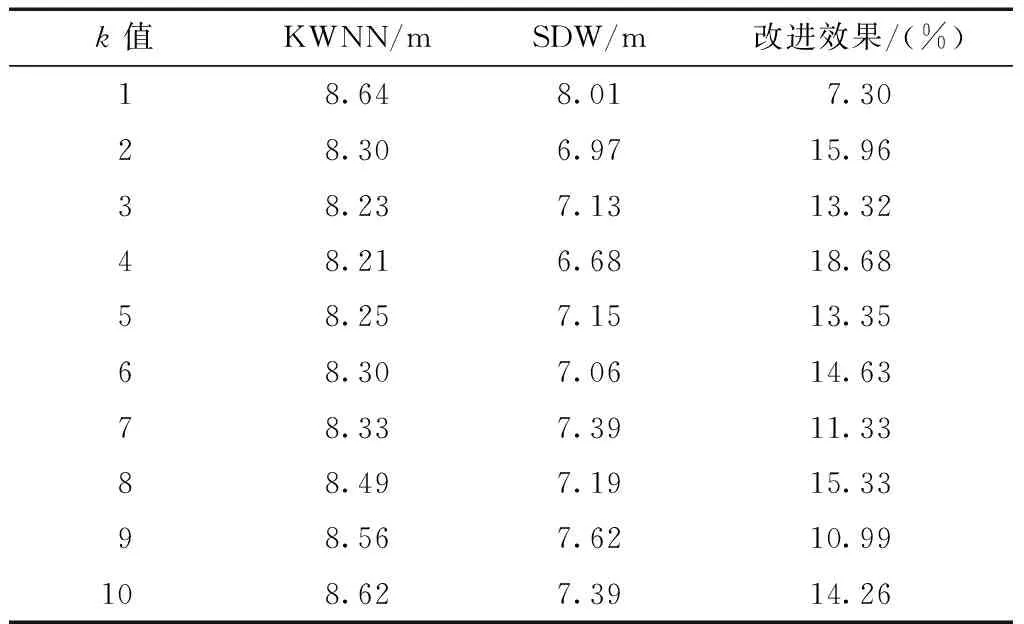
表4 50次蒙特卡洛下的平均均方根误差

从表中可以看出，无论k取何值，其平均均方根误差均得到改善，当k=4时，其平均均方根误差降低了18.68 %。结果表明，SDW算法相较KWNN算法，其定位结果的均方根误差得到了改善。

4 结束语

本文提出了基于SD权重的FM两级室内定位算法，该算法充分利用了FM各个频道的波动情况，有效降低了指纹的模糊性；同时将定位过程划分为区域定位和精确定位，进一步降低了错误近邻点的影响。实验表明：与KNN区域定位算法相比，SDW算法能够提供更加准确的区域信息；与KWNN精确定位算法相比，其1σ、2σ定位误差和平均均方根误差均得到显著改善。因此，SDW算法相较传统指纹定位算法更具优势。下一步研究重点为优化权值及门限的自适应调整。