车用内置式永磁电机直接转矩最大转矩比电流控制

林 立，王 尊，赵乘麟，万炳呈，陈红专，陈鸿蔚

(1.邵阳学院 多电源地区电网运行与控制湖南省重点实验室，湖南 邵阳，422004；2.邵阳学院 信息工程学院，湖南 邵阳，422004；3.湖南耐为电控技术有限公司，湖南 长沙，411100； 4.邵阳市电机厂有限公司，湖南 邵阳，422000； 5.湘潭电机集团有限公司，湖南 湘潭，411100)

新能源电动汽车因其高效、绿色、零排放等特点已越来越被人们所重视。作为传统汽车的取代者，纯电动汽车电机、电池及电控三大关键技术直接影响到汽车的性能。内置式永磁电机因其高效率、高转矩密度等特点，适用于纯电动汽车的驱动。永磁同步电机高性能控制策略常用的有直接转矩控制和矢量控制两种。而直接转矩控制(Direct torque control，DTC)直接针对转矩进行闭环控制，结构简单，转矩响应快，在电动车领域具有较大发展前景。

直接转矩控制是上世纪 80 年代由德国学者Depenbrock 提出的，基本思想是通过对定子磁链定向的方法，直接对电机的定子磁链、转矩与其给定值进行比较，并通过磁链、转矩控制器选择相应的定子电压空间矢量来控制电机[1]。最大转矩比电流(maximum torque per ampere,MTPA)控制策略，是一种在给定电机输出电磁转矩的条件下，定子电流最小的控制策略。有助于提高电机的运行效率，降低损耗，增加电动汽车单次充电续行里程[2-3]。

DTC控制结构简单，转矩响应快，但也存在低速转矩脉动大，开关磁链不固定等不足。针对这些问题目前已有的改进方法有：采用空间电压矢量细分策略优化电压矢量开关表；采用模型预测控制技术、空间电压矢量调制以及自适应滑模控制等方法来实现固定开关频率，抑制转矩脉动的目的。

在传统的DTC控制中，电压矢量开关表只使用到了六个非零电压矢量转矩脉动较大。文献[4]中分析了零电压矢量作用，提出了一种选择零电压矢量的策略，给出了一种新型电压矢量开关表。减少了DTC控制系统开关次数，一定程度上抑制了转矩脉动。文献[5]在传统六个非零电压矢量的基础上采用空间电压调制的方法，新增6个与原非零电压矢量相差30°的空间电压矢量。通过选择与控制参考值最接近的空间电压矢量来实现对传统DTC控制的优化。而文献[6]在此基础上还提出了一种七阶滞环比较器，在输出偏差方向的同时，根据输入偏差的大小输出七个等级的偏差大小，结合空间电压细分策略在保证高系统响应的前提下起到了抑制转矩脉动的作用。

上述方法虽然都能够在一定程度上抑制转矩脉动，但不能固定开关频率，作用效果有限。中国工程院机械与运载工程学部的夏长亮院士，采用矩阵变换器( Matrix Converter，MC)技术，改变传统DTC控制策略的拓扑结构，给出了三种具有应用前景的拓扑结构形式，以实现永磁同步电机系统的高精度、高效率以及高功率密度[7]。

传统的DTC控制中，电压矢量是作用于整个控制周期的，这也是导致转矩脉动的一个重要原因。而模型预测控制就是在传统DTC控制的基础上，将零电压矢量引入到每一次的控制周期内，通过在下一控制周期里通过选择合理的电压矢量或合理分配零电压矢量的分配时间，来调整下一个控制周期内磁链和转矩的变化量，从而起到抑制转矩脉动的作用。

文献[8-9]中根据定子磁链方向将空间分为四个区域，在零电压矢量作用时间一定的前提下，通过计算下一次控制周期内非零电压矢量在区域内的偏转角度，得到下一控制周期里所需的非零电压矢量来实现预测控制。而文献[10-11]则是通过计算下一周期内零电压矢量和非零电压矢量的分配时间，来控制下一控制周期内磁链和转矩的变化量。在此基础上文献[11-12]进一步改进，通过在一个控制周期内引入两个非零电压矢量和一个零电压矢量，通过计算下一周期内三个电压矢量的分配时间来进一步优化预测控制。模型预测控制实现了开关频率的恒定，有效抑制了转矩脉动，但是模型预测控制因需要精确的电机参数而降低了鲁棒性。

电压空间矢量调制(space vector modulation，SVM)是一种在一个控制周期内采用矢量合成的方法，通过对六个非零电压矢量和两个零电压矢量导通时间的合理分配，来合成任一方向的电压矢量。

文献[13-14]中将SVM结合DTC控制，通过转矩PI控制器给定参考磁链位置角增量，对比参考磁链幅值来获取磁链幅值的改变量，以此得到所需的空间电压矢量，通过SVM计算控制周期内逆变桥的导通时间，实现DTC控制系统在恒定的开关频率下运行。文献[15]在此基础上去除转矩PI控制器，通过转矩方程直接计算出负载角，并以此为基础计算出参考磁链的幅值和位置角，实现无差拍的SVM-DTC控制。上述两种方法通过SVM思想，固定开关频率，降低了转矩脉动，但都需要获取精确的电机模型，在定子电阻发生变化或低速运转导致磁链估算误差较大时，控制性能不佳。为改善电机低速运行时的性能，沈阳工业大学电气工程学院的夏加宽教授提出了一种MT坐标系下的DTC控制策略，考虑逆变器残生的电压饱和，采用不同电压矢量对所估算的磁链进行补偿，提高磁链观测精度，提高了永磁同步电机的低速性能[16]。大阪府立大学的Shigeo Morimoto教授在SVM-DTC控制的基础上又给出了一种不需要交轴电感的MTPA算法，提高了电机效率，并且避免了因磁链饱引起交轴电感变化而带来控制偏差[17]。

文献[18-20]中采用滑模控制器取代传统DTC控制中的PI控制器和bang-bang控制器，通过设计磁链和转矩滑模面，电压矢量为控制率，再利用SVM实现对电机的闭环控制。滑模变结构虽然“抖振”问题不能完全解决，但具有较高的鲁棒性，有一定的发展前景。

传统DTC控制最主要的问题就是低速转矩脉动较大，通过Simulink软件搭建永磁同步电机DTC控制数学模型，在模型仿真的基础上分析DTC控制转矩脉动产生的原因，并在基础上探讨最适用于的电动汽车领域的DTC优化策略。

1 内置式永磁同步电机数学模型

1.1 三相静止坐标系下的数学模型

如图 1中以电机定子三相绕组的方向建立三相静止坐标系，为简化分析现做如下假设：1)忽略电机铁芯的饱和；2)不计电机中的涡流和磁滞损耗；3)电机中的电流为对称的三相正弦波电流。在此假设上得到电机的数学模型为[21-22]

图1 永磁同步电机物理模型Fig.1 The physical model of a permanent magnet synchronous motor

图中：ua、ub、uc为三相电压；ia、ib、ic为定子三相电流；ψf为永磁体磁链。

电压方程：

(1)

磁链方程：

(2)

转矩方程：

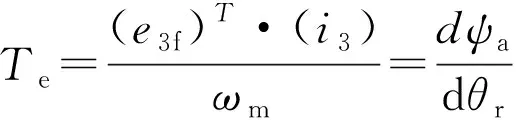
(3)

运动方程：

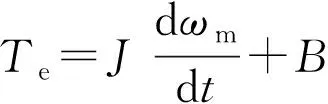
(4)

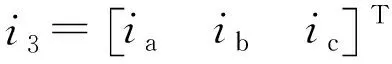
从式(1)-(4)可以看出三相静止坐标系下的电压和磁链微分方程的系数是随着转子位置变化而周期性变化，属于一种非线性、多变量、强耦合的系统，分析求解难度大，为简化分析过程常对电机各参数矢量进行坐标变换[23]。

1.2 两相静止坐标系下的数学模型

将电机静止三相坐标系的向量转换到以A相绕组方向的为ɑ轴，垂直于ɑ轴方向为β轴的静止两相坐标系上来。将向量从静止三相坐标系转换到静止两相坐标系的过程称之为CLARK变换，其变换矩阵C32如下：

(5)

图2 永磁同步电机两相静止坐标系模型Fig.2 Two-phase static coordinatesystem model of PMSM

经CLARKE变换后得到永磁同步电机两相静止坐标系模型，据图 2得电机数学模型为

图中：uα、uβ、iα、iβ、定子电压及电流的ɑ、β轴分量。

电压方程：

(6)

磁链方程：

(7)

转矩方程：

(8)

式中：ψα、ψβ为定子磁链的ɑ、β轴分量；ψfα、ψfβ为永磁体磁链静止两相坐标分量；Lα、Lβ为静止两相坐标系轴向等效定子电感；np为极对数。

在此坐标系下，电机的模型方程实现降阶，但电压和磁链微分方程的系数仍然是随着转子位置变化而周期性变化，因此再对模型进行两相旋转坐标系变换。

1.3 两相旋转坐标系下的数学模型

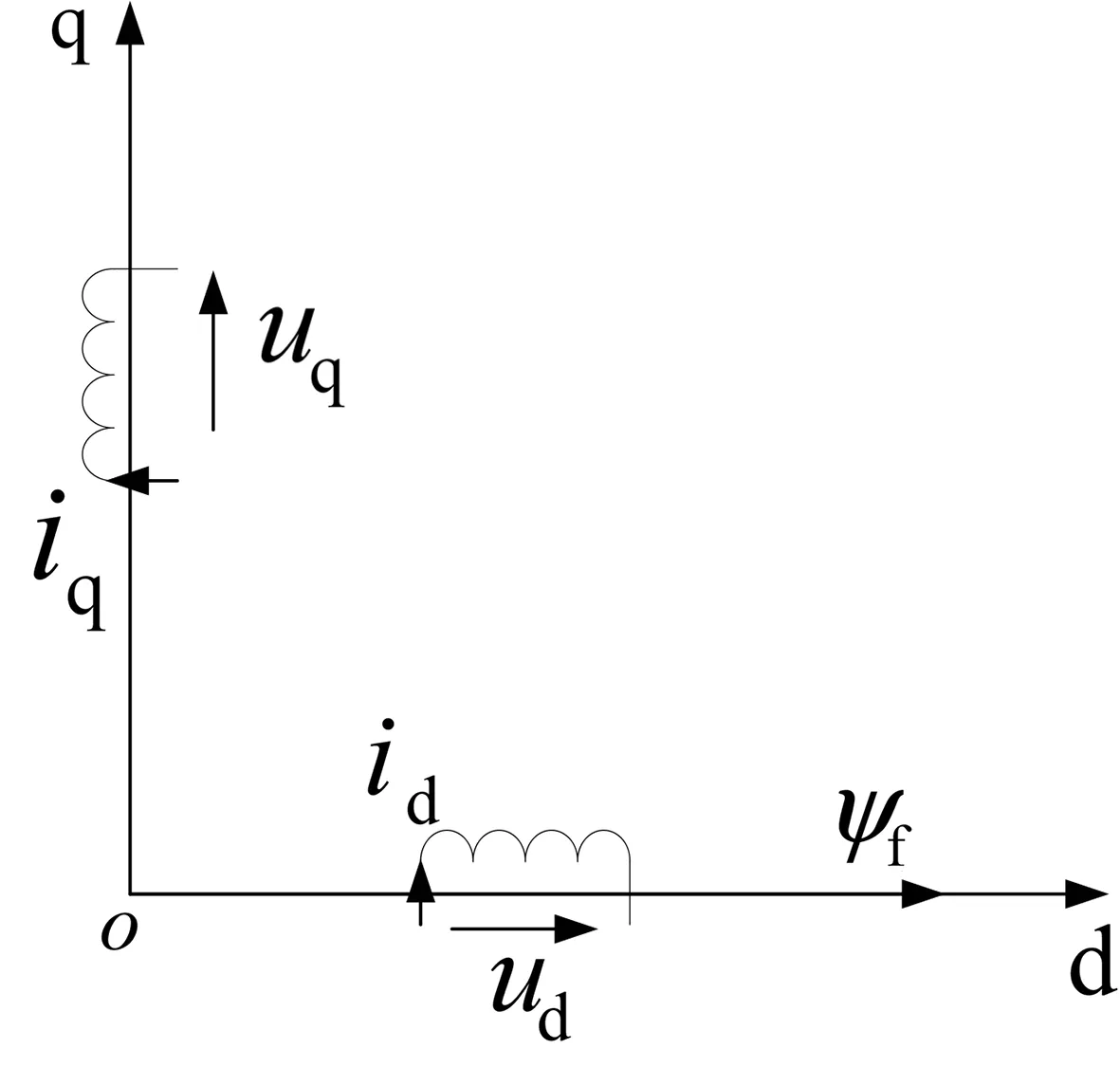
图3 永磁同步坐标系两相旋转坐标系Fig.3 Two-phase rotating coordinatesystem of PMSM

以转子的磁场方向为d轴(直轴)，以垂直于转子磁场的方向为q轴(交轴)，设为dq旋转坐标系。向量从静止两相坐标系转换到旋转两相坐标系的过程称之为PARK变换，其变换矩阵C2s/2r为

(9)

如图3所示，PARK后得到永磁同步电机两相旋转坐标系，此坐标系下推导电机数学模型[24-25]为

图中：ud、uq、id、iq分别为定子电压及电流矢量的两相旋转坐标系分量。

电压方程：

(10)

磁链方程：

(11)

转矩方程：

(12)

式中：ψd、ψq定子磁链d、q轴分量；Ld、Lq为定子电感及定子d、q轴等效电感；

2 直接转矩控制原理

直接转矩控制(DTC)最早出现于20世纪的80年代，与矢量控制不同，DTC直接将电机的磁链幅值和电磁转矩作为控制量。如图4所示，系统采集定子三相电压及电流信号经CLARKE变换后输入定子磁链及转矩估算模块，经计算后输出电磁转矩及磁链幅值信号作为反馈与参考值对比后输入Bang-Bang控制器。磁链扇区计算模块通过定子磁链ɑ、β轴分量确定磁链所在扇区。开关磁链选择模块获取两个bang-bang控制器及扇区计算模块信号后选择对应的空间电压矢量再发出六路脉冲信号控制逆变器的导通和关断[26]。

图4 直接转矩控制框图Fig.4 Direct torque control block diagram

2.1 磁链及转矩估算

DTC控制中，不需要确定转子的位置，因此可以将式(6)写为

(13)

由式(8)、(13)可估算出电机当前电磁转矩及磁链矢量。

2.2 扇区选择

图5 定子磁链扇区图 Fig.5 Stator flux sector map

如图5中所示，按照三相电机六个非零空间电压矢量的±30°方向将空间划分为S1、S2、S3、S4、S5、S6六个扇区。为确定定子磁链所在扇区，先计算三个磁链参考量ψref1、ψref2、ψref3。

(14)

当ψref1<0时计X=1，否则计X=0，同样将ψref2、ψref3和0比较得出Y和Z的值。再记N=4X+2Y+C。可以计算出每一个扇区对应的N值，得到表 1。

表1 磁链扇区N值对照表
Table1Nvaluecontroltableofmagneticchainsector

扇区(S)123456N315462

2.3 空间电压矢量策略

从式(13)中可知，磁链矢量的改变量Δψs是与空间电压矢量us的方向一致的。根据图5中的描述，当磁链处于不同扇区时，根据磁链幅值及电磁转矩的变化方向来确定所选的空间电压矢量，得到开关电压矢量选择表，见表 2。

表2 开关电压矢量选择表
Table2Switchvoltagevectorselectiontable

ΔψΔTeS1S2S3S4S5S6↑↑u2u3u4u5u6u1↑↓u6u1u2u3u4u5↓↑u3u4u5u6u1u2↓↓u5u6u1u2u3u4

2.4 MTPA算法

最大转矩比电流算法是在输出给定电磁转矩下，定子电流最小的控制方法。在dq坐标系上，定子电流满足：

(15)

(16)

联立(15)(16)式得

(17)

再将(17)代入(12)中得

(18)

3 系统仿真及分析

本系统所采用的IPMSM的参数为：Rs=0.64Ω、np=2、Ld=8.75mH、Lq=28.35mH，永磁体磁链ψf=0.1085Wb，转速给定为500r/min，给定的母线直流电压为100V。

图6 系统仿真图Fig.6 System simulation diagram

3.1 仿真结果及分析

系统仿真结果如下：

图7为电机负载启动转速曲线图。零时刻时电机还未启动，没有产生电磁转矩，电机在负载的作用下出现一小段负转速，在经过一段时间后，电磁转矩上升电机转速迅速上升，达到指定转速后逐渐稳定。图8为电磁转矩曲线，在电机启动后，转矩迅速上升至系统限制的最高值，在电机转速稳定之后，电磁转矩下降并与负载及阻尼转矩相平衡。图9为定子磁链变化曲线，在MTPA模块的作用下，磁链参考值是跟随转矩参考值变化而变化的。通过控制磁链的幅值来实现在不同转矩下定子交、直轴电流的最佳分配，使得定子电流幅值最小，提高电机效率。

图7 转速曲线Fig.7 Speed curve

图8 转矩曲线Fig.8 Torque curve

图9 定子磁链变化曲线Fig.9 Variation curve of stator flux

图10为基于MTPA算法的DTC控制电机定子三相电流曲线，图 11为在相同条件下设定磁链恒为0.6Wb时电机定子三相电流曲线。

图10 基于MTPA算法的三相电流曲线Fig.10 Three-phase current curve based on MTPA algorithm

图11 磁链恒定的三相电流曲线Fig.11 Three-phase current curve with constant flux

3.2 转矩脉动分析

图8中不难看出，电磁转矩的值始终不是固定的，而是在一定的范围内快速波动。这是由于传统的直接转矩控制中，bang-bang控制器只能输出高低两种信号，控制精度低，脉冲发生器在获取信号后所能选择的电压矢量有限，且在下以控制周期到来之前，所选的电压矢量将会作用于整个控制周期，作用时间也会随着电机运行状态的不同及滞环宽度的不同而发生变化，使得磁链和转矩在一个控制周期内会发生较大的变化，从而导致了电磁转矩的波动。

4 结论与展望

综上所述，结合车用永磁同步电机的特点在三种不同的坐标系下建立电机的数学模型，并基于DTC控制策在Simulink平台搭建电机闭环调速模型，分析了传统DTC控制策略低速转矩脉动的产生原因，采用MTPA算法优化车用永磁同步电机在低速恒转矩区的运行效率，并取得了一定的效果。但传统的直接转矩控制策略还需要进一步改进：

1)DTC控制策略由于bang-bang控制器的特点，在稳定运行时存在一定程度的转矩脉动；但当电机低速运转时，由于电机的磁链计算很大程度上会受到定子电阻的影响，因此定子电阻的变化和测量的不准确会进一步增加转矩脉动，影响到电机的低速运转性能，因此DTC控制策略低速定子电阻辨识和磁链估算策略还需要进一步研究改进。

2)传统DTC控制策略，开关频率不固定，降低效率的同时还影响开关件寿命，而随着近年来自适应变结构控制技术的发展和应用，在SVM-DTC的基础上结合滑模控制技术，大大提高了DTC控制系统的鲁棒性，降低了控制系统对电机参数的依赖，适用于车用永磁同步电机的高性能控制系统，具有较大潜力。