管道机器人跨井机构的设计与研究

，，，，

(南京理工大学机械工程学院，江苏 南京 210094)

0 引言

管道在腐蚀、重压等作用下会出现裂纹、漏孔等一系列现象[1]。同时，随着管道使用时间的增加，管道内壁会发生不同程度的结垢和杂质粘附，造成管道运输效率降低[2]。所以在使用过程中，管道需要定期进行检测、维修、清理，保证管道运输安全和效率[3]。但是，空间狭窄或内部环境恶劣的管道限制工作人员进入管道内部[4]。因此，管道机器人作为一种爬行设备逐步发展起来。管道机器人的发展为管道检测、维护提供了新的技术手段，极大提高了管道维护效率。

近年来，我国机器人技术取得了快速发展。典型的有螺旋式管道机器人、蠕动式管道机器人、伸缩式管道机器人、压差式管道机器人[5-8]。目前的管道机器人大多能顺利通过水平管道和一定倾斜程度的上升管道。但是在实际下水管道中，管道内部存在沉井，阻碍管道机器人在管道内连续行驶。当前还没有关于具有跨越沉井功能机器人的研究。针对上述问题，设计出一种能跨越沉井的管道机器人。

1 机器人跨越沉井的过程

管道机器人主要用于直径700 mm的管道，沉井两侧的管道在高度方向存在误差，机器人工作管道具体参数是：管道直径为700 mm；沉井直径为900 mm；高度误差为50 mm。

管道机器人采用分段式设计，分为车头、车身、车尾3个部分。机器人跨越沉井的过程相应的也分为3个阶段，车头、车身、车尾分别在3个阶段中依次通过沉井，图1是管道机器人通过沉井示意图。

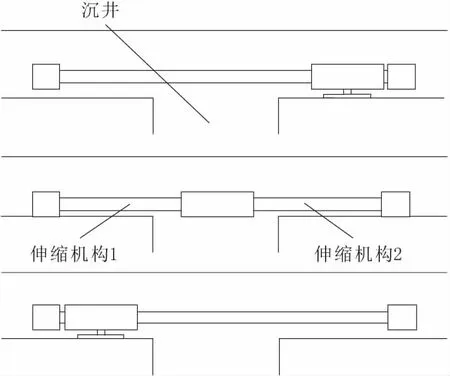
图1 管道机器人通过沉井

第1阶段，启动蜗轮蜗杆升降装置将机器人抬起一定高度。机器人上升到预定位置后，此时机器人车轮均处于悬空状态。机器人车身内部有两个相同的伸缩机构，分别和车头车尾连接。启动伸缩机构1，将机器人车头送至沉井对面。第2阶段，控制蜗轮蜗杆升降装置，让支撑装置恢复至初始位置，机器人车轮重新接触管道。在关闭伸缩机构1的同时开启伸缩机构2，通过交互利用两个伸缩机构，让机器人车身到达沉井对面。第3阶段，车身到达沉井对面后再次启动蜗轮蜗杆升降装置，让支撑装置将机器人重新上升到预定位置，机器人车轮再次悬空，关闭伸缩机构2，伸缩机构2回缩让车尾到达沉井对面。最后关闭蜗轮蜗杆升降装置，让支撑装置恢复至初始位置，管道机器人顺利通过沉井。通过3个阶段，机器人按照车头、车身、车尾的顺序依次通过沉井。

2 机器人升降机构的设计

图2是管道机器人升降机构机械结构图。上方是蜗轮蜗杆升降装置，电机驱动蜗杆，蜗杆带动蜗轮转动，蜗轮转动会让丝杠转动，实现上下移动目的。下方是支撑装置，跨越沉井时起到支撑作用。

蜗轮蜗杆升降装置的丝杠和支撑装置的连接杆间通过轴承连接，图3是丝杠和支撑装置连接示意图。通过轴承和方形连接杆限制作用，使支撑装置只能在预定轨道内上升和下降，避免支撑装置随丝杠转动与管道内壁发生接触。当支撑装置升降至预定位移后，因为蜗轮蜗杆的自锁功能可以使管道机器人停留在预定位置。

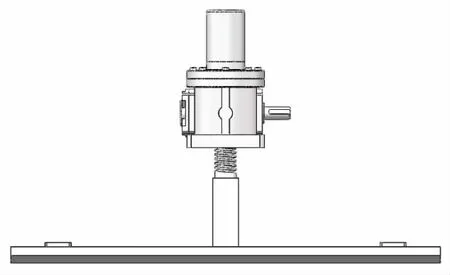
图2 升降机构机械结构

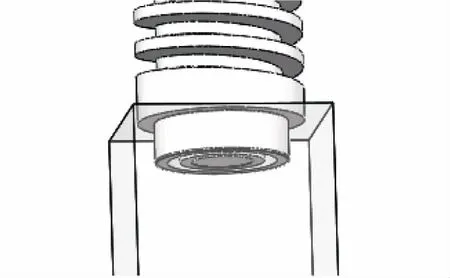
图3 丝杠和支撑装置连接

3 机器人跨越沉井的力学分析与仿真

3.1 机器人跨越沉井的应力分析

管道机器人在跨越沉井的3个阶段中，第1阶段和第3阶段都需要利用支撑装置，通过支撑装置，让车头和车尾能顺利通过沉井。为最大程度贴合管道内壁，支撑装置底面采用曲面板。2个阶段受力情况类似，以第1阶段为例，图4是第一阶段中支撑装置支撑面受力示意图。

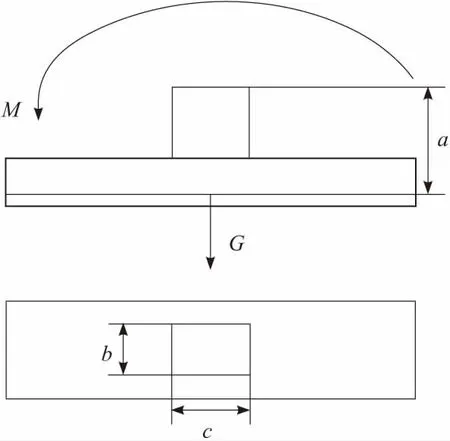
图4 支撑面受力

车头质量为m1，车身质量为m2，车尾质量为m3，重力加速度为g，单位长度的伸缩机构质量为m，伸缩机构的速度为v，工作时间为t，支撑底板厚度为a。根据力的平移定理，车头和伸缩机构分别都对支撑底面施加水平向下的力和逆时针方向的力偶。将两个力合并得到支撑装置承载区受到的合力G=m1g+m2g+m3g。车头产生的力偶M1=m1gvt，伸缩机构因伸长产生的力偶M2=0.5mgvt，2个力偶合成的总力偶M=m1gvt+0.5mgvt。总力偶M会对支撑装置连接杆造成倾覆作用，在力的作用效果上，可以通过水平向左的轴向力来代替。支撑底板受到竖直向下的合力G，因此，轴向应力σc为和正压力σp分别为：

(1)

圆柱曲板的轴压屈曲应力和圆柱曲板的外压屈曲应力分别为：

(2)

式中kc为圆柱曲板受轴压作用下的屈曲系数；ky为圆柱壳体受外压作用下的屈曲系数；E为弹性模量，单位是MPa；γc为弹性泊松比；a为曲板厚度，单位是mm；b为曲板较短边边长，即曲板的宽度,单位是mm；c为圆筒长度，单位是mm。

因此，圆柱曲板的轴向应力σc和圆柱曲板侧压应力σp必须满足σc<σcrc，σp<σcrp。

根据力的合成定理，轴向应力与正压力的合应力σ及合应力与水平方向夹角θ分别为：

(3)

从合应力σ可以得到：随着时间t增加，应力σ会随时间t增大，当车头达到沉井对面，即伸缩机构伸长到最大时，应力σ达到最大值，同时应力与水平方向夹角θ达到最小值。

3.2 机器人跨越沉井的应变分析

管道机器人跨越沉井时需要升高机器人，让机器人车轮和底盘离开管道。因为沉井两侧管道高度存在误差，尤其是沉井对面管道比机器人所在管道高时，必须通过控制升降机构伸长的长度保证机器人不与管道发生接触。机器人跨越沉井过程中，支撑装置连接杆因机器人重力影响会产生弹性变形，在跨越过程中机器人会和理想情况发生一定程度偏移，因此升降机构上升高度需要考虑支撑杆弹性变形的影响。在机器人跨越沉井第一阶段，因为支撑装置的支撑面与管道内壁紧密贴合，所以可以将连接杆底部视为与管道固连，支撑装置连接杆在第一阶段的受力如图5所示。

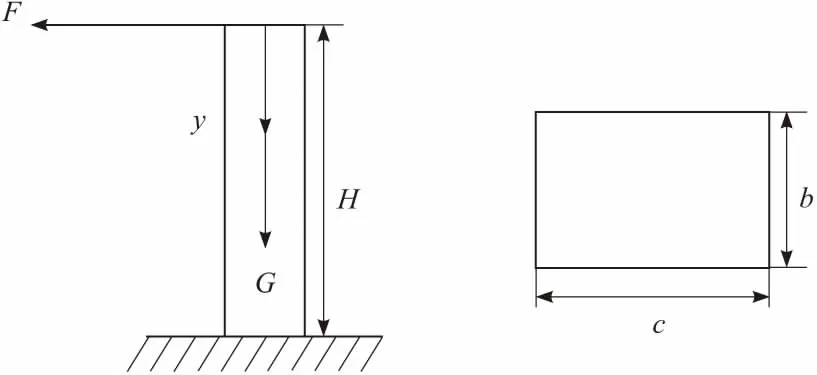
图5 连接杆受力

连接杆在竖直方向上的弹性变形量为：

(4)

E为弹性模量；b和c分别为连接杆横截面的长和宽，与前文出现的含义相同；H为升降机构伸长的长度。

连接杆顶部受到水平向左的力，连接杆会发生弯曲变形，连接杆向左移动的位移为δ，可以得到：

(5)

E为弹性模量；I为矩形截面对中性轴的惯性矩。

对式(5)进行两次积分，同时不考虑连接杆在竖直方向上的弹性形变，则当y=H时，连接杆的转角和位移均为0，将边界条件和惯性矩代入后可得连接杆的位移和转角方程为：

(6)

从式(6)可以得到，当y=0时，位移和转角最大，分别为：

(7)

正负号为位移和转角方向，F用式(1)表示。

因为连接杆弹性变形的原因，会导致机器人向下倾斜，车头底部在竖直方向上高度变化最大，图6是机器人跨越沉井第一阶段的位移变化图,图中l1为车头长度，l2为伸缩机构伸长后的长度，l3为车身的长度。因为车头高度h1必须大于沉井两侧在高度上的最大误差c，根据工作管道参数可知c=50 mm，最终推导得出升降机构理论最小伸长长度为：

(8)

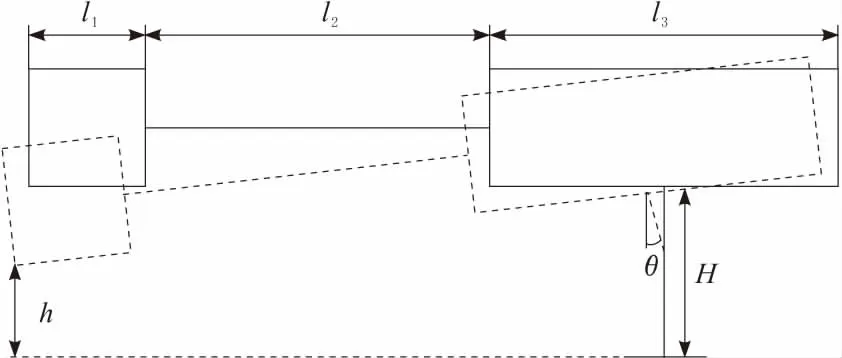
图6 机器人位移变化

3.3 基于ANSYS的仿真分析

为验证支撑装置受力情况，在ANSYS Workbench中对支撑装置进行应力应变分析。

根据管道机器人质量、电机转速、丝杠导程，设置底面为固定面，施加300 N压力和大小y=7.5×tN·m力偶，时间设置为30 s。图7～图10分别是10 s、20 s、30 s时支撑装置的等效应力图以及30 s时支撑装置的等效应变图。

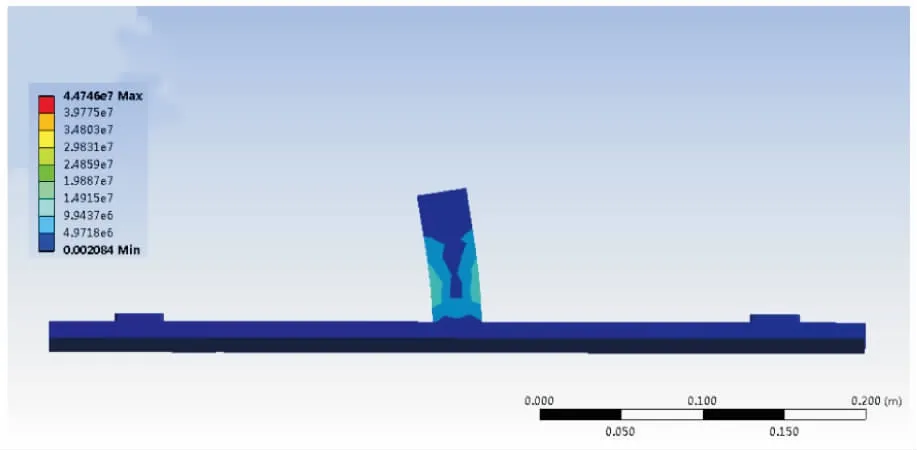
图7 10 s时支撑装置等效应力

图8 20 s时支撑装置等效应力

图9 30 s时支撑装置等效应力

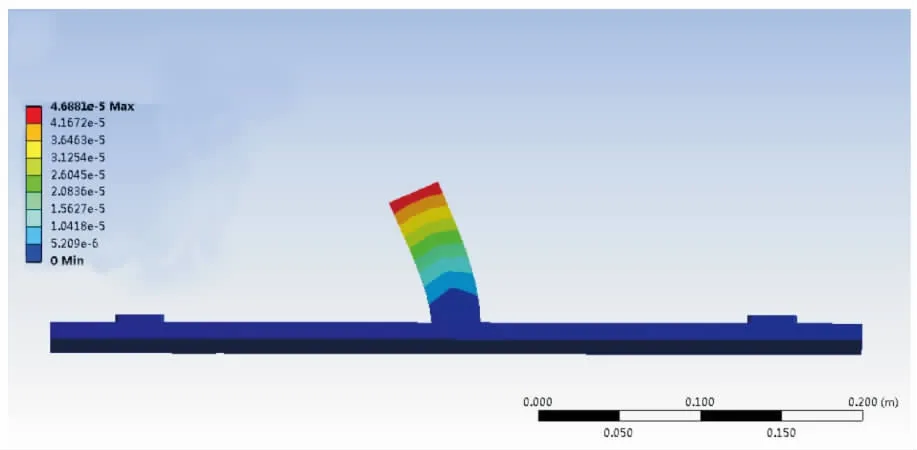
图10 30 s时支撑装置的等效应变

根据10 s、20 s、30 s时支撑装置等效应力图，能够得出应力随时间增大，并且30 s时有最大应力，最大应力为4.474 6×107Pa。同时在支撑装置受力过程中，每个阶段最大应力始终与水平方向呈现一定角度，且该夹角随时间而逐渐减小。

图10是30 s时支撑支撑装置应变图，最大应变发生在支撑杆最顶端，支撑装置的最大变形量为4.688 1×10-5m。根据支撑装置相关尺寸，求出理论最大位移δmax=3.472 2×10-5m。

理论值和仿真值接近。产生误差的原因在于H的实际值不等于50 mm，其值要大于50 mm。同时因为连接杆在竖直方向上也存在弹性变形，会对连接杆位移和转角造成影响，上述两点原因造成了理论值偏小，两者数据对比也进一步表明应力公式和升降机构理论最小伸长长度的合理性。

4 结束语

采用分段式设计方法，让机器能够按照车头、车身、车尾的顺序依次通过沉井。针对连接杆弹性变形问题，理论推导出连接杆应力方程和连接杆位移转角方程，并求解出最大位移和转角的表达式。根据最大位移和转角，进一步求解出升降机构理论最小伸长长度。利用ANSYS Workbench对支撑装置受力情况进行仿真，验证了应力公式的正确性，同时将最大位移的理论计算值和仿真结果值进行对比，并得出产生误差的原因，这为后续管道机器人样机开发和优化奠定基础。