管道机器人清淤装置设计与动力特性研究
,,,
(沈阳建筑大学机械工程学院,辽宁 沈阳 110168)
0 引言
城市管道的拥堵将直接导致城市排水困难进而引发内涝和污水溢出等许多影响生活和环境的重大问题[1-2]。目前的清淤方式有高压水枪法[2]、绞车法[3]、化学法[4]等;但上述清淤方法都有自身的局限性,而采用管道清淤机器人进行清淤可以克服上述不足,也是建设现代化城市和加强环保的需要,从而引起科研人员的广泛关注[5-6]。
目前,国内外对清淤装置的研究很少,缺少对管道复杂性的考虑,嵇鹏程[6]、崔曦元[7]、Nguyen[8]等设计的清淤装置可实现强力切削。上述清淤装置在一定程度上解决了管道清淤的一些问题;但其清淤装置简单,清淤功能单一,无法实现过载保护和管道自适应能力。因此设计了一种可以应用于复杂工况的清淤机器人,并对其清淤装置进行动力特性分析,用以研究其清淤作业的稳定性与可行性。
该清淤盘为旋转弹簧质量系统,对该系统进行动力特性研究。郝兵等利用特征线法对弹簧质量系统的动态响应进行了计算[9];陈强等为了分析移动载荷作用下梁的动态响应问题,建立了移动振动质量系统作用下梁的动力学模型[10];刘占芳等为探讨在离心振动复合环境下的动力学行为,建立了旋转系统的动力学方程[11]。对清淤装置进行了设计和基于旋转运动下的弹簧-质量系统的动力特性研究,结果表明,该装置满足清淤作业要求,运动稳定。
1 清淤装置及工作原理
1.1 清淤装置
管道清淤机器人由清淤部分、轮式行走部分、步进部分组成,如图1。轮式行走部分和步进部分属于前进部分,为清淤装置提供前进动力;清淤部分旋转运动进行清淤作业。该清淤装置由支撑装置和清淤盘组成,见图2。

图1 管道清淤器人整机结构
1.2 清淤装置工作原理
污泥的黏度随着搅拌转速的增大而快速降低,在搅拌转速达到20~100 r/min时污泥的黏度急剧下降达到平衡,污泥的黏度下降率达到94%,并趋于一个稳定值(极限黏度)[12]。依据该结论,确定清淤盘的转速为20~100 r/min。根据排污管道污水的流速范围,确定清淤装置前进方向的速度为0~2.5 m/s。表1为清淤机器人工作的实际工况参数。
清淤装置工作原理为:清淤盘随主轴一起沿着管道轴线转动,前进装置推动清淤装置沿着管道轴线平动,支撑装置承受来自清淤盘的径向和轴向力,如此清淤盘的合成运动为螺旋式前进运动,在该运动下清淤装置采取刮削—搅拌—过滤—推进—自流冲刷的清淤方式。在清淤过程中,刮刀将管壁上的附着物刮掉,并将污泥搅拌至推移状态;而后随着机器的前进和水流的作用使得满足直径的污泥颗粒可通过过滤网,而不满足的颗粒和杂物可由清淤盘推进到下一个检查井处为止,并通过吸污车等其他方式在检查井处取走污泥;过滤后的污水可通过排水管道的自流进行冲刷,将满足推移质的杂物冲走。
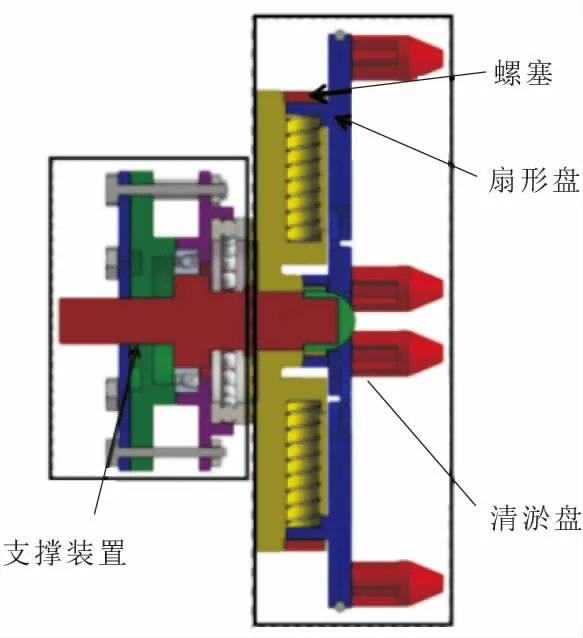
图2 清淤装置半剖图
该装置可获得高速和大推力的前进动力,具有复合式清淤功能,整体结构可实现管道自适应性和过载保护功能,可完成复杂的清淤任务。根据工况参数设定清淤装置的工作能力参数,见表2。

表1 清淤装置的工况参数
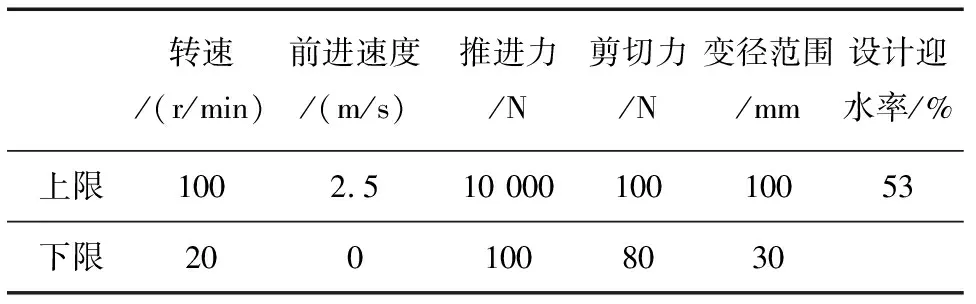
表2 清淤装置的工作能力参数
2 清淤盘运动分析
对清淤装置进行运动学分析,研究其清淤状态下的运动状态和过程,分析该运动对清淤作业的可行性,并通过运动仿真和曲线拟合确定扇形盘运动规律,为动力学分析提供参考。
2.1 运动学模型的建立
建立坐标系O-xyz,清淤盘的运动是沿着Oz的平动和绕着Oz的转动,运动简图如图3,其中r为扇形盘质心距旋转中心的距离。
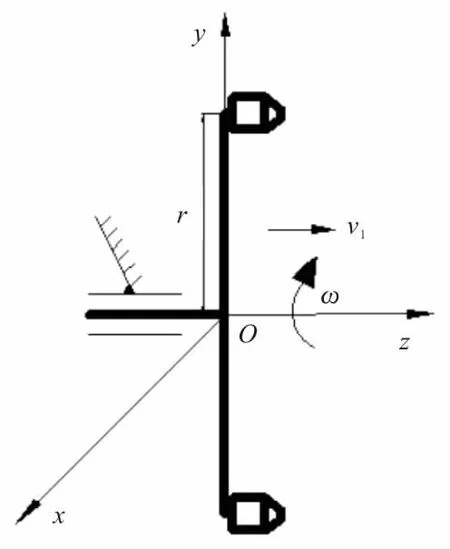
图3 清淤盘螺旋运动简图
在时间t内清淤盘沿着Oz平动位移矢量为S1,绕着Oz转动的位移矢量为S2。取一扇形盘作为研究对象,其在管道内的坐标矢量方程为:
S=S1+S2=Sx+Sy+Sz
(1)
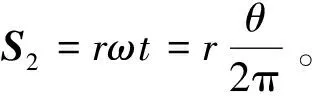
对(1)式进行矢量分解并转化为矩阵形式有:
(2)
螺旋运动的合成速度可表示为V=V1+V2=Vx+Vy+Vz,V2=ωt,有:
(3)
式(3)是清淤盘质心点的速度方程。
螺旋运动的合成加速度可表示为a=ax+ay+az,有:
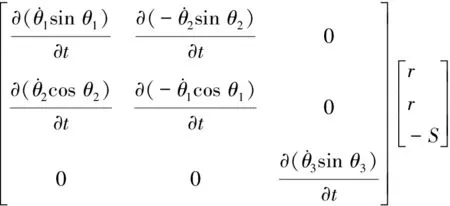
(4)
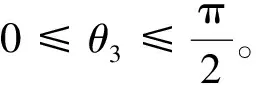
由此可根据清淤装置上任意一质点的初始位姿即可求得映射的位姿。
应用MATLAB软件对Sx的位移、速度和加速度的运动进行仿真,将其与下文中ADAMS软件的运动仿真曲线进行对比,以验证数学建模的正确性,拟合曲线如图4。
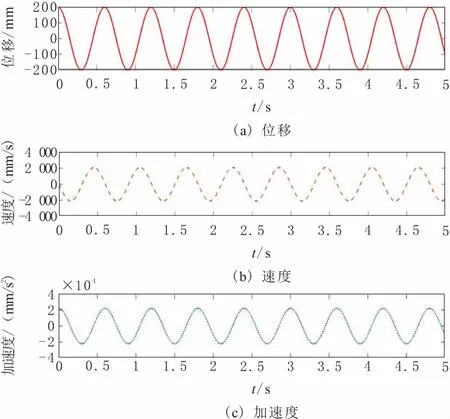
图4 扇形盘质心在Y方向的运动拟合曲线
2.2 运动学仿真分析
将三维模型导入到ADAMS当中,设置驱动,对清淤盘进行运动学仿真分析,仿真参数设置见表3,为了更清晰的表示真实情况下的运动状态,运动仿真考虑滑道内弹簧的作用,得到扇形盘质心的运动学仿真曲线如图5。

表3 清淤装置运动仿真设置

图5 扇形盘质心旋转仿真曲线

图6 扇形盘质心合成的运动曲线
仿真结果分析:
①由图4、图5,扇形盘质心基于MATLAB运动曲线与基于ADAMS的运动仿真曲线一致,验证了运动学数学建模的正确性。
②由图5,位移与速度曲线周期性均匀变化,而加速度呈周期性不规则变化,这是由于扇形盘与基盘滑道之间由弹簧支撑,仿真时考虑了真实状态下弹簧的作用,在运动过程中对加速度产生影响。
③如图6,位移呈线性增加,曲线平滑;速度围绕3.162 5 m/s呈周期性均匀波动,且在最高点和最低点处速度变化明显;加速度曲线贴近0 mm/s2不均匀波动。
运动学分析确定了扇形盘在管道内的运动为螺旋前进运动,清淤盘的运动状态平稳,满足四位一体清淤作业的运动要求。
3 清淤盘动力特性分析
清淤盘在实际工作中会受到自身重力、弹簧力、未知的惯性力和切削阻力的影响,所以为研究清淤盘实际工作的运动可行性和稳定性,从正、反两个方面对清淤盘进行动力特性研究,一是在主轴输入转矩的前提下得到清淤盘的运动状态和受力关系;二是在给定驱动的前提下得到运动状态和受力关系。在运动学的基础上,通过动力特性的研究可以更准确的分析运动与受力的关系,为电动机、弹簧的选取提供合理的依据,清淤盘动力学简图如图7。

图7 弹簧-质量动力系统简图
3.1 动力学建模
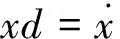
(5)
m为扇形清淤盘的质量;c为弹性系统阻尼,c=0;k为弹簧刚度系数,k=10 N/mm;F为弹簧弹力矢量,始终沿着滑道指向背离圆心方向;G为质点重力矢量,始终指向轴负方向;f为质点惯性力,f=mω2r,始终沿着滑道指向背离圆心方向;θ为旋转角度,设质心为A,则θ=∠AOx;200 mm≤x≤250 mm,200 mm≤y≤250 mm。
式(5)表示扇形盘在旋转时任意位姿的运动及受力状态。
3.2 清淤盘动力学正问题仿真分析
动力学正解分析即是在输入驱动力、阻力及弹簧预压力的条件下,研究清淤盘的运动状态和弹簧引起的碰撞力状态,进而判断其工作稳定性和可行性。对清淤盘进行动力学仿真,根据表2设置仿真参数,见表4。

表4 动力学仿真设置
仿真结果分析:
①由图8,运动状态与运动学仿真分析结果一致。
②由图9,碰撞力围绕25 N波动,随着转速的增加,碰撞力曲线会发生突变,最大碰撞力接近100 N。
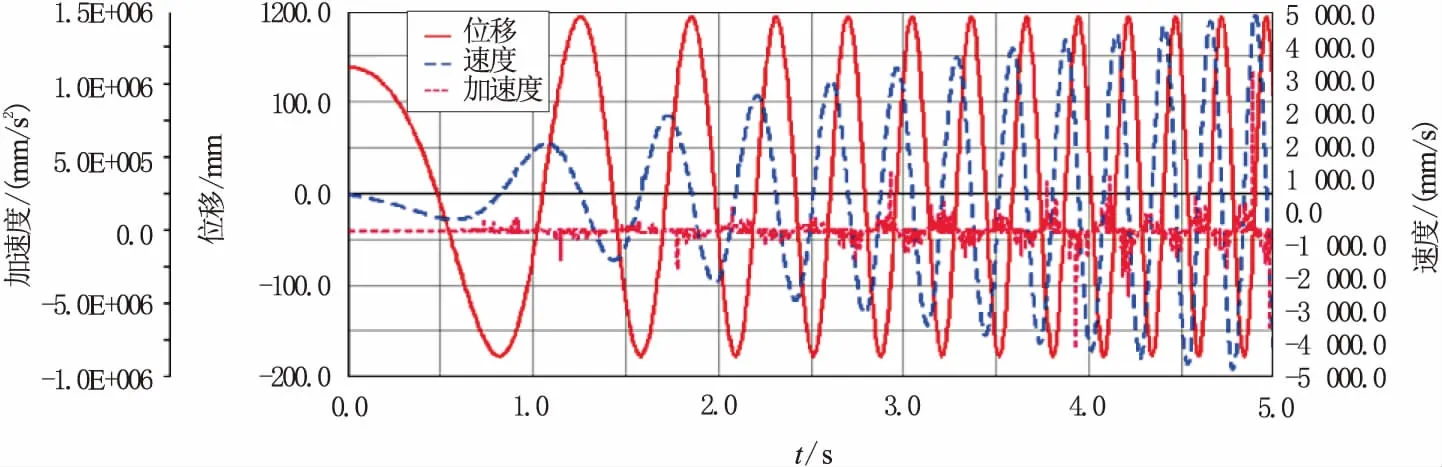
图8 扇形盘质心在Y方向的运动曲线
③由图10,在运动初期弹簧力有一瞬间达到了接近200 N,但运动稳定后弹簧力围绕35 N小幅度的变动;弹簧的变形有一瞬间接近15 mm,稳定后围绕0 mm小幅度波动。
动力学正问题分析确定了清淤盘的运动状态与运动学仿真一致,得到弹簧的受力与振动幅度和滑块的碰撞力的数值范围,为动力学逆问题研究提供参考。

图9 扇形盘与螺塞在Y方向的碰撞力及位移曲线

图10 弹簧受力及位移曲线
3.3 清淤盘动力学逆问题仿真分析
动力学逆解分析即是研究在输入确定的旋转速度,得到清淤盘的运动状态和主轴转矩,以及弹簧引起的碰撞力,用以验证该装置运动可行性,确定驱动电机的转矩。仿真设置驱动转速为100 r/min,推进速度2.5 m/s,阻力为0,其他设置同表4。仿真曲线如图11~图13。
仿真结果分析:
①由图11,滑块与螺塞的碰撞力围绕25 N周期性波动,最大值为65 N;滑块位移围绕0 mm上下波动,最大值为4.5 mm。
②由图12,弹簧位移围绕0 mm不均匀波动,最大值为5 mm;弹簧力围绕35 N不均匀波动,最大值为75 N。
③由图13,在阻力为0的前提下,为达到预设的转速,主轴转矩在0 N·m范围内不规则波动,最大值接近25 N·m。
动力学逆问题分析了在给定驱动时得到驱动所需的转矩,弹簧振动幅度与受力,以及碰撞力数值,与动力学正问题形成对比验证,说明弹簧的吸收能量的作用,其运动状态稳定,满足清淤作业运动要求,并为驱动电机和弹簧的选择和结构的强度校核提供参考。
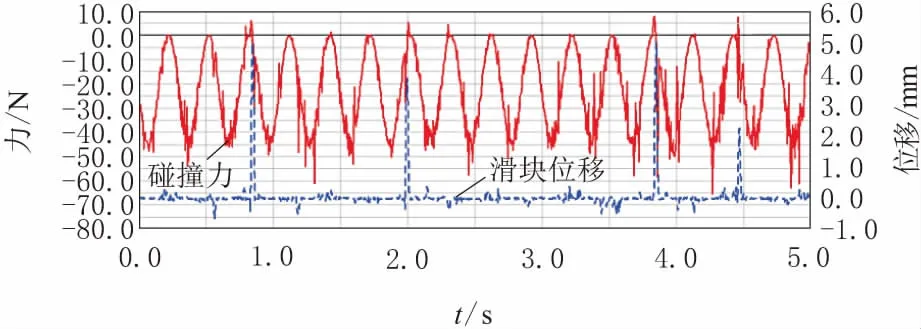
图11 扇形盘与螺塞在Y方向的碰撞力及位移曲线
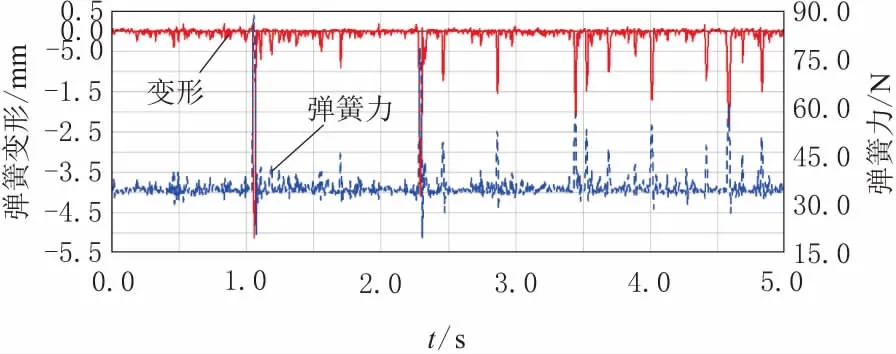
图12 弹簧受力及位移曲线
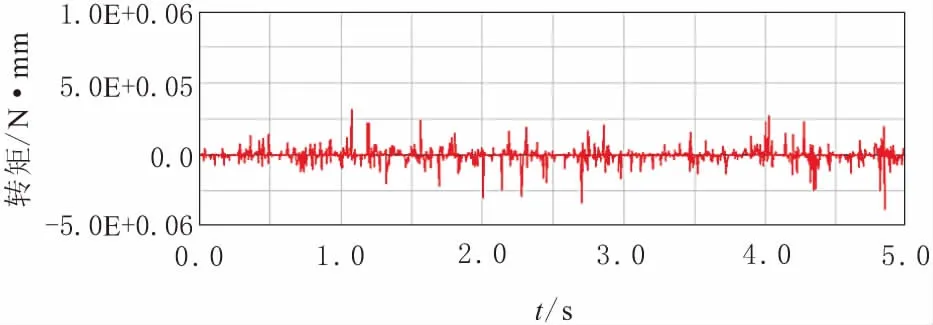
图13 驱动转矩曲线
4 结束语
基于SolidWorks和ADAMS建立了管道清淤装置的虚拟样机模型,对其进行机构原理和动力特性分析得出如下结论:
①清淤方式为刮削—搅拌—过滤—推进四位一体,清淤功能多样灵活,具有过载保护功能,可适应管道复杂的淤积工况,完成复杂清淤作业任务。
②动力学分析验证了清淤运动的合理性;弹性振动幅度小,曲线光滑运动平稳,对清淤作业没有影响;其动态特性良好,满足清淤装置清淤作业运动的可行性和稳定性,为管道清淤装置的深入研究提供参考。
———《扇形的认识》教学廖

