基于最优参数的改进Oustaloup滤波算法及其数字实现
,,
(1.中国电建集团华东勘测设计研究院有限公司,浙江 杭州 310014;2.杭州强夯基础工程有限公司,浙江 杭州 310014)
0 引言
分数阶微积分FOC(fractional order calculus)是求解任意阶次微、积分的一种数学方法,其为整数阶微积分的自然延伸。FOC理论的研究已有300多年的历史,早在 1695年 ,Hospital L与Leibnitz G W就对某个函数的分数阶导数问题进行过讨论[1]。由于当时FOC缺乏明确的物理意义及有效的数学工具,致使FOC理论发展较为缓慢,故在实际应用中大都采用整数阶的概念。直至1974年,在流变学、电化学、分形学及电力传输线理论等领域出现了FOC的应用背景,FOC理论才逐渐被国内外学者所重视。随着FOC数值算法的不断发展、各种分数阶控制系统的不断提出,更加推动了分数阶控制理论的发展,尤其是在20世纪末,FOC理论在控制系统中的应用已取得一些成果[2-5]。
FOC算子sα的数字实现是应用分数阶控制理论的基础,由于sα通常是复变量的无理函数,故其在实际应用中难以直接实现,此时需进行有理化近似,即采用高阶有理传递函数对上述无理函数进行逼近。目前,常见的有理近似方法有多种,比较有代表性有:CFE法、Carlson法、Chareff法、Matsuda法及Oustaloup滤波算法等,其中又以Oustaloup滤波算法应用最为广泛[2-3]。
标准Oustaloup滤波算法对FOC算子的幅频、相频特性具有很好的逼近效果,且拟合频率段范围较大,但其在拟合频率段端点附近的逼近效果相对较差。为改善上述缺陷,薛定宇等[4]对原算法进行了改进,提出一种改进Oustaloup滤波算法。分析上述算法可知,参数b与d的数值大小,将直接影响到改进Oustaloup滤波算法对分数阶微分算子sa的逼近精度,文献[4]已给出其推荐值(b=10,d=9),但它在拟合频域段[wl,wh]端点附近的拟合效果仍不够理想。鉴此,为进一步提高上述改进算法的逼近精度,利用文献[6]提出的改进自适应混沌粒子群优化算法(IACPSO算法)对参数b与d进行整定,进而使改进Oustaloup滤波算法在拟合频域段内达sa到实际幅频、相频特性的近似最优逼近。
1 标准Oustaloup滤波算法及其改进算法
1.1 标准Oustaloup滤波算法
标准Oustloup滤波算法采用有理函数级联的方式实现了对该无理函数的逼近,它的具体表达式为:
(1)
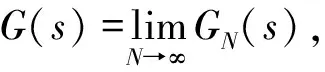
(2)
由式(1)可以看出,为实现对FOC算子sα的合理逼近,标准Oustaloup滤波算法需满足wμ=(wlwh)1/2=1的要求,即wlwh=1。
1.2 改进Oustaloup滤波算法
标准Oustaloup滤波算法对FOC算子的幅频、相频特性均有很好近似,且近似频率段的范围相对较大,但它在频率段端点附近逼近效果较差。为改善上述缺陷,文献[4]提出了一种改进Oustaloup滤波算法,其实质为在标准Oustaloup滤波算法前增加一个滤波器,它的具体表达式为:
sa≈Go(s)
(3)
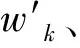
(4)
2 基于最优参数的改进Oustaloup滤波算法
2.1 目标函数的确定
为定量评价改进Oustaloup滤波算法对分数阶微分算子sα幅频、相频特性的逼近精度,分别对拟合频域段[wl,wh]内的频率与幅度绝对误差乘积积分以及频率与相位绝对误差乘积积分进行了定义,其计算公式分别为:
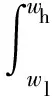
(5)
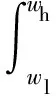
(6)
由式(5)与式(6)可知,ME与PE值越小,则说明改进Oustaloup滤波算法对sα幅频、相频特性的逼近精度越高。此外,为便于IACPSO算法对b与d进行参数寻优,将ME与PE的加权和作为参数b与d的优化目标函数,即:
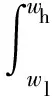
(7)
α1与α2为加权系数,用于调整幅频及相频特性近似的侧重,取α1=0.9,α2=0.1。
2.2 参数设置及寻优过程
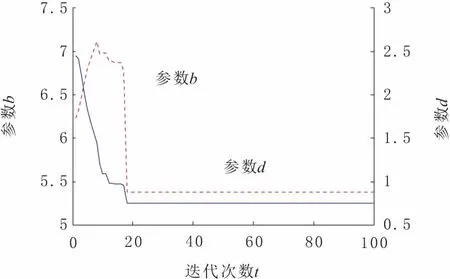
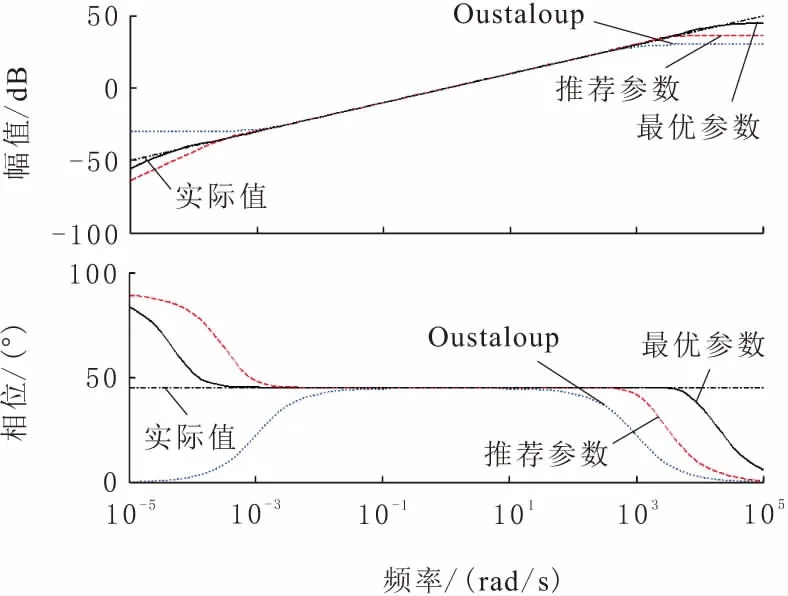
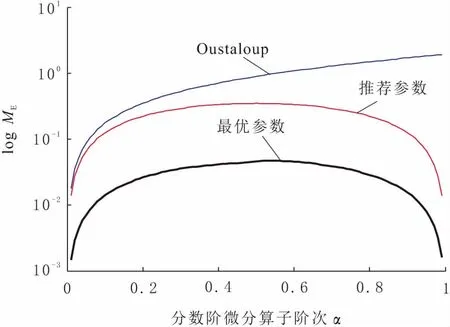
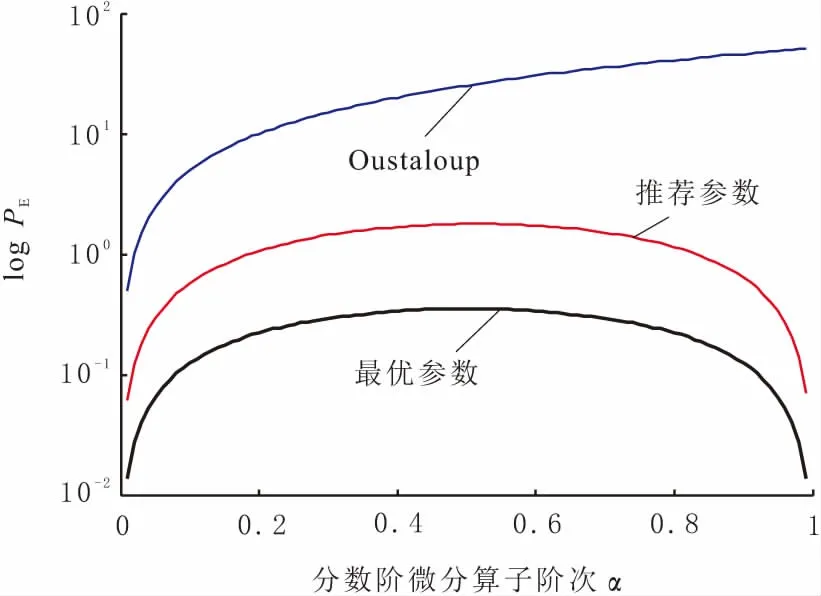
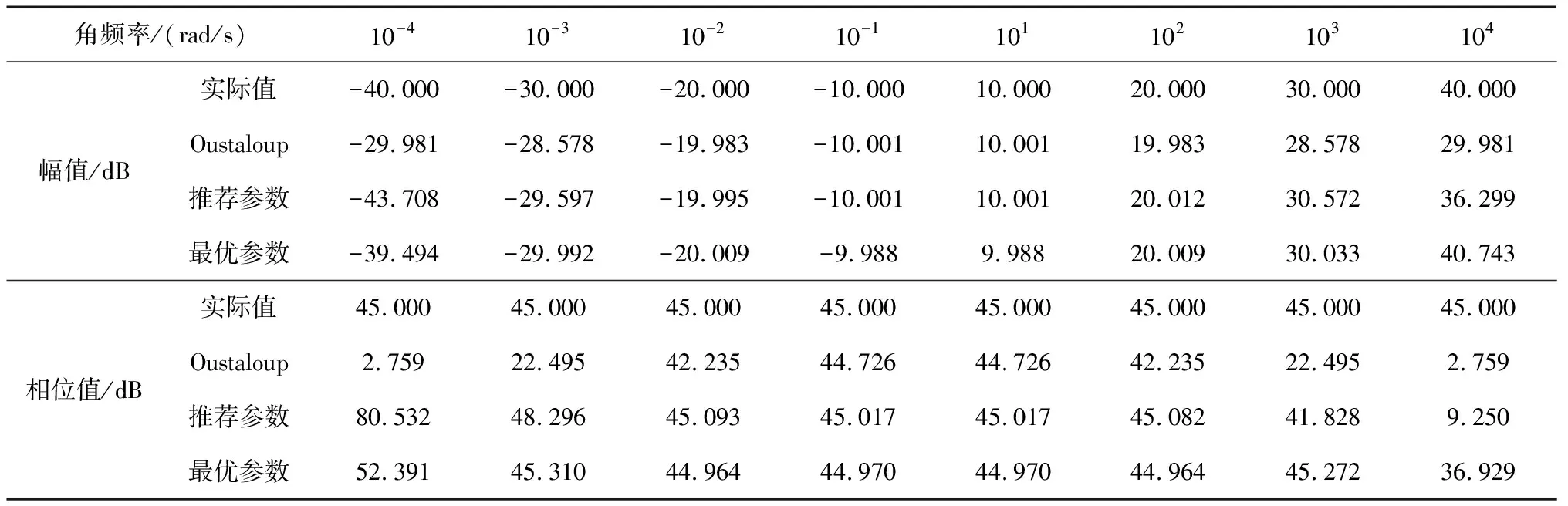
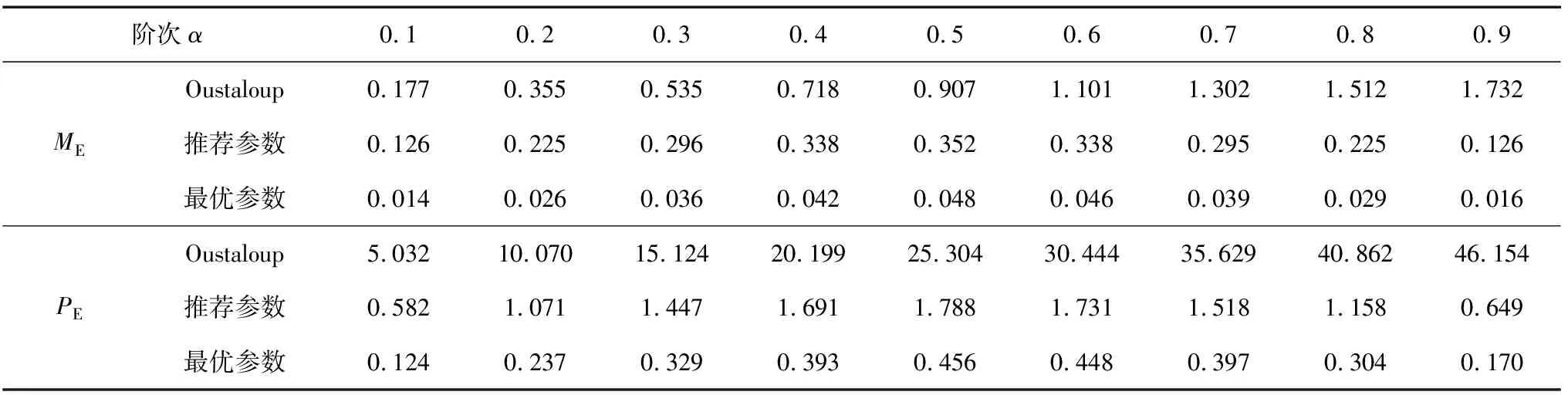
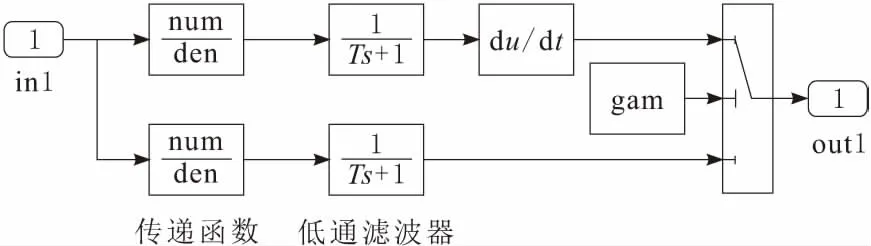
IACPSO算法的参数设置为:wmax=0.9,wmin=0.4,c1max=c2max=2.5,c1min=c2min=0.5,阈值δ=5,适应度阈值fδ=0.1,η1=0.5,η2=10 000,自适应调节系数β=0.5,混沌迭代次数Cmax=10,算法种群规模N=20,最大迭代次数Tmax=100;改进Oustaloup滤波算法的参数设置为:wl=10-3,wh=103,拟合阶次N=6,参数优化范围为0 为直观反映出改进Oustaloup滤波算法参数b与d的寻优过程,图1与图2分别示出了该过程的适应度值收敛曲线以及改进Oustaloup滤波算法最优参数的收敛曲线。由图1与图2可知,由于需确定的参数仅有2个,故IACPSO算法只经过20代左右的优化计算,b与d的参数寻优过程就已基本收敛,最终得到的最优参数为b=5.387 8,d=0.752 6,此时MPE=0.081 3。 图1 最优适应度值收敛曲线 图2 改进Oustaloup滤波算法参数的收敛曲线 为了验证基于最优参数(b=5.387 8,d=0.752 6)的改进Oustaloup滤波算法的有效性,利用该算法对分数阶微分算子sα(0<α<1)进行整数阶近似,并与标准Oustaloup滤波算法及基于推荐参数(b=10,d=9)的改进Oustaloup滤波算法进行对比,其中各算法的拟合阶次N=6,拟合频域段为[10-3,103]。上述各算法所对应的s0.5频域特性曲线如图3所示,表1给出了各算法下s0.5的幅值与相位值。 图3 分数阶微分算子s0.5的频域特性曲线 结合图3的幅频、相频特性曲线及表1中数据可知,在拟合频域段[10-3,103]端点附近,基于最优参数的改进Oustaloup滤波算法对s0.5的幅、频特性有最好的逼近效果,其次是基于推荐参数的改进Oustaloup滤波算法,标准Oustaloup滤波算法则逼近效果最差。以角频率等于10-3rad/s为例,在对s0.5幅频特性逼近方面,标准Oustaloup滤波算法与基于推荐参数的改进Oustaloup滤波算法所对应的幅值分别为-28.578 dB与-29.597 dB,其与实际值(-30 dB)的相对误差分别为4.740%与1.343%,而基于最优参数的改进Oustaloup滤波算法的相对误差仅为0.026 7%,较上述两种算法,分别下降了99.43%、98.01%;同时,在对s0.5相频特性逼近方面,标准Oustaloup滤波算法与基于推荐参数的改进Oustaloup滤波算法所对应的相位值分别为22.495 dB与48.296 dB,其与实际值(45 dB)的相对误差分别为50.01%、7.324%,而基于最优参数的改进Oustaloup滤波算法的相对误差仅为0.688 9%,较上述两种算法,则分别下降了98.62%、90.59%。综上可知,b取5.387 8、d取0.752 6对提升改进Oustaloup滤波算法在拟合频域段端点附近的逼近精度具有明显地促进作用。此外可见,基于最优参数的改进Oustaloup滤波算法的理想拟合频域段也得到较为明显的扩展,由原先设定的[10-3,103]扩展到[10-4,104]左右,这在某种程度上弥补了改进Oustaloup滤波算法仅在设定频域段具有较高逼近精度的不足。 为验证基于最优参数的改进Oustaloup滤波算法是否对任意阶次(0<α<1)的分数阶微分算子均具有更高的逼近精度,图4与图5分别示出了各算法所对应的ME,PE的对数值与分数阶微分算子阶次α的关系曲线,其中纵坐标分别为ME,PE的对数值。不同阶次下各算法对应的ME,PE值如表2所示,从表中可以看出最优参数。 图4 ME与分数阶微分算子阶次α的关系曲线 结合图4、图5及表2可知,随着阶次α由0增至1,标准Oustaloup滤波算法的ME,PE值均呈逐渐增大之趋势,而基于最优参数的改进Oustaloup滤波算法及基于推荐参数的改进Oustaloup滤波算法的ME,PE值则先增大后减小。此外可以看出,对(0,1)之间的任意阶次α,基于最优参数的改进Oustaloup滤波算法的ME,PE值均为三种算法中的最低值,以s0.1为例,其ME,PE值分别仅为0.014,0.124,较其它两种算法则分别降低了92.09%、63.28%及97.54%、78.69%,可见下降幅度非常明显,由此可说明,当wl=10-3,wh=103,拟合阶次N=6时,基于最优参数的改进Oustaloup滤波算法对任意阶次(0<α<1)的分数阶微分算子均具有更高的逼近精度,从而为间接实现分数阶PIλDμ控制器提供有力保证。 图5 PE与分数阶微分算子阶次α的关系曲线 表1 各算法下分数阶微分算子s0.5的幅值与相位值 表2 不同阶次下各算法对应的ME,PE值 为便于构建分数阶PIλDμ控制器的Simulink模型,分别对分数阶微分算子sα(0<α<2)及积分算子sβ(-2<β<0)设计了一个基于上述连续整数阶滤波器的Simulink自定义仿真模块。由式(3)可知,连续整数阶滤波器的分子与分母具有相同的阶次,该情况易造成Simulink在仿真过程中出现代数环(algebraic loop)现象,致使计算失效。鉴此,在该滤波器后面接一个带宽为10wh的低通滤波器以切断代数环,在不影响仿真模块计算精度的同时,尽可能地保证了计算稳定性。基于Simulink模块封装技术,构造出的分数阶微分算子sα(0<α<2)Simulink仿真模块的内部结构见图6。分数阶积分算子sβ(-2<β<0)Simulink仿真模块的内部结构见图7。 图6 分数阶微分算子sα(0<α<2)的 Simulink仿真模块 图7 分数阶积分算子sβ(-2<β<0)的 Simulink仿真模块 针对基于推荐参数(b=10,d=9)的改进Oustaloup滤波算法在拟合频域段端点附近对分数阶微分算子逼近精度较低的问题,提出了一种基于IACPSO算法的改进Oustaloup滤波算法参数优化方法,该方法将拟合频域段内的频率与幅度、相位绝对误差乘积积分的加权和作为优化目标函数,利用IACPSO算法对常数b与d进行参数寻优,经多次独立计算确定了一组最优参数(b=5.387 8,d=0.752 6)。与标准Oustaloup算法、基于推荐参数的改进Oustaloup算法的对比结果表明,基于最优参数的改进Oustaloup算法对任意阶次(0<α<1)的分数阶微分算子均具有更高的逼近精度,更宽的理想拟合频域段。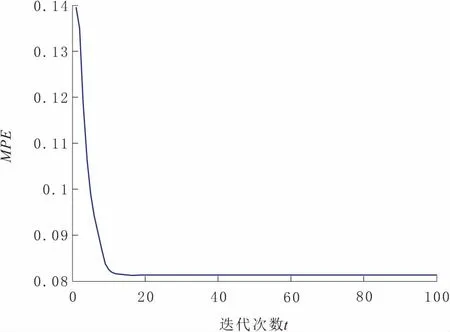
2.3 参数设置及寻优过程
3 FOC算子的Simulink自定义仿真模块


4 结束语

