热固耦合风力机齿轮传动结构的拓扑可靠性灵敏度分析

，， ，，

(1.沈阳工程学院新能源学院，辽宁 沈阳 110136；2.沈阳飞机工业(集团)有限公司，辽宁 沈阳 110034)

0 引言

双馈式风力机在运行过程中传动系统承受轴向力、径向力、剪切力、弯矩和扭矩等复合载荷的作用，通过拓扑分析风力机传动系统是一种涉及耦合场结构分析的重要应用性研究课题。增速箱齿轮运行啮合会产生包括热、声、电、磁、结构场等多种物理场，其中以温度、结构场对齿轮传动影响较大。传动系统运行热形成不均匀的环境温度场，其热量分布对增速齿轮系的承载能力、动态性能以及传动效率等有不同程度的影响，同时由于运行环境及轮系结构对齿轮传动系的运行载荷具有较强的交变影响，致使两种物理场耦合影响更加强烈，同时轮系中各齿轮固有频率与材料属性有直接的关联性，进而影响局部结构刚度的变化，并影响增速齿轮系的固有频率改变，易在齿轮箱正常运行时产生共振[1]。故在风力机传动系统机械可靠性优化设计中的共振——失效问题上，依据拓扑优化分析方法，可把握重要的可靠性设计要素，提高风力机传动系统的运行可靠性。

重点建立了热应力和结构应力耦合作用控制方程，采用节点位移为控制目标，从而分析影响齿轮系统运动振动机理。通过对比材料力学性能发生变化的影响和不均匀温度场热应力的影响下固有频率变化计算结果，基于随机结构的激振频率差绝对值，而设定稳定运行的阈值，建立传动齿轮系关系准则和随机结构振动可靠度准则；基于耦合场结构拓扑优化模型，运用Monte Carlo模拟法和有限元分析法相结合的概率分析法为手段，对齿轮系热固耦合场灵敏度进行分析。

1 热固耦合拓扑结构优化的理论基础

1.1 耦合场拓扑优化分析的材料插值模型

风力机传动齿轮系机械结构件本体的温度发生变化后，由于外部系统结构约束从而使内部各子部分之间造成热应力的产生[2]。对于风力机传动系统而言，传动系统的热膨胀、构件中的温度梯度和结构材料的各项异性是产生热应力的主要原因。具体到传动系统中齿轮箱的齿轮系的热应力是由于外部约束(螺栓预紧固定、齿轮支承轴承固定等)和内部约束(齿轮工作部分与非工作部分温度梯度、齿轮材料不同热膨胀系数)而造成。故耦合场拓扑优化分析的风力机增速箱齿轮系热弹性理论[3]可以表示为：

(1)

λ，G为拉梅系数；β为热应力系数；χe为相对密度；E，E0分别为优化后的相对弹性模量和单元初始结构刚度；p为惩罚权因子，以减少结构中间密度单元的数目，控制结构密度在0或1。其理论分析的前提是：①在离散单元内部的材料属性为常数，并且定义研究离散单元的相对密度；②单元材料属性，如杨氏模量和热传导率均随着单元相对密度的变化而变化，并且是与单元相对密度成指数变化关系，泊松比为常量。

1.2 耦合场的控制方程

以风力机传动系统热固耦合物理场作用下的拓扑优化设计问题为例。由于在热固耦合场中作用下风力机的传动结构几何非线性和材料非线性均很小，在实际问题分析可采用线性有限元分析方法。各向同性稳态热传导问题的有限元控制方程为：

(2)

在运行热作用的耦合场的结构控制方程为：

(3)

a为热传导系数；b1为对流换热而产生的单位体积热量；h为对流换热系数；t1为边界已知的热流量；u1为已知的温度向量；应力σij为温度场的函数；Dijkl为结构弹性矩阵；u2(i)为已知温度向量；t2(i)为已知外力矢量；εij为应变；σij为应力；ckl为热膨胀系数张量。

将温度场合和结构场有限元进行离散求解，热和结构系统分别可离散为2个有限元方程

R1=P1(x)-K1(x)U1(x)=0

(4)

R2(U1(x),x)=P2(U1(x),x)-K2(x)U2(x)=0

(5)

下标1表示温度场，下标2表示结构场，温度场导致结构热应变产生；K1为结构热传导矩阵；K2为结构刚度矩阵；U1为温度向量；U2为位移向量；P1为热载荷向量；P2为结构外载荷向量，系统矩阵和载荷向量是单元相对密度x的函数。

分别求解温度场合结构场后，进行耦合场构建建立拓扑结构模型，然后选用优化求解算法进行优化迭代求解。

1.3 耦合场的灵敏度分析

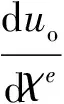
(6)

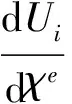
对体应力问题有

(-1 -1 1 -1 1 1 -1 1)T

(-1 -1 1 -1 1 1 -1 1)T

(7)

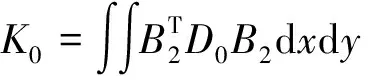
1.4 风电机组齿轮系热固耦合数值算法

风力机传动齿轮由于制造误差及材料本身的不均匀等随机因素，致使齿轮的固有频率具有不确定性，同时齿轮的固有频率随工作环境温度的变化而变化。在多种随机因素的复合作用下，增速箱齿轮的固有频率成为一个独立于传动系统的随机变量，结合干涉理论的可靠性研究，随机结构的失效状态函数方程为[4]：

gij=|pj-ωi|(i=1,2,...,n;j=1,2,...,m)

(8)

pj为齿轮运行环境下外载荷的第j个激励频率；ωi为齿轮第i阶固有频率。

对于增速箱齿轮结构发生共振，则齿轮处于失效状态。依据可靠性准则度量齿轮传动系统的随机结构为串联系统，其结构可靠度为：

(9)

1.5 概率有限元分析方法

ANSYS概率有限元法是将Monte Carlo法(又称为随机模拟法或统计试验法)与有限元结合，是基于有限元的概率的设计方法，以计算机为应用手段，通过对相关随机变量的抽样统计试验或随机模拟，从而估算和描述分析数据的统计量，对不确定因素对产品质量和性能的影响[5]，从而得到工程技术问题近似解的一种数值方法。结构函数为：

Z=g(x)=g(x1,x2,...,xn)

(10)

极限状态方程g(x1,x2,...,xn)将结构的变量总量为失效和可靠性两部分。由此产生n个基本变量的随机样本xj(j=1,2,...,n)，统计值落入失效域F={x:g(x)≤0}的样本点数为Nf，用失效的频率Nf/N替代失效概率Pf，可近似得出失效概率估计值为：

(11)

1.6 风力机耦合场拓扑优化计算流程

耦合场结构拓扑优化的计算流程一般为：

①定义材料常数、边界条件、载荷、工件刚度、设计域。

②离散设计域，初始化设计变量。

③分别求解热固耦合场问题的有限元方程。

④由伴随载荷方程求伴随矩阵向量，求结构响应的灵敏度。

⑤用基于Monte Carlo的概率有限元算法更新单元材料密度设计变量，进行材料优化分布计算。

2 三维数值算例

2.1 风力机齿轮实体模型的建立

以风力机传动系统中的相啮合齿轮副的某从动齿轮和轴为研究对象，齿轮参数如表1所示。齿轮的工作转矩为140 N·m，转速为3 150 r/min。

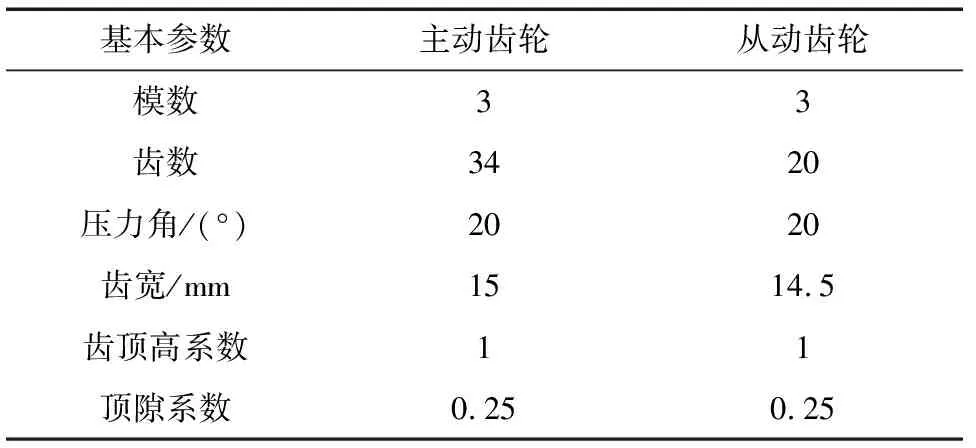
表1 齿轮参数

选用三维实体热分析单元Solid70，有限元模型计算域如图1所示。

图1 齿轮轴有限元分析模型

2.2 求解齿轮轴热应力

风电场风力机控制系统设定，当风力机齿轮箱运行温度为80 ℃时产生报警信号，当温度超过85 ℃时，发出停机指令。故依据风力机齿轮传动系统报警条件下设定风力机满载运行温度60 ℃，齿轮轴的热应力云图如图2所示。

图2 齿轮热应力云图

2.3 基于热分析的齿轮振动可靠性及灵敏度分析

基于机械原理经典理论，风力机传动齿轮的固有频率不仅与结构尺寸参数有关，且与齿轮工作条件下温度场有关，根据以上介绍的热固耦合计算方法，并采用概率有限元分析法进行基于温度场条件下齿轮机械可靠性及敏感度分析。

采用参数设计齿轮系结构参数，并且设为随机变量(参数服从正态分布)。各个随机变量的均值和标准差如表2所示。

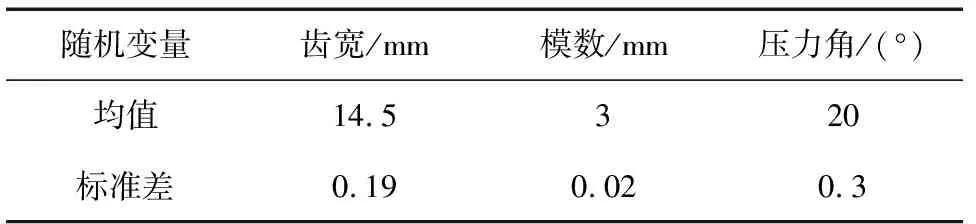
表2 齿轮各随机变量的均值和标准差

因固有频率跨度较大，利用ANSYS概率有限元法进行各随机样值1 000次的抽样，使得规定值更好的适应工程实际中的多个激励效果。由图3可以看出，随着抽样次数的增加，输出的均值和标准差曲线趋于水平，而且置信区间带宽较窄，精度满足工程需要。

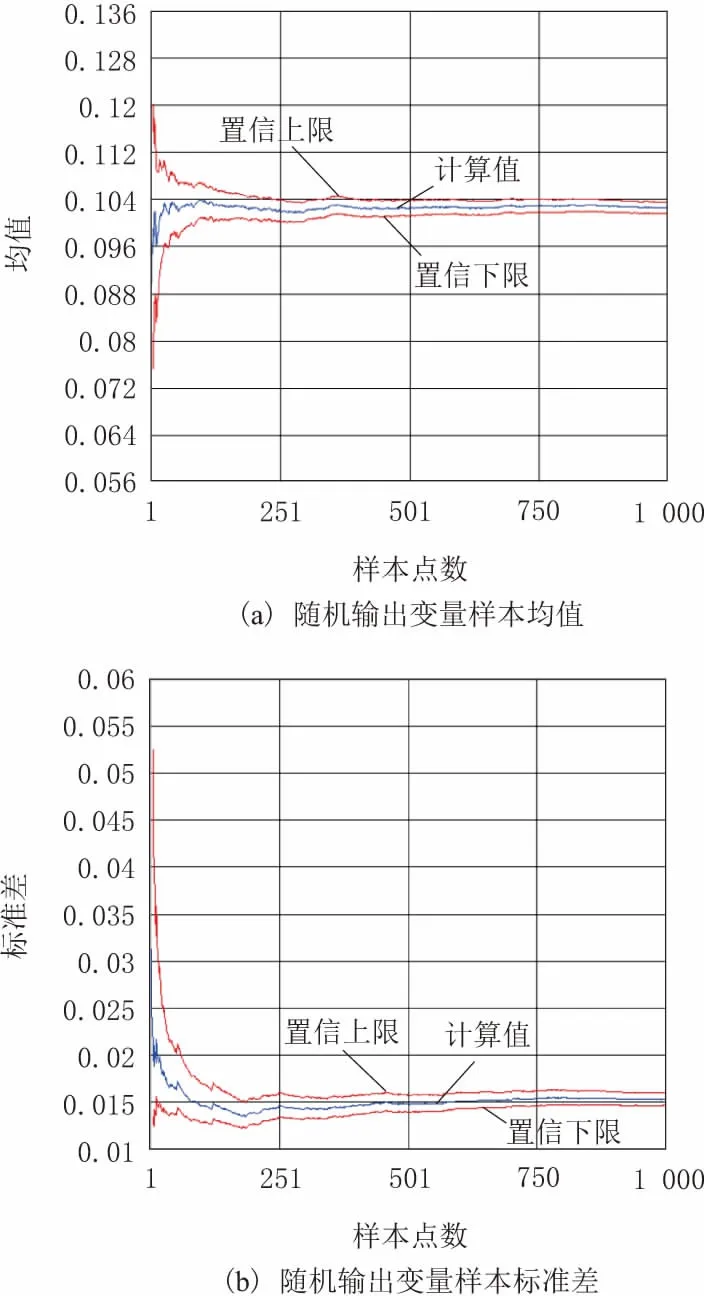
图3 输出变量的样本

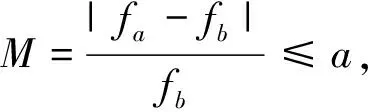
图4 基于拓扑分析法输出变量M的累积分布函数曲线

而仅基于概率有限元分析法得到的输出量的累计分布函数曲线入图5所示，其置信区间仅为0.65，由此可见，采用基于拓扑分析理论研究热固耦合风力机齿轮传动结构可靠性灵敏度与工程实际相吻合度更高。

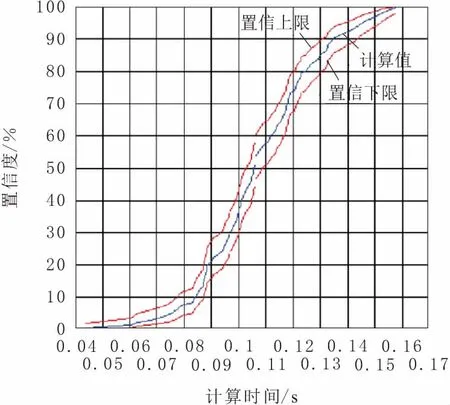
图5 仅基于概率有限元分析法得到的输出变量M的累积分布函数曲线

3 结束语

在温度场的影响下，风力机传动齿轮温度变化会直接影响整个传动系统的固有频率变化，而齿轮运行环境温度变化又使齿轮的力学性能改变，究其原因是由于风力机齿轮在工作过程中受到高速重载扭矩的影响，造成齿轮系内部热应力变化的结果，故加强风力机齿轮传动系统热分析设计是今后风力机可靠性设计必不可少的前提之一。

基于拓扑分析理论，通过重写温度场和结构场耦合方程，考虑材料力学性能和热应力发生变化影响综合因素下，由独立的热应力引起的固有频率变化低于由独立的材料力学性能变化对整个传动系统固有频率的影响，但热应力的存在进步增强材料力学性能对结构固有频率的影响。基于热固耦合场的风力机齿轮传动系可靠性设计，为提高风力机齿轮传动系统的可靠性提供重要的理论依据。

在考虑温度影响因素下，结合拓扑分析理论，采用ANSYS概率有限元方法引入到齿轮系的灵敏度可靠性分析中，分析结构灵敏度可靠性更高，置信区间更小，与齿轮随机参数中模数、齿宽、压力角变化对机械整体振动影响与工程实际应用更加吻合，故提高了可靠性分析结果的可信度。