正交各向异性锥壳外压临界失稳压力研究

胡嘉琦，贺小华，周昌玉

1 引言

金属钛有着密度小、比强度高、耐腐蚀性强等特点，广泛应用于压力容器。钛材在轧制过程中会出现织构现象，在轧制力作用下金属晶体会集体择优选择朝向，导致钛材各个方向的材料参数有显著不同，所以钛材是典型的正交各向异性材料[1-2]。目前，国内外标准[3-5]中将钛材视为各向同性材料进行处理，该处理方式虽便于工程应用，但会给压力容器设计带来一定的不确定性。

外压锥壳常用于航空航天、石油化工等领域，失稳是外压锥壳失效的主要形式。文献[6-7]对锥壳分别受轴压、外压和组合载荷作用下的屈曲失稳进行了实验研究，测得的实验值与理论公式计算值、标准解差异较大，由于有限元计算中考虑了实验结构的初始缺陷，所以计算结果与实验值较为接近。文献[8]采用有限元分析方法对斜锥壳及其等效正锥壳进行外压屈曲模拟计算，研究了两种锥壳在屈曲失稳模态形状的差异以及几何参数对临界失稳压力的影响。

文献[9]对正交各向异性薄壁圆筒临界失稳进行有限元分析，比较了有限元解与解析解、标准解的不同，讨论了材料不同卷板方式对临界失稳压力的影响，并对比分析了各向异性与各向同性外压圆筒的差异。圆筒和锥壳结构都是压力容器中常用结构，目前鲜有文献对正交各向异性锥壳外压失稳进行系统研究，关于正交各向异性和各向同性锥壳的差异性也未进行讨论分析。文献[10]依据Donnell理论，结合相关力学关系列出正交各向异性锥壳受外压时的平衡方程，并依据Galerkin&Ritz理论求解出正交各向异性变厚度锥壳临界失稳静压力和动压力计算公式。实际工程中，锥壳在制造过程中会造成结构缺陷，理论公式能否适用于实际工程中尚需进一步讨论。采用有限元分析法对正交各向异性锥壳进行外压失稳模拟计算，系统研究几何参数对临界失稳压力Pcr的影响，对比分析正交各向异性与各向同性锥壳的差异，讨论现行规范计算正交各向异性锥壳临界失稳压力方法的可行性。结果对进一步实现正交各向异性锥壳结构优化，有效提高承载能力具有重要意义。

2 外压锥壳有限元模拟

2.1 TA2正交各向异性材料参数

锥壳材料为工业纯钛TA2。通过实验测定TA2的材料参数[1]，实验数据，如表1所示。其中，x方向为板材轧制方向，y方向板材宽度方向，z为板材厚度方向。

表1 TA2材料参数Tab.1 Material Parameters of TA2

2.2 有限元计算模型

为了研究结构几何参数对正交各向异性锥壳临界失稳压力的影响，保持锥壳大端外直径DL不变，通过改变锥壳半顶角α以及径厚比来建立模型进行模拟分析。计算方案中DL=3000mm，径厚比 DL/T 值为 80、100、150、250，锥形比 λ（λ=1-Ds/DL）值为 0.35、0.5、0.65，半顶角 α 取值范围为（5～60）°，中间间隔 5°。采用shell181单元对模型进行网格划分，并进行网格无关性验证，shell181单元的有效可靠性在文献[2]中已有详细说明。

2.3 有限元模拟边界条件

参照文献[8，10]，锥壳大小端边界条件均采用简支约束，大小两端均约束环向位移，小端同时约束轴向位移，锥壳外表面施加压力。

2.4 有限元结构失稳分析方法

有限元失稳分析中，常使用特征值分析法和非线性分析法，但两种方法计算时常会得出相差较大的结果。为了验证两种方法的可靠性，选取文献[6-7]中锥壳外压实验模型，分别进行特征值分析和非线性分析，其中在非线性分析过程中采用“一致缺陷模态法”，施加实验模型的初始缺陷。分析所得的临界失稳压力，如表2所示。通过将两种方法的有限元计算结果与实验值对比可知，特征值分析结果与实验值相差较大，而非线性分析结果与实验值较为接近。由于考虑了模型的初始几何缺陷以及几何大变形等因素，故采用有限元非线性分析求解的临界失稳压力较为准确。

表2 不同分析方法得到的临界失稳压力Tab.2 The Critical Buckling Pressure Calculated by Different Methods

3 外压锥壳临界失稳压力研究

锥壳在设备中常起连接作用，主要的连接形式有圆筒—锥壳—圆筒。当上下所连接圆筒直径与厚度都确定时，在满足工程使用条件下，只能通过变化锥壳半顶角来改变壳体结构。

选取锥形比λ=0.5的锥壳为研究对象，利用非线性分析法研究不同几何参数下正交各向异性锥壳临界失稳压力。模拟过程中将标准[3]所规定的最大允许偏差作为模型的初始几何缺陷施加。模拟所得临界失稳压力Pcr，如图1（a）所示。

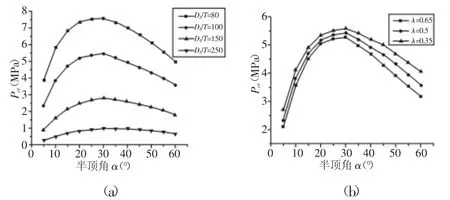
图1 正交各向异性锥壳临界失稳压力Fig.1 The Critical Buckling Pressure of Orthotropic Conical Shell

从图中可知，随着锥壳半顶角的增大，Pcr先增大后逐渐减小。分析认为，在其他结构参数不变时，锥壳轴向长度的缩短对锥壳临界失稳压力Pcr有着两种不同的作用。一方面，随着锥壳轴向长度的缩短，锥壳受大小端支撑线的边缘效应作用逐渐加强，有助提高外压稳定性；另一方面，随着锥壳半顶角α的增大，对锥壳外压稳定性有抑制作用，与文献[8]结论一致。

综合考虑锥壳大小端增强影响和锥壳半顶角大小等因素，可有效提高锥壳的抗失稳能力。从图中可得，不同径厚比的锥壳结构，在半顶角从（5～60）°的变化过程中，Pcr最大值与最小值的比值可达到（1.9～3.6）。锥壳在半顶角30°附近的抗失稳能力最强。对于单一使用的锥壳，还可通过改变径厚比有效提高锥壳抗失稳能力。

为验证上述规律的一般性，选取径厚比DL/T=100，锥形比λ为0.35、0.6的锥壳进行模拟计算，模拟结果，如图1（b）所示。从图中可得，不同锥形比的锥壳，其中，Pcr随半顶角的变化规律基本相同。由此说明，一定锥形比及径厚比下，在半顶角30°附近，锥壳抗外压失稳能力最强。

4 外压锥壳临界失稳压力的比较

4.1 正交各向异性锥壳临界失稳压力与理论公式计算结果比较

文献[10]推导出简支条件下正交各向异性锥壳外压临界失稳静压力公式：

式中：Eθ、Et—锥壳环向和母线方向上的弹性模量；vtθ、vθt—泊松比；r2—闭合锥壳母线长度；γ—锥壳半顶角；b1、b2、b3、b5、b6—相关系数，详见文献。

利用式（1）分别计算不同几何参数的锥壳临界失稳压力Pcr，选取锥形比λ=0.5的锥壳为例，理论公式与有限元计算结果，如图2所示。从图中可知，径厚比较小时，相同参数下，Pcr解析解远大于有限元解。解析解的变化规律与有限元解较为相似，随着锥壳半顶角的增大，Pcr先增大后逐渐减小。解析解与有限元解达到最大值时半顶角范围存在差异，解析解在半顶角40°附近时最大，而有限元解则在半顶角30°附近时达到最大值。

为了进一步分析解析解与有限元解的差异性，以及讨论理论公式在工程设计中的适用性，正交各向异性临界失稳压力Pcr有限元解与解析解比值，如图2所示。P1为有限元解，P2为解析解。从图中可知，随着锥壳半顶角的增大，P1/P2值逐渐减小而后趋于一定值。不同锥形比下，P1/P2变化规律基本一致。由于理论公式解适用于薄壳且未考虑缺陷，径厚比较大时，有限元解与解析解较为一致，径厚比较小时，有限元解与解析解差异较大。

由图 2可知，不同锥形比下，在半顶角（20～45）°范围内，当径厚比DL/T≥150时，P1/P2值范围为（0.8～1.2），Pcr解析解与有限元解具有较好的一致性，可适用于工程设计中。

图2 正交各向异性锥壳临界失稳压力有限元解与解析解比Fig.2 The Ratio of Critical Buckling Pressure Between Finite Element Solution and Analytical Solution

4.2 正交各向异性与各向同性锥壳临界失稳压力的比较

标准[3-5]中将钛材视为各向同性材料，其应力—应变曲线是按钛材轧制方向拉伸绘制的，泊松比取0.32。为比较正交各向异性与各向同性锥壳之间的差异，各向同性锥壳临界失稳压力模拟计算中，材料参数取板材轧制方向数值。选取锥形比λ=0.5的锥壳为例，各向同性与正交各向异性锥壳临界失稳压力Pcr，如图3所示。从图3中可知，正交各向异性性锥壳临界失稳压力变化规律与各向同性锥壳基本相同，相同参数下，正交各向异性锥壳临界失稳压力值均大于各向同性锥壳。

图3 正交各向异性与各向同性锥壳失稳压力Fig.3 The Critical Buckling Pressure of Orthotropic Conical Shell and Isotropic One

为了进一步分析正交各向异性与各向同性锥壳的差异性，正交各向异性与各向同性锥壳临界失稳压力的比值，如图4所示。图中：P3—各向同性锥壳临界失稳压力。从图中可知，随着锥壳半顶角、径厚比和锥形比的增大，P1/P3值逐渐减小，但减小的幅度都不大，相同参数下，正交各向异性锥壳临界失稳压力值普遍高于各向同性锥壳（15～23）%。由于正交各向异性材料的力学参数和本构关系与各向同性材料有一定的差异，使得两者之间的抗弯模量和抗扭刚度有所不同，导致两者的抗失稳能力也不同，正交各向异性锥壳的抗失稳能力要强于各向同性锥壳。

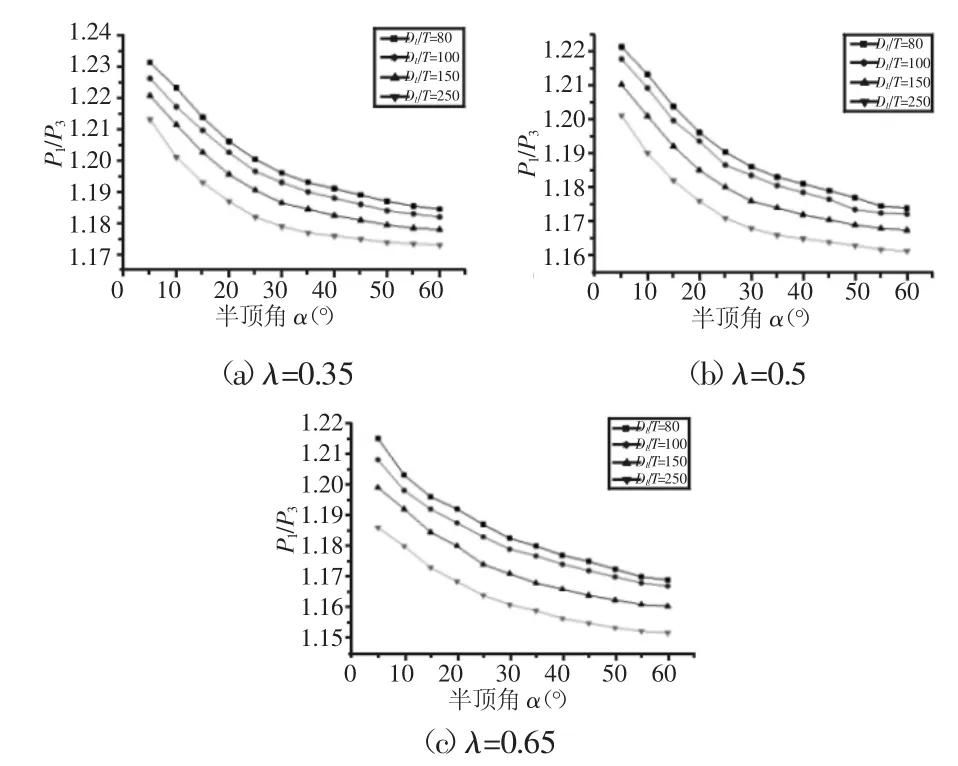
图4 正交各向异性与各向同性锥壳临界失稳压力比Fig.4 The Ratio of Critical Buckling Pressure Between the Orthotropic Conical Shell and Isotropic One

4.3 正交各向异性锥壳与等效各向同性圆筒临界失稳压力的比较

锥壳外压失稳问题相对比较复杂，相关实验研究表明，锥壳失稳过程与等效圆筒失稳过程相似，所以标准中将锥壳等效成圆筒进行设计。标准[3，5]中采用等效方法处理锥壳稳定性问题，其等效圆筒直径d=（DL+Ds）/（2cosα），等效圆筒长度为锥壳母线长度L，等效圆筒厚度为锥壳厚度T。由于现行设计标准中将钛材视为各向同性材料，故正交各向异性锥壳被等效成各向同性圆筒进行设计，为了比较分析两者之间的差异性，将不同几何参数的正交各向异性锥壳等效成各向同性圆筒，模拟计算其临界失稳压力，圆筒的边界约束条件与锥壳相同，计算过程中模型施加等量的初始几何缺陷。选取锥形比λ=0.5的锥壳为例，等效各向同性圆筒与锥壳临界失稳压力Pcr，如图5所示。从图中可知，正交各向异性锥壳临界失稳压力变化规律与等效各向同性圆筒基本相同，相同参数下，正交各向异性锥壳临界失稳压力值均大于等效各向同性圆筒。

图5 正交各向异性锥壳与等效各向同性圆筒临界失稳压力Fig.5 The Critical Buckling Pressure of Orthotropic Conical Shell and Equivalent Isotropic Cylinder

为了进一步分析正交各向异性锥壳与等效各向同性圆筒的差异性，正交各向异性锥壳与等效各向同性圆筒的临界失稳压力比，如图6所示。图中：P4为等效各向同性圆筒临界失稳压力。从图中可知，随着半顶角的增大，P1/P4值不断减小，正交各向异性锥壳临界失稳压力值与等效各向同性圆筒差异逐渐减小。随着锥形比的增大，正交各向异性锥壳临界失稳压力值与等效各向同性圆筒差异逐渐增大。

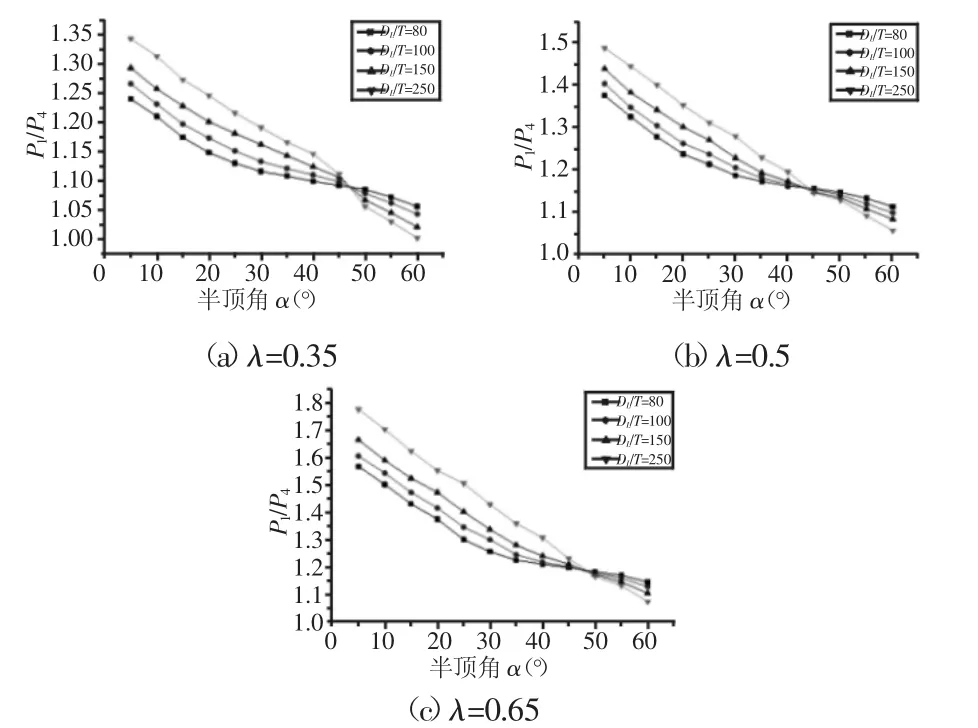
图6 正交各向异性锥壳与等效各向同性圆筒临界失稳压力比Fig.6 The Ratio of Critical Buckling Pressure Between Orthotropic Conical Shell and Equivalent Isotropic Cylinder

工程设计中，正交各向异性锥壳等效成各向同性圆筒具有保守性。当锥壳半顶角较小时，正交各向异性锥壳等效成各向同性圆筒具有较高的安全富裕量；当锥壳半顶角较大时，正交各向异性锥壳等效成各向同性圆筒安全富裕量适可。

5 结论

利用有限元非线性分析法，对不同几何参数的正交各向异性锥壳临界失稳压力进行系统研究，模拟计算结果与理论公式、各向同性锥壳以及等效圆筒进行比较，得到以下结论：

（1）在其他几何参数不变的情况下，随着锥壳半顶角的增大，正交各向异性锥壳临界失稳压力先增大后逐渐减小，半顶角在30°附近，锥壳外压抗失稳能力最强。

（2）锥壳径厚比较大时，解析解与有限元解有较好的一致性，锥壳在半顶角（20～45）°范围内，当径厚比 DL/T≥150 时，解析解可适用于工程设计中。

（3）正交各向异性锥壳临界失稳压力值普遍高于各向同性锥壳（15～23）%。

（4）正交各向异性锥壳等效成各向同性圆筒具有保守性。当锥壳半顶角较小时，正交各向异性锥壳等效成各向同性圆筒具有较高的安全裕量；当锥壳半顶角较大时，正交各向异性锥壳等效成各向同性圆筒安全裕量适可。