自堆式螺旋滚动导轨的结构分析与建模
鄢正清,武 凯,宋 坤,孙 宇
(南京理工大学 机械工程学院,江苏 南京 210094)
1 引言
自堆式螺旋速冻机以其生产效率高、自动化程度高、占地面积小、卫生条件好等优点引领了未来新型食品速冻装备的发展趋势,目前众多速冻食品进口国专门要求进口的速冻食品必须从这类自堆式螺旋速冻装置加工生产。我国作为速冻食品的出口大国,研究自堆式螺旋速冻机对于促进我国速冻食品工业的快速健康发展具有重要意义。
在螺旋自堆式机械系统中,螺旋滚动导轨对于螺旋塔的支撑和传动起着重要作用,是自堆式螺旋速冻机的重要功能部件。在螺旋塔堆叠区,两根同心的环形驱动链条分别定位在架空的两根同心螺旋线轨道上,并在轨道上运行,该螺旋轨道具有一定的升角并只有一个导程,使驱动链条形成一个导程的螺旋线轨迹。螺旋滚动导轨作为重要的传动部件与支撑部件,其结构布局对于自堆积螺旋塔的稳定形成和结构紧凑性有重要作用,其性能极大地影响着自堆式螺旋速冻机的运行速度、运行稳定性和噪声控制。接触刚度作为螺旋滚动导轨的性能指标之一,具有重要的研究意义。
2 螺旋滚动导轨的结构布局
内、外侧螺旋滚动导轨示意图,如图1所示。在外侧导轨中,驱动轮侧水平于地面且高度与交叉处A点的高度相同,AM、、NN′段水平于地面,AA′的垂直距离为h+Δh,式中:h—输送
带支撑挡边的高度;Δh—防止干涉的间隙;从动轮与水平面呈一定夹角γ,ON′、PA′段靠近从动轮部分平行于从动轮,并通过弧线分别与负载段和驱动段平缓衔接;图中C点和Q点为驱动链条负载段和驱动段脱离重合的点,张紧导向导轨的安装长度为L。
由于驱动段驱动部分和从动部分衔接处的弧线平缓,故将其近似为直线,于是从动轮与水平面所呈夹角γ与驱动链条位置满足关系:

考虑到输送带自堆积的顺利驱动与链条的合理布置,应满足:

考虑到驱动链条位置结构的紧凑性,应满足:
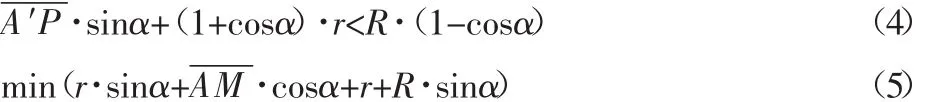

图1 内、外侧螺旋滚动导轨示意图Fig.1 The Diagram of Inner and Outer Spiral Rolling Guide
在内侧导轨中,驱动轮侧水平于地面且高度与交叉处G点的高度相同,E′E、ED、DG段水平于地面,GG′的垂直距离为h+Δh;从动轮与水平面夹角为,IH、JE′段靠近从动轮部分平行于从动轮,并通过弧线分别与负载段和驱动段平缓衔接;图中:F点—驱动链条负载段和驱动段脱离重合的点。
与外侧驱动链条位置不同,内侧驱动链条驱动段的驱动侧和从动侧在螺旋塔内不会占据额外的位置,因此它只需满足:

其中:JE′>L,I H>L,θ—螺旋导轨的螺旋升角。
3 螺旋导轨系统的力学模型分析
在螺旋滚动导轨系统中,滚珠同驱动链条和轨道的沟槽同时接触,在外载荷的作用下导轨和驱动链条的弹性变形相对滚珠的弹性变形较小,因此只考虑滚动体的弹性变形[2]。螺旋滚动导轨所在圆周直径远远大于其导程和轨道横截面尺寸,为简化研究,假设所取的单位节距呈水平直线运行,且每个节距内参与接触的滚珠数相同(为n个)。螺旋滚动导轨单个节距的整体受力情况简化的力学模型,如图2所示。为滚珠的半径,为导轨沟槽和驱动链条沟槽的圆弧半径。
根据自堆式螺旋速冻机的工作原理[3-4],导轨系统所受载荷位于驱动链条右侧边缘,作用点为A点,滚珠同沟槽的接触压力为F1,接触角为β。导轨系统左侧与塑料挡块接触处分别受支持力FN和F2,式中:F2作用点为B点。在垂直方向受力满足:


图2 螺旋滚动导轨单个节距的力学模型Fig.2 The Mechanical Model of Single Pitch of Spiral Rolling Guide
根据Hertz接触理论,单个滚珠的法向接触力同变形之间满足[5]:

式中:δ1—单个滚珠在接触力F1的作用下产生的弹性变形;kh—Hertz接触常量,它由滚动导轨系统中相接触部分的几何尺寸及其材料特性所决定,即:

式中:μ—与弹性变形区椭圆偏心率有关的系数;Ci—Hertz接触理论的材料特性;v1、v2—滚珠和沟槽(驱动链条、导轨)材料的泊松比;E1/GPa、E2/GPa—滚珠和沟槽(驱动链条、导轨)材料的弹性模量;Σρ/mm-1—滚珠与沟槽接触的综合曲率。
通常,在导轨系统的装配过程中,为消除滚珠与沟槽间的间隙并提高导轨系统的接触刚度,会对导轨系统施加预紧力[6]。假设在预紧力的作用下,每个滚珠所受法向接触力均为F0,其弹性变形为δ01,它们之间满足:

同时,在预紧力的作用下点B处受压力F′2,弹性变形为 δ02,B点处压力满足:

在外载荷的作用下滚珠发生弹性变形,假设导轨沟槽和驱动链条沟槽与滚珠始终紧密接触,则驱动链条以导轨和滚珠的接触点C为旋转中心有小角度的旋转。导轨系统的相对变形ΔZ可用点A的相对垂直位移表示,即:

由于驱动链条相对塑料挡块弹性模量大,假设驱动链条在受力过程中不发生变形,则点A的相对垂直位移与点B的相对垂直位移满足:

式中:a—A点与C点的水平距离;b—C点与B点的水平距离。
将式(8)、式(11)代入式(14)得:
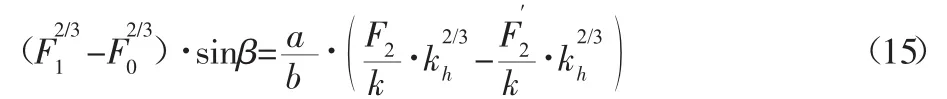
式中:k—塑料挡块的弹性系数。
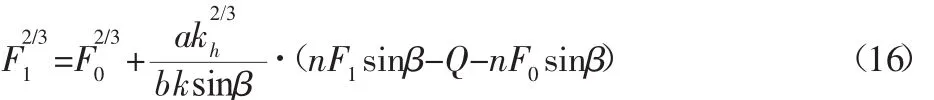
式(16)建立了螺旋导轨系统中滚珠所受压力F1同外载荷Q和预紧力F0之间的函数关系,表达为:

将式(17)代入式(8)和式(13)可得:

式(17)建立了导轨系统外载荷同相对变形ΔZ之间的函数关系。进一步将式(16)对Q求导,将式(18)对ΔZ求导,联立可获得导轨系统法向接触刚度的表达式:

由式(19)可知螺旋滚动导轨系统驱动链条法向接触刚度受预紧力以及外载荷的影响,且为非线性的。
4 实例计算与仿真分析
4.1 螺旋滚动导轨的相关参数
以国产某型号自堆式螺旋速冻机为分析对象,其主要参数,如表1所示。

表1 螺旋滚动导轨的的主要参数Tab.1 The Main Parameters of Spiral Rolling Guide
螺旋滚动导轨系统中的导轨、滚珠以及驱动链条均采用钢制材料,弹性模量为206GPa,泊松比为0.3,塑料挡块采用尼龙1010材料,弹性模量E为1.07GPa,与驱动链条单位节距内有效接触面积S为114mm2,有效接触长度l为1.5mm,由此可得塑料挡块在受力时的弹性系数k为:
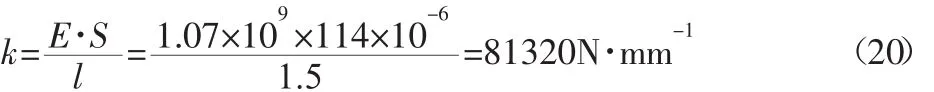
在Hertz接触理论中当曲率比f≥0.6时,最大接触应力与接触尺寸误差比较小,当曲率比f≥0.54时,接触尺寸误差与最大应力误差分别为2.40%和4.63%,当f≤0.54时误差会越来越大,甚至不能使用[7-8],而该螺旋滚动导轨的曲率比在误差允许范围内,因此适用于Hertz接触理论求解。
根据以上参数,滚珠与沟槽接触的综合曲率为[9]:
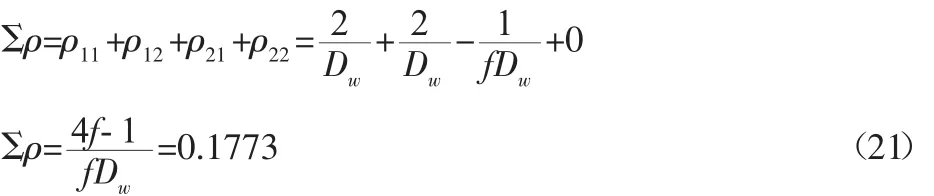
主曲率函数为:
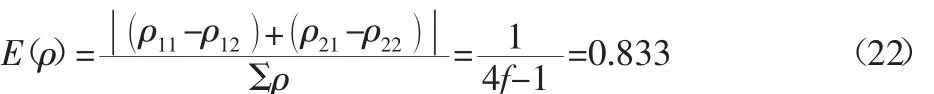
根据主曲率函数 F(ρ)值,查表[10]可得 μ=0.765。
将以上各参数代入式(8)、式(9)、式(10)中,可得:
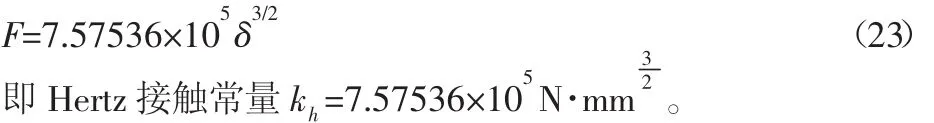
4.2 螺旋滚动导轨系统接触刚度的求解
式(23)建立起了单个滚珠-沟槽接触变形和接触压力间的函数关系,将式(23)对变形量求导可得法向刚度:

从式(23)、式(24)中可以看出滚珠-沟槽间的接触变形是非线性的,接触刚度随着变形量的增加而逐渐增大,但增长幅度在逐渐减小。由此可以看出,适当地对导轨系统施加预紧力可以有效提高导轨系统的接触刚度。
所分析的自堆式螺旋速冻机正常工作时,驱动链条所受外载荷一般小于6083kg,根据内外螺旋导轨的尺寸,假设每个节距的驱动链条受力均匀,则外导轨和内导轨单位节距所受外载荷分别约为195N和310N。故取外载荷,求解不同预紧力下螺旋滚动导轨系统的法向接触刚度。预紧力取4个等级,分别为500N、1000N、1500N、2500N。根据式(16)和式(18)可绘制出外载荷同相对变形之间的关系,如图3所示。根据式(19)可进一步绘制外载荷同导轨系统法向接触刚度之间的关系,如图4所示。

图3 不同预紧力下外载荷同导轨相对变形之间的曲线关系Fig.3 The Curves of Relationship Between the External Load of Different Pre-Tightening Force and Relative Deformation of Guide
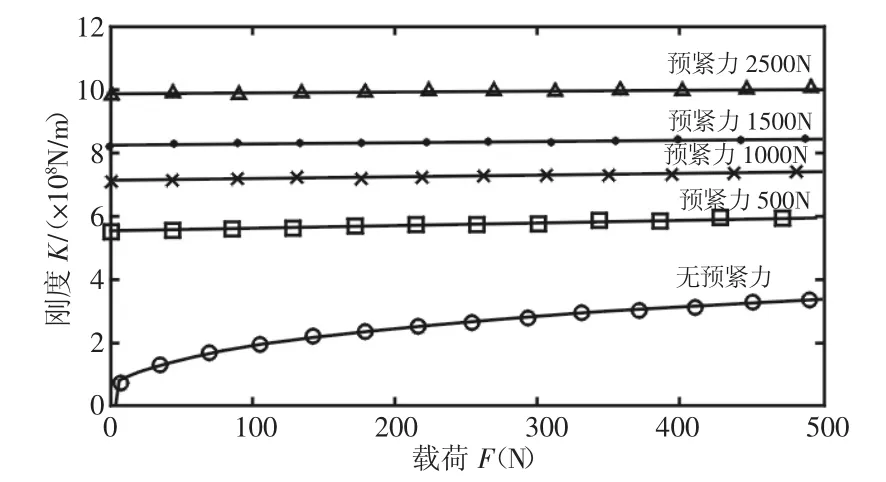
图4 不同预紧力下外载荷同导轨接触刚度之间的关系曲线Fig.4 The Curves of Relationship Between the External Load of Different Pre-Tightening Force and Contact Stiffness of Guide
从图3、图4中可以看出在无预紧力条件下螺旋滚动导轨的相对变形较大,导轨接触刚度小而且受载荷影响较大,而导轨系统在有预紧力的条件下相对变形小,接触刚度大,受外载荷影响小,此时可以近似导轨的接触刚度为常数。在4个不同预紧力等级下,导轨的接触刚度随着预紧力的增大而显著增大,但较大的预紧力也会使得驱动链条与塑料挡块接触处的压力P2增大,从而增大该处的摩擦力,使得塑料挡块加剧磨损。联立式(7)和式(15)可绘制出不同预紧力下外载荷Q同P2之间的关系,如图5所示。在无预紧力的条件下P2受外载荷的影响较大,在有预紧力的条件下P2几乎不受外载荷的影响,但随着预紧力的增加P2明显增大。

图5 不同预紧力下外载荷同塑料挡块所受压力之间的曲线关系Fig.5 The Curves of Relationship Between the External Load of Different Pre-Tightening Force and Pressure on the Plastic Block
因此,在螺旋滚动导轨的应用中,在系统相对变形允许的范围内适当增加预紧力,并使塑料挡块所受压力适中,从而在不大幅加剧塑料挡块磨损的情况下减小导轨的变形,提高导轨的稳定性。
4.3 螺旋滚动导轨系统的有限元分析
为了验证所建立的模型的合理性,下面对螺旋滚动导轨系统在ANSYSWorkbench中进行有限元分析。为了简化导轨系统三维模型的建立以及提高ANSYSWorkbench的求解速度,所建立的导轨系统模型只包含一个滚珠,如图6所示。
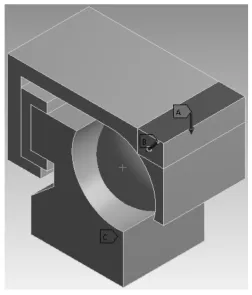
图6 导轨系统实体模型Fig.6 The Entity Model of Guide System
图中:A处—外载荷的作用;B处—预紧力的施加;C处—导轨的约束,其中,外载荷为Q/n。在对螺旋导轨系统模型前处理完毕后,在ANSYSWorkbench中对滚珠-沟槽接触变形进行求解,求解结果,如表2所示。
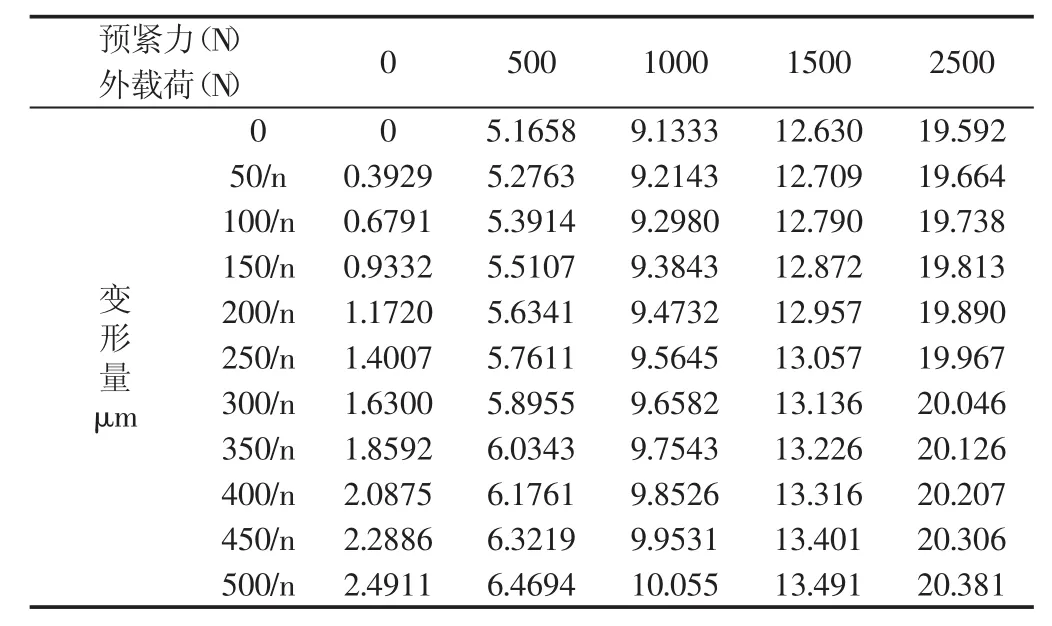
表2 ANSYS Workbench求解结果Tab.2 The Calculation Results in ANSYS Workbench
当外载荷为0时,滚珠的变形由对应的预紧力产生,大小为δ01。将表2中的数值代入式(13)中可绘制出外载荷同相对变形ΔZ之间的关系,如图7所示。
通过对比不同预紧力下导轨系统相对变形的理论模型解与仿真解,如图3、图7所示。可以看出模型理论求解结果与有限元仿真结果具有较好的一致性,从而说明了上述螺旋导轨系统建模方法的合理性以及理论模型的正确性。因此,对实际中螺旋导轨的装配和预紧具有一定的指导意义。
5 结论
(1)根据自堆式螺旋滚动导轨的工作原理对其空间位置和布局进行了分析,并提出了导轨结构合理性、紧凑性及螺旋塔成形稳定性需要满足的条件。(2)根据导轨系统中单个滚珠-沟槽的Hertz接触模型和对自堆式螺旋速冻机螺旋滚动导轨的局部受力分析,完成了导轨系统相对变形的建模和接触刚度的建模。(3)以国产某自堆式螺旋速冻机导轨为分析对象,求解了4种不同预紧力等级下外载荷同相对变形和接触刚度K之间的关系,结果表明在一定范围内预紧力越大,导轨相对变形越小,刚度越大;同时,塑料挡块所受压力随预紧力的增大而显著增大。(4)对导轨局部建立三维模型后进行有限元仿真,求解结果与理论模型的求解结果具有较好的一致性,证明了理论建模方法的合理性与模型的正确性。

