风力机叶片裂纹尖端温度场数值模拟

王琳琳 ，陈长征 ，周 勃 ，张亚楠

1 引言

随着环境和能源问题的日益严峻，可再生能源的发展，尤其是风力发电已越来越重视。叶片是风力机能量转换的主要部件，有叶片和轮毂组成的风轮是能量捕获机构，并将风能转变为机械能，叶片有是风力机力源，主要承载部件，对整个风力机安全运行起着关键作用[1]。风力机叶片是玻璃纤维环氧树脂复合材料，它具有重量轻、强度高、加工成型方便、弹性优良、耐化学腐蚀和耐候性好等特点，已被广泛应用到很多领域。但其生产中会经常出现各种各样的微缺陷（如微裂隙、微空洞等），而这些微缺陷会随着叶片复合材料的周围环境、受载情况变化产生裂纹萌生、扩展最后使材料断裂损伤。裂纹萌生后，微裂纹处不可逆的局部塑性变形导致裂纹萌生区温度急剧升高，大部分塑性功转化为热能，会以热的形式释放出来，从而使裂尖出现热传导形成温度场。因此，风力机叶片疲劳裂纹扩展是一个热耗散的过程，而裂纹内部温度场的变化反映材料的疲劳损伤过程。

大多数学者对材料的Ⅰ型、Ⅱ型裂纹有深入研究，但是实际工程问题中，受力构件不一定是对称的，载荷也不一定是对称的或反对称，构件中裂纹尖端的应力场，Ⅰ型、Ⅱ型和Ⅲ型的应力场可能同时存在，裂纹的形式也是各种各样的，因此裂纹经常处于三种基本类型或任意二种基本类型的复合变形条件下[2]。复合型裂纹与单纯张开型裂纹扩展主要在于裂纹不按原裂纹原方向扩展，而且失稳条件很复杂等特点，所以分析研究复合型裂纹的温度场是至今较难的课题。

国内外许多学者研究了各种材料的裂纹尖端温度场疲劳损伤识别的方法。文献[3]计算了裂尖塑性区的热源变化过程，实验中总结热源强度大小对裂纹扩展有着重要的影响。文献[4-5]采用红外热像无损检测验证了疲劳过程的热平衡方程，研究热源耗散的耗散规律。文献[6]对疲劳过程中耗散能进行了研究并拟合耗散能—疲劳寿命曲线，并用红外成像仪监测材料的温度信号。文献[7]对纤维增强复合材料层合板采用能量耗散方法研究，结果得出复合材料层合板内部损伤与能量耗散有关系的。前人研究说明采用能量方法能够分析材料的温度场变化，有助于明晰材料疲劳损伤机理。因此，采用能量理论的热耗散方法研究风力机叶片复合材料的疲劳损伤机理。

裂尖温度场分布除了取决于材料的热物性参数外、还与裂尖塑性过程区裂纹开裂角因素有关[8]。因此以裂尖塑性过程区的开裂角为参考依据，分析风力机叶片复合裂纹尖端的温度场分布规律，以明晰风力机叶片裂纹扩展机理。

2 裂纹尖端应力场分析

根据复合材料力学的Tsai-Hill屈服准则为[9]：

式中：F、G、H、L、M、N—复合材料正交坐标系下的强度系数，所有值通过单轴拉压和纯剪切试验确定；σx、σy、σz、τyz、τzx、τxy—复合材料正交坐标系下应力分量。

单向复合材料可视为横观各向同性材料，则X为沿纤维方向的强度，Y为垂直纤维方向的强度，S为在剪切强度，因此有：

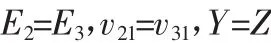
平面应力状态下，有σz=τzx=τvz=0，正交各向异性材料的Tsai-Hill强度准则表达式为

图1 复合裂纹尖端应力场Fig.1 Stress Field of Composite Crack Tip

图中：β—裂纹倾角；2a—裂纹长度；σ0—远处作用的应力。复合型裂纹尖端应力场为：

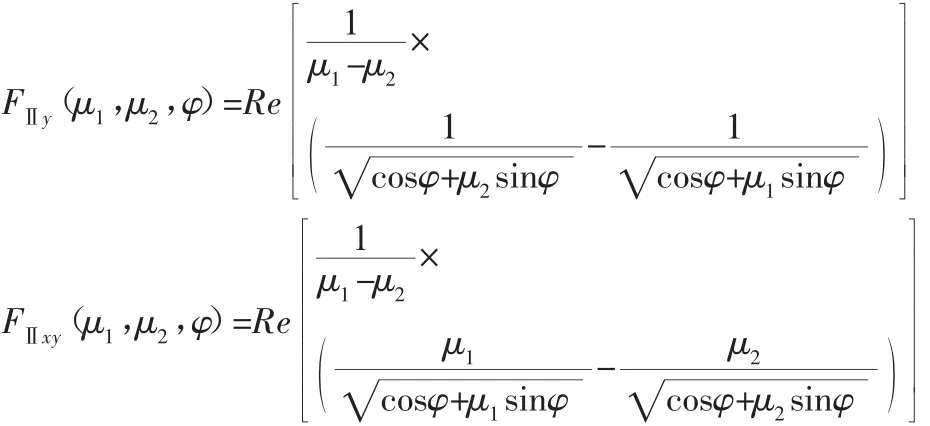
式中：η=KⅡ/KⅠ；K=σ0；KⅠ=K sin2β；KⅡ=K sinβcosβ；KⅠ—Ⅰ

型裂纹应力强度因子；KⅡ—Ⅱ型裂纹应力强度因子，设μ1

和μ2为特征方程式（3）的根：

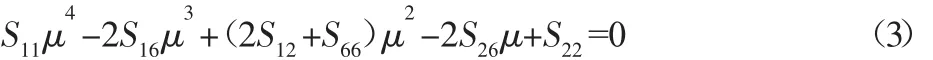
式中：Sij—各向异性材料的柔性系数。

对于正交各向异性材料，弹性主轴（X，Y，Z）与坐标轴（1，2，3）重合，得到本构方程关系式为：

则塑性区半径为：

此区域就是温度场。

3 各向异性材料温度场

裂纹扩展时发生塑性变形，在塑性区内取一个微元体，它的塑性功增量为 d WP=dεp；—等效应力；dεp—等效塑性应变。则整个变形体在塑性变形时所消耗的塑性功为：

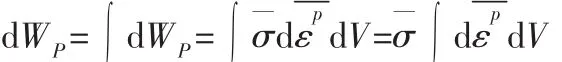
式中：η—热耗散因子是热耗散速率与塑性功速率的比值。如果η确定后，则可以通过塑性功速率d WP计算出任意位置的热源强度：Q=βWP=η

（80～100）%塑性能在裂纹扩展的过程中以热能的耗散形式释放，选用90%塑性能作为热能的量[1]。热弹性效应和其它热损失量远远小于塑性热耗散量，外部热源不考虑，则耦合的热传导方程为：

复合材料是各向异性材质，则其热传导也是各向异性的，导热系数是一个二阶张量，包含 9 个分量 λij，i，j=1，2，3。热流密度在正交坐标系中沿3个坐标轴方向的温度梯度的线性组合为：

把式（6）代入式（5）整理得：

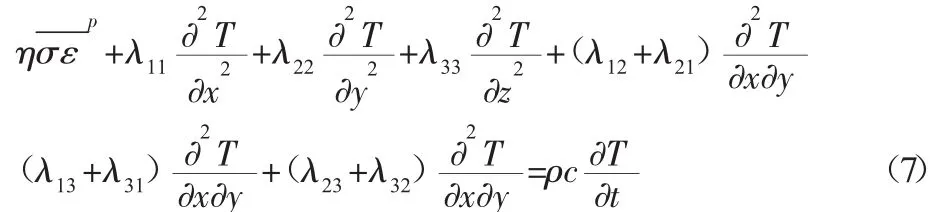
根据昂赛格互易关系：λij＝λji，i，j=1，2，3

正交各向异性复合材料有三个相互垂直的弹性主轴，即x、y、z为主轴方向，相应的主导热系数为 λr、λt、λa，3 个主轴建立正交坐标系，可把式（7）简化为：

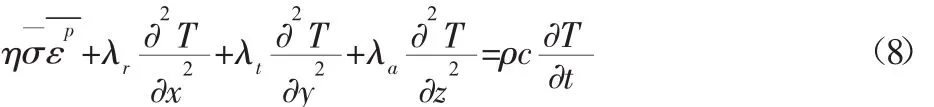
作空间变量变换，令：

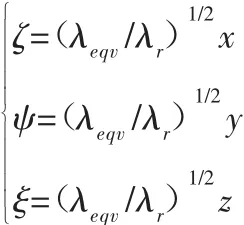
式中：λeqv称为等效导热系数，上式代入式（8）：

等效导热系数与 3 个主导热系数间的关系：λeqv＝（λrλtλa）1/3

4 模拟计算

4.1 有限元建模

取长为30cm，宽为15cm，高为50cm，边界带有预制15mm长的微小裂纹玻璃纤维増强复合材料为研究对象，微小裂纹角度分别取0°开裂角和45°开裂角。玻璃纤维增强的材料属性如下：密度ρ=2550kg/m3；导热率λ=1.0W/（m·k）；比热容c=1920J/（kg·K）；空气的物理参数密度ρ=1.2kg/m3；导热率λ=0.0259 W/（m·k）；比热容c=1005J/（kg·K）玻璃纤维复合材料为各向异性材料。

对模型选用断裂分析中裂纹的20节点等参单元SOLID186单元，该单元是在裂尖是奇异单元模型。预制裂纹附近的网格划分比较密集，有助于计算的精度高。

初始温度室温20℃，试验在密闭的室内进行。在模拟过程中，忽略边界的热传导，热辐射的作用，因为它们对复合材料裂纹扩展时产生的温度场影响很小可以忽略不计。

采用ANSYS软件分析模拟玻璃纤维复合材料的温度场[10]，模拟过程中首先将正交各向异性复合材料上下施加固定载荷，对其进行力学分析，然后根据能量释放率准则判断裂纹是否扩展，如果裂纹扩展，再进行热力耦合计算分析其温度场；如果裂纹并没有扩展，继续加载载荷，直到裂纹扩展模拟裂尖的温度场。

4.2 计算结果

图2 0°开裂角裂纹温度场分布图Fig.2 Field Distribution of 0°Crack Temperature

图3 45°开裂角裂纹温度场分布图Fig.3 Field Distribution of 45°Crack Temperature

图2 和图3为0°开裂角和45°开裂角裂纹模型分别在5s、15s、25s、35s的温度场分布图，图4为0°和45°开裂角裂纹与解析解的温度曲线对比图。从图2和图3中，可以看出0°和45°开裂角裂纹模型的温度变化趋势大致是一致的，先是温度有小幅的增高，随着时间的增加温度缓慢的增高，等到25s后温度变化趋势大温度升高比较快。图2和图3中0°和45°开裂角裂纹在每个时间塑性区形状是相同的，只是时间长塑性区范围比时间小塑性区范围大，因为有载荷施加裂纹会扩展，所以塑性区范围随时间变化越来越大。图4中可以看出45°开裂角裂纹的温度比0°开裂角裂纹的温度在同一时刻时温度略高一些，原因是带角度的裂纹塑性变形区比没有角度的裂纹塑性变形区大；还会发现解析解与0°开裂角裂纹温度的对比，误差不超过5﹪符合实际要求。说明采用此方法可以分析各向异性复合材料的不同角度的预制裂纹的温度场分布，有利用工程中对材料含裂纹损伤提供有利的理论参考，预防裂纹的萌生、扩展和断裂。

5 结论

0°开裂角裂纹数值与解析计算结果对比误差在5%内；0°和45°开裂角裂纹的温度变化先是小幅度升高，再随时间温度迅速的升高；0°和45°开裂角裂纹的温度对比，有角度的裂纹对各向异性复合材料的温度场影响大，因此预防有角度开裂角裂纹是很有必要的。综上所述，应用能量理论中的热耗散是很有效的考察裂尖的温度场方式，有助于对叶片复合材料疲劳损伤的研究。

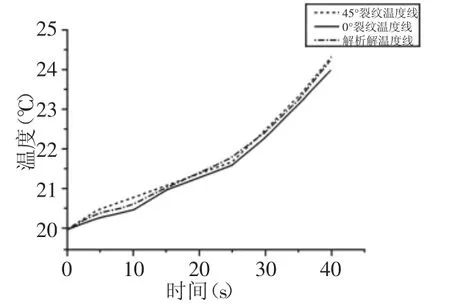
图4 温度曲线图Fig.4 Chat of Temperature Curve