电流与振动信号融合的转子系统故障诊断研究
石江波 ,杨兆建 ,郭伟杰 ,李 峰
1 引言
转子系统是旋转机械的核心部件,在工程实际中应用广泛,而转子系统是否能够正常运行与生产、安全息息相关,传统的故障诊断方法都是以分析振动信号作为诊断的手段,信号过于单一。运用振动信号及电机电流信号相融合的分析方法可充分利用两种信息改善传统方法故障识别率不高,并能识别区分传统方法不易区分的几种转子系统故障[1-2]。
文献[3]结合小波包能量谱分析和共振解调法,将其用于声发射信号的特征能量提取中。文献[4]在轴承的故障诊断中运用小波包分解提取信号的能量谱,再用包络分析得到功率谱。文献[5]在航空发动机转子实验器上模拟了碰摩故障,运用小波包分解提取特征向量,运用支持向量机法进行训练测试并进行故障识别。文献[6]运用谐波小波包技术提取特征向量,提高了转子故障识别准确率。文献[7]采集转子同一截面不同方向的振动信号结合小波包络解调及全矢谱数据融合技术对旋转机械调制信号进行分析,得出的结果优于基于全矢谱的传统包络解调分析。文献[8]提取电机电流信号,运用小波包方法提取信号特征能量谱,再运用BP神经网络实现对转子系统扭矩激励的识别。文献[9]为解决轴承故障诊断中特征量提取困难问题,提出了基于小波包与奇异值分解的GA-SVM滚动轴承故障诊断方法。文献[10]建立汽车发动机故障诊断贝叶斯网络,利用贝叶斯网络进行信息融合完成其故障诊断目标。文献[11]提出基于多源信息融合的贝叶斯网络故障诊断方法,并对滚动轴承进行了故障诊断。文献[12]运用贝叶斯网络于转子系统故障诊断,提出一种用于转子故障诊断的网络框架,且考虑了实际运行工况及故障征兆,并得到了良好的诊断效果。文献[13]提出一种基于振动频谱分析和贝叶斯网络的转子振动故障诊断方法,运用作者改进的优化分簇算法构建振动故障的贝叶斯网络,用贝叶斯网络进行故障概率计算进而识别故障类型。综上所述,大部分的文献都是通过振动分析方法来研究转子系统的故障,运用的信号较单一,而提取运用电机电流信号分析转子系统故障的研究相对较少。
因此,针对转子系统的几种典型故障,在单跨转子试验台上模拟转子系统的不平衡、不对中、碰磨故障,并采集不同故障类型下拖动电机的电流信号及不同位置的振动信号,利用小波包能量法对采集的信号进行特征值提取,然后对特征值进行归一化,最后利用贝叶斯网络对转子系统故障进行识别。
2 试验台及试验操作
2.1 转子试验台
转子试验台示意图,如图1所示。转子实验台实物图,如图2所示。保持电机转速为500r/min,分别在无故障、转子不平衡、不对中、转子碰摩四种故障类型下采集两个不同位置的x和y向的振动信号以及电机电流信号,振动信号由四个压电式加速度传感器采集,电机电流信号通过直流电流变送器最终都接入数据采集仪实现数据采集。所研究的故障类型与故障编号对照表,如表1所示。

图1 转子系统实验台示意图Fig.1 Sketch of Test Bed of Rotor System

图2 转子试验台Fig.2 Bed of Rotor System

表1 故障编号与故障类型对照表Tab.1 Comparison Between Fault and Fault Types
3 小波包分解特征提取
3.1 小波包分解原理

图3 三层小波包分解结构图Fig.3 Structure of Wavelet Packet Three Layer Decomposition
小波法可很好的细化分析信号低频段特征信息,小波包法可以对整个频率段进行细化分析提取特征量,克服了小波法对高频段分析欠缺的不足。小波包分解可多层次划分频段,并可根据实际需要对整个频带进行任意层次的细分,可提取出需要的各个细化频带的能量特征值。每个频带都是正交的,且无交叠无遗漏相互独立。小波包三层分解过程示意图,如图3所示。

式中:h(k)、g(k)—双尺度系数,且 g(k)=(-1)kh(1-k)即两系数具有正交关系;u0(t)—正交尺度函数;u1(t)—小波基函数。式(1)即为构造的序列为由基函数u0(t)确定的正交小波包。
由于研究的转子系统故障为转子不平衡、转子不对中及转子碰摩,这几种故障均对各频带内能量值有较大影响,故以能量值作为特征向量的元素是完全合理的。对实测的各故障状态振动及电流信号进行小波包变换,得到a层分解各层特征向量,其中M为信号自频带数量。总信号为S=S0a+S1a+S2a+…+SMa。得各自频带能量:

式中:xmk(m=0,1,…,M;k=0,1,…,n)—信号 SMa的离散点的幅值。最后对能量向量E进行归一化处理,得到能量特征向量,即小波包能量谱。第一组部分振动信号各频段特征能量值,如表2所示。

表2 第1组振动信号各频段特征能量值(部分)Tab.2 First Groups of Vibration Signal Characteristic Energy Value of Each Frequency Band(Part)
4 贝叶斯分类方法
4.1 基于贝叶斯的故障诊断过程
(1)根据多传感器信息融合的广义定义,利用贝叶斯参数估计算法对小波包法提取并经过归一化处理的故障特征信息进行多特征信息融合,得到最大后验估计值的计算公式。
(2)运用训练样本根据贝叶斯网络的构建过程,通过NBN(朴素贝叶斯)分类器确定故障特征信息与故障模式之间的关系。
(3)利用建立的NBN分类器简化最大后验估计值公式,得到转子系统的贝叶斯网络故障诊断模型。
(4)通过测试样本验证故障诊断模型的有效性并完成诊断。

图4 故障诊断过程Fig.4 Fault Diagnosis Process
转子系统的故障诊断过程,如图4所示。先采集若干组样本数据,再用三层小波包分解提取初步能量谱,然后对初步能量谱进行归一化处理,将特征值输入贝叶斯网络进行学习,最后将待识别故障信号的特征向量输入贝叶斯网络进行故障识别。
4.2贝叶斯分类器设计
从该故障诊断的方法出发,设计了两个分类器。在对两种故障模式的分类识别诊断中,给出了判别函数的概念并利用NBN分类器简化了判别函数。在多故障模式的故障诊断中,选择用NBN分类器来简化信息融合最大后验概率估计值公式并建立故障诊断模型。
设 Y={Y1,Y2,Y3,…,Yn},X={X1,X2,X3,…,Xn}。其中Y表示故障模式类别,X表示特征向量空间。对提取的特征向量进行融合,融合后的最大后验概率估计值为:
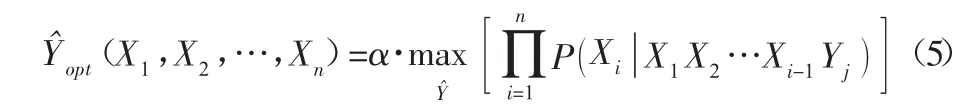
由此采用NBN分类器,假设特征向量之间相互独立,每个属性节点Xi与故障类节点Yi相关联,这种假设降低了贝叶斯网络构建的复杂性。因此通过构造分类器可将式(5)表示为:

式(6)是信息融合与贝叶斯网络相结合的推理结果。通过式(6)计算出最大后验概率估计值,相对应的Yj类为诊断后得出的故障类型。
4.3 贝叶斯网络建立与诊断
贝叶斯网络包括两个基本事件层:故障征兆层、故障层,这两个事件之间具有直接的因果关系。转子系统实际故障类型较多,但是其常见故障基本都是转子不平衡、不对中、转子碰摩这几种。需要识别转子系统是否有故障,因此无故障作为一种事件类型加入故障事件层。故障事件层节点选取转子系统几种典型故障,即无故障、转子不平衡、不对中、转子碰摩。
故障征兆层:对4组振动信号,1组电流信号分别进行三层小波包分解提取能量谱,再进行归一化处理得到最终能量谱。
根据以上贝叶斯网络故障诊断的一般框架,可以建立转子系统常见故障的贝叶斯诊断网络。贝叶斯诊断网络共两层,44个节点,如图5所示。

图5 转子系统故障诊断贝叶斯网络模型Fig.5 Bayesian Network Model of Rotor System Fault Diagnosis
4.4 诊断准确率对比
为了检验运用融合信号进行转子系统故障诊断与只用振动信号或电机电流信号进行故障诊断的正确率,分别设定15,30,45,60,75,90,105,120 组样本输入贝叶斯网络进行学习,其诊断准确率对比曲线,如图6所示。
从图6可以看出三种信号模式下诊断准确率都随着样本数的增多而增大,只采用电流信号进行诊断准确率最低,采用振动信号准确率次之,采用融合信号准确率最高而且比较稳定。无论样本数量是多是少,运用融合信息的诊断准确率均大于采用单一信号的正确率。

图6 三种信号模式诊断准确率比较图Fig.6 Diagnosis Accuracy Comparison Chart of Three Signal Patterns
5 结论
搭建单跨转子试验台,采集几种典型故障类型下的电机电流信号及两个不同位置的和向的振动信号,利用小波包能量法提取故障特征向量,并将其提取的特征向量进行归一化处理,然后将样本数据的特征向量输入贝叶斯网络进行学习,最后将待识别数据的特征向量输入贝叶斯网络进行故障识别。结果表明:采用融合信号的贝叶斯网络诊断准确率高于运用单一信号进行故障诊断的正确率。即使在小样本下采用融合信息进行故障诊断准确率也比较高,可以满足诊断精确度的要求。

