四轮驱动电动汽车车速估计与DYC控制研究

李 军，张胜根，隗寒冰

1 引言

四轮独立驱动电动汽车因其四个车轮独立可控的特点，在其行驶的不同工况中，车辆动力学相较于传统车辆也更为复杂。在对四轮驱动电动汽车进行横向稳定性控制时，需要分配内侧车轮与外侧车轮的力矩从而控制车辆的横摆力矩，此种车辆横向稳定性控制方法即为直接横摆力矩控制（Direct Yaw-moment Control，DYC）[1]。

在以横摆力矩控制为代表的车辆稳定性控制以及车辆主动安全控制中通常需要对车轮滑移率进行监测而判断轮胎的运动状态从而对车轮转矩加以控制。而滑移率的监测与控制有赖于精确的车速信息[2]。四轮驱动汽车因没有非驱动轮，其车速不能依据传统二轮驱动车辆那样由非驱动轮轮速计算而得[3]。

能否获取精确的汽车动力学控制的状态信息和道路信息，已经成为汽车底盘控制系统发展急需解决的关键问题。

2 基于EKF的车速估计

卡尔曼滤波算法能对运行状态进行实时估计和预测，广泛应用于控制、制导等现代工程中[4]。对于车辆行驶状态参数的估计这一非线性系统工程问题，扩展卡尔曼滤波算法（Extended Kalman Filter，EKF）能够很好的适应计算的需要从而得以应用[5]。建立非线性三自由度汽车模型，如图1所示。

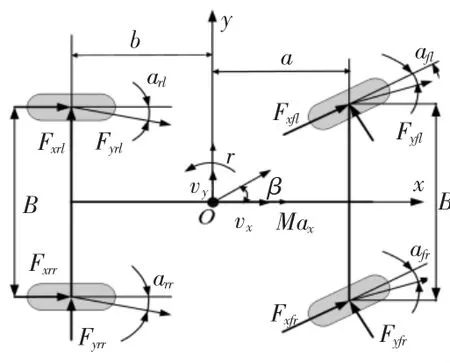
图1 非线性三自由度汽车模型Fig.1 Nonlinear Three Degree of Freedom Vehicle Model

由以下非线性三自由度车辆运动微分方程式（1）、式（2）可以求得在一定的纵向速度下稳态横摆角速度和侧偏角。

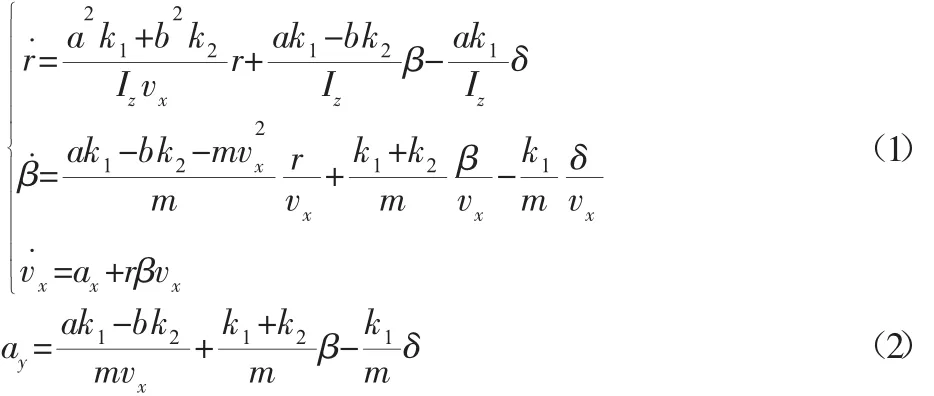
式中：r—横摆角速度（rad/s）；β—质心侧偏角（rad）；v—纵向车速（m/s）；δ—前轮转角（rad）；ax—纵向加速度（m/s2）；ay—侧向加速度（m/s2）；m—整车质量（kg）；Iz—整车绕 z轴的转动惯量（kg·m）；a—质心距前轴的距离（m）；b—质心距后轴的距离（m）；k1—前轴等效侧偏刚度（N/rad）；k2—后轴等效侧偏刚度（N/rad）。

车速估计算法中的状态变量为 x（t）=（r，β，vx）Tt；输出变量为y（t）=（ay）；控制变量变量为 u（t）=（δ，ax）Tt；车速估计算法在Matlab/Simulink环境下实现。为了验证估计算法的有效性与准确性，以四轮驱动电动汽车为研究对象，仿真采用CarSim中成熟的四轮驱动电动车辆为模型，模拟实际车辆直道与静态转向试验工况。借助Simulink仿真平台建立扩展卡尔曼滤波车速估计算法，以纵向加速度、转向盘转角作为输入，融合EKF算法估算纵向车速，并将EKF估计值与仿真值进行了对比分析。分别在路面附着系数0.85、0.5、0.2的均一路面和0.2L/0.5R的分离路面上进行仿真。在不同路面附着系数的均一对开路面及分离路面上分别进行直行试验与静态转向试验，得到驱动工况与制动工况下EKF估算值与仿真值的绝对误差，如表1所示。

表1 车速估计绝对误差表Tab.1 Absolute Error of Vehicle Speed Estimation

由表1可知在路面附着系数相同的均一对开路面，驱动车速误差小于制动车速误差，说明制动时，车轮发生了抱死；同一路面附着系数的均一对开路面上，无论是驱动还是转向，车辆直行车速误差小于静态转向误差，表明在转向时，车辆横摆角速度较大，车辆两侧轮速不同，部分车轮发生滑转现象；对于对开路面，转向时的车速误差显著大于直行时的车速误差，进一步分析，这是因为单侧车轮滑转获抱死导致整车出现横摆现象，对于此种情况，为得到较为准确的车速估计值，需通过运动学模型计算车速对加速度积分的计算值进行修正。

3 直接横摆力矩控制策略

直接横摆力矩控制是通过对比名义横摆角速度与传感器得到的实测横摆角速度，判断当前车辆状态是不足转向还是过多转向[6]。根据名义横摆角速度和传感器得到的实测横摆角速度的偏差计算得到需要施加的主动横摆力矩，选择合适的车轮进行干预。

3.1 横摆角速度与车速的控制

横摆角速度的实际值可以通过横摆角速度传感器直接得到，而车辆质心侧偏角实际值的直接测量比较困难，一般采取估算的方法[7]。控制车速可以通过控制电机输出扭矩来实现，重要的是计算出车辆处于稳定状态的最高车速作为车速上限[8]。如果当前车速Vx大于车速上限Vxup则需要通过CAN总线给电机控制系统发送指令使其降低输出扭矩，从而减小车速。

降扭策略为：

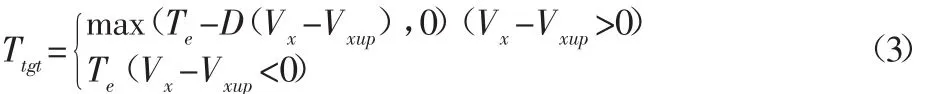
式中：D—表征干预强度的常数；

Ttgt—目标扭矩；

Te—当前的电机输出扭矩。

当前车速低于Vxup，或前轮转角保持较小一定时间并且横摆角速度比较小，则退出扭矩控制。

3.2 不同转向工况下干预车轮的选择

对于分布式驱动汽车，在产生整车横摆力矩时既可以制动某一车轮，也可以驱动某一车轮[9]。下面通过仿真分析了在不同车轮施加驱动力或制动力对整车横摆力矩的影响。

某一试验车在左转的过程中，在某一车轮单独施加驱动、制动力时对整车横摆力矩影响的仿真结果，如图2、图3所示。

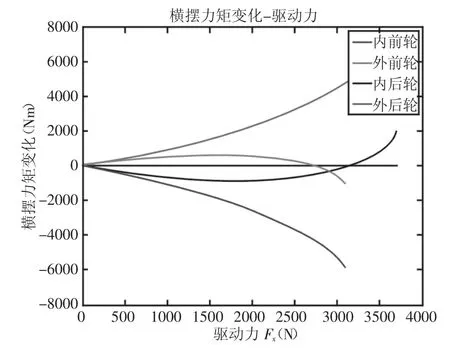
图2 单轮驱动对横摆力矩的影响Fig.2 Effect of Single Wheel Drive on Yaw-Moment

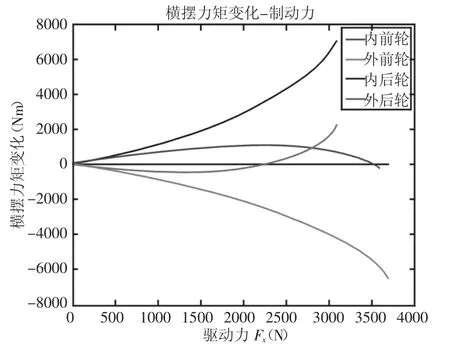
图3 单轮制动对横摆力矩的影响Fig.3 Effect of Single Wheel Braking on Yaw-Moment

从结果可以看出对内后轮制动、外后轮驱动产生的正横摆力矩最大，对外前轮制动、内前轮驱动产生的负横摆力矩最大。因此，可以根据这一结果进行干预车轮的选择。

不同转向工况下驱动轮和制动轮的选择，如表2所示。

表2 不同转向工况下DYC干预车轮的选择Tab.2 Choice of DYC Intervention Wheels Under Different Steering Conditions

3.3 转矩控制策略

分布式电机四轮独立驱动的车辆是执行机构过约束系统，四个电机可以组合起来使用，用于产生期望的牵引力和主动横摆力矩。这就产生了求解控制分配的问题[10]。分布式驱动车辆的控制分配问题，主要目的是在满足四个电机的输出能力约束的情况下，计算出四个电机的各自期望输出力，以产生期望的横摆力矩和牵引力。

四个电机输出能力的等式约束如式（4）所示：

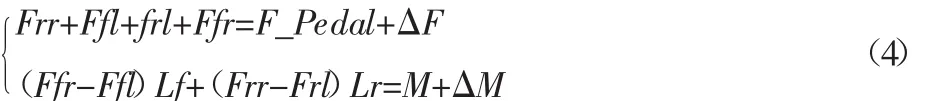
四个电机输出能力的不等式约束如式（5）所示：

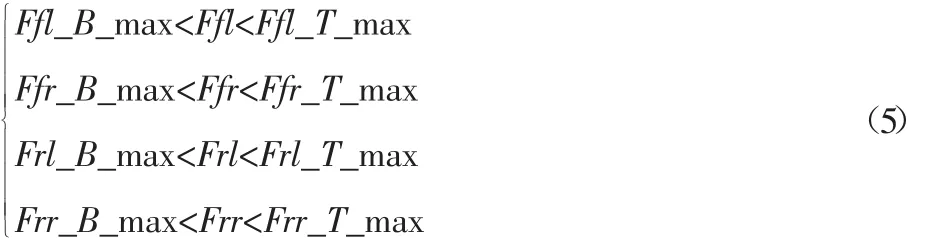
松弛变量为：

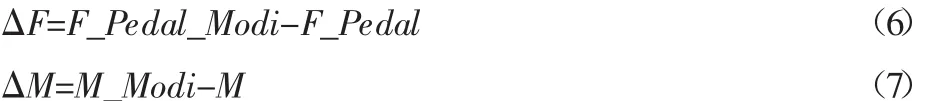
式中：Ffl、Ffr、Frl、Frr—前左电机、前右电机、后左电机、后右电机目标输出力；F_Pedal—期望的牵引力；F_Pedal_Modi—输出的牵引力；M—期望的横摆力矩；M_Modi—输出的横摆力矩；ΔF、ΔM—松弛变量；Ffl_B_max—前左电机最大输出制动力，其他依次类推；Ffl_T_max—前左电机最大输出驱动力，其他依次类推。

电机峰值输出转矩：

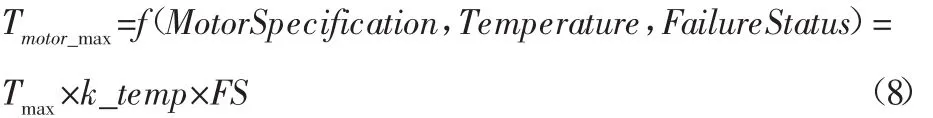
式中：Tmotor_max—电机峰值输出转矩；Tmax—电机设计最大输出转矩；k_temp—电机在系统保护功能（电机过热保护、变频器过热保护）下的输出转矩系数；FS—故障状态开关。

4 仿真分析

在CarSim中建立车辆模型，并与Simulink进行控制系统的联合仿真。在仿真中设定前后轴四轮总驱动转矩为600Nm。

4.1 模型参数与仿真工况

仿真模型的主要参数，如表3所示。

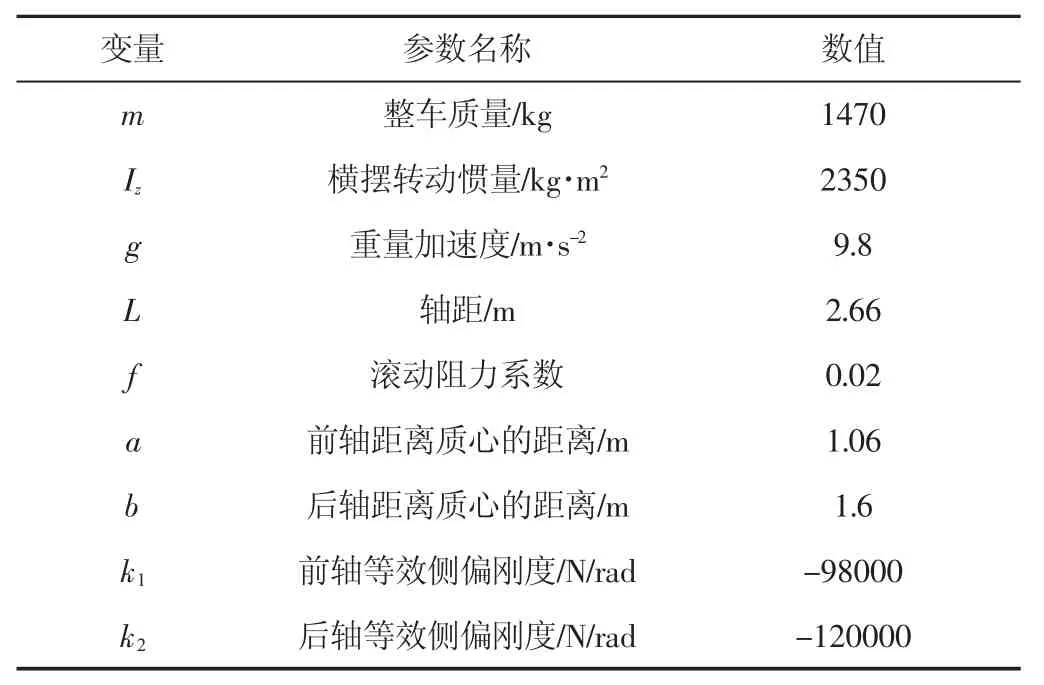
表3 整车主要参数Tab.3 Main Parameters of Vehicle

4.2 仿真结果分析

仿真分别对比了在方向盘角阶跃输入情况下动态转矩分配和后驱两种情形下的车辆状态响应。

方向盘角阶跃输入情况下动态转矩分配和后驱两种情形下车辆纵向车速响应，如图4所示。

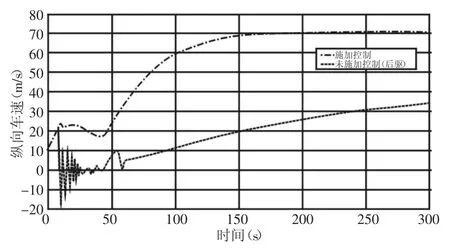
图4纵向车速Fig.4 Longitudinal Speeds

图4 表明，在（5～45）s期间，施加控制的车辆纵向车速有所降低，其原因是此时存在一定程度的车轮滑转，此时控制器重新分配前后轴扭矩，使得在45s之后车轮滑转率回到正常区间，从而纵向车速在45s后能够重新加速。在图4中，无控制的后驱情形则一直存在较为严重的车轮轮胎滑转，导致纵向轮胎力损失较多，所以加速能力不足。

方向盘角阶跃输入情况下动态转矩分配和后驱两种情形下车辆侧向车速响应，如图5所示。

由图5可知，在（5～45）s期间，车辆侧向速度产生振荡，原因是侧偏角过大导致此时轮胎进入了侧向饱和区域。

方向盘角阶跃输入情况下动态转矩分配和后驱两种情形下车辆横摆角速度响应，如图6所示。

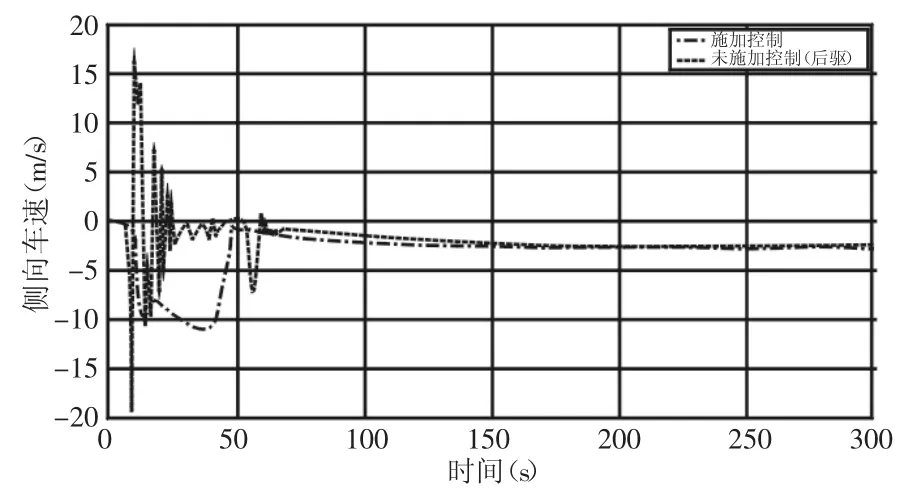
图5 侧向车速Fig.5 Lateral Vehicle Speed

图6 横摆角速度Fig.6 Yaw Rate

在仿真系统中，控制系统横摆角速度偏差的死区环节的死区区域设定为（-1.2～1.2）°。在（0～5）s期间，由于此时方向盘转角为零，故横摆角速度偏差也为0，此时可看作是后驱情形。在第5s后，由于开始角阶跃前轮转角输入，使得横摆角速度偏差为负值，说明此时进入过多转向状态，故PI调节器根据负偏差计算出的值变小，使得驱动力向前轴转移，抑制过多转向。在40s左右，横摆角速度偏差变为正值，说明此时进入不足转向状态，故PI调节器根据负偏差计算出的值变大，使得驱动力向后轴转移，抑制不足转向。所示，在50s以后横摆角速度的偏差已经进入死区区域，PI控制输出不再变化。由图7可知，施加控制的车辆，相对于未施加控制的后驱情形，其横摆角速度处于较稳定的状态。

5 结论

（1）设计了以非线性三自由度整车动力学模型为基础的扩展卡尔曼滤波算法，在不同路面附着系数的均一对开路面及分离路面上进行了仿真实验，结果表明车速估计算法能够准确地估计车辆在直行及转向过程中的车速，绝对误差在0.81m/s以内，能较好地反映车轮滑移率变化，为转矩控制提供了参考。

（2）提出了直接横摆力矩控制策略，分析了不同转向工况下驱动轮与制动轮的干预选择；提出了车轮在非稳定状态下的转矩控制策略，经仿真验证，直接横摆力矩控制策略能够根据横摆角速度的偏差，正确地选择干预车轮，及时地控制车轮转矩，从而保持车辆的横向稳定性。

（3）后续将进一步进行实车试验，以验证直接横摆力矩的实际效果。