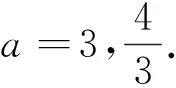全分离、半分离与不分离——例谈含参问题的求解策略

浙江省杭州市富阳区二中 马华明 (邮编：311400)

对于含有参数的方程有解与不等式恒成立问题，我们通常采取的方法是分离变量或不分离而讨论参数，笔者通过最近的学习和尝试，发现采用“半分离”的方法，解有些题目更加方便.今日撰文尽可能将“全分离、半分离与不分离”都呈现出来与大家共享，并请大家批评指正.

例1 若存在实数a，对任意的x∈[0,t](t∈Z)，不等式x|x-a|≤x+4恒成立，则整数t的最大值为______.

法一 (全分离)x=0时，显然成立；

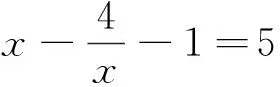
所以整数t的最大值为6.

法二 (半分离)x=0时，显然成立；

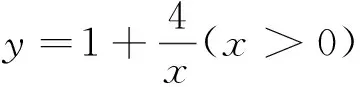
法三 (不分离)要使x∈[0,t](t∈Z)时，x|x-a|≤x+4恒成立，显然，a>0时，t更大.由图知，当直线y=x+4与y=-x(x-a)相切时，t最大且t是方程x(x-a)=x+4的大根，解得

所以t的最大值为6.

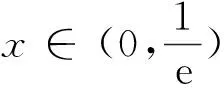
法二 (半分离)

显然a≤0时，g(x)、h(x)无两交点，所以a>0；

当g(x)、h(x)有唯一公共点时，在此公共点有公切线，

设公共点为(x0,y0)，则

法三 (不分离)

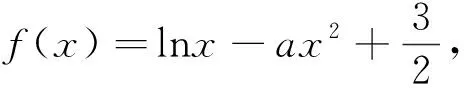
当a≤0时，f′(x)>0，f(x)在定义域上最多一个零点，不合题意，舍去.

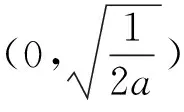
小结 从以上两例可以看出，“半分离”较之“不分离”避免了参数讨论，较之“全分离”又有函数简单的优点，在教学实践中，学生普遍喜欢“半分离”的方法.“半分离”就是把原来含参又复杂的函数分解成一边有参一边无参的两个简单易确定、易作图的函数，再根据题意和图象来寻找答案的方法.

再看下面几道考题，也能发现“半分离”简单易懂.

例3 (浙江省2017年11月学考21题)若不等式|2x-a|+|x+1|≥1的解集为R，则实数a的范围是__________.

法一 (全分离)原不等式可化为，对任意实数x有

a≤2x+|x+1|-1或a≥2x-|x+1|+1，由图知，a≤-4,a≥0.

法二 (半分离)|2x-a|+|x+1|≥1⟹|2x-a|≥1-|x+1|.

例4 (2018年4月浙江学考22题)若不等式2x2-(x-a)|x-a|-2≥0对于任意x∈R 恒成立，则实数a的最小值是______.

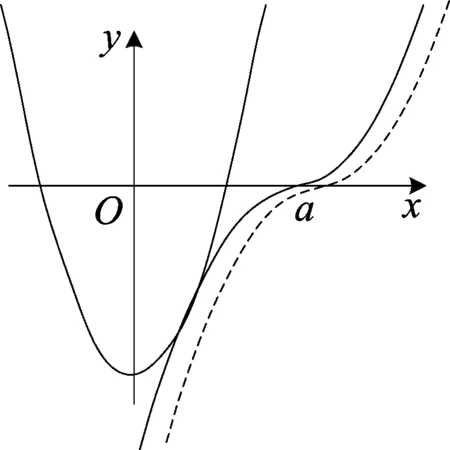
解 (半分离)原不等式化为2x2-2≥(x-a)·|x-a|

例5 (2017年4月学考25)已知函数f(x)=3|x-a|+|ax-1|,其中a∈R.

(1)当a=1时,写出函数f(x)的单调区间;

(2)若f(x)为偶函数,求实数a的值;

(3)若对任意的实数x∈3〗,不等式f(x)≥3x|x-a|恒成立,求实数a的取值范围.

解 (1)(2)略.

(3)由题意知,对任意的实数x∈3〗,不等式|ax-1|≥(3x-3)|x-a|恒成立.

显然,当实数x∈1〗时,不等式|ax-1|≥(3x-3)|x-a|恒成立,

所以只需考虑不等式|ax-1|≥(3x-3)|x-a|对实数x∈恒成立.

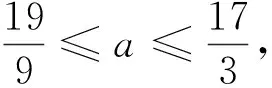
全分离太烦.

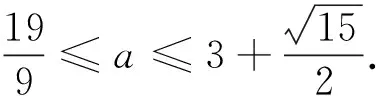
法二 (不分离)ax-1≥(3x-3)|x-a|，分别画出两边的函数图象知，

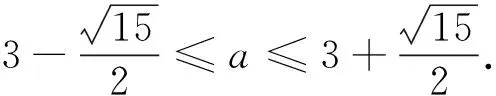
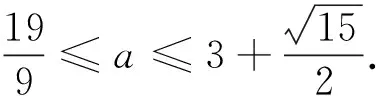
例6 讨论关于x的方程2lnx=x3-2ex2+tx根的个数.

法一(全分离)

因x-e与lnx-lne同号,所以x≤e，

f(x)在(0,e)上单增,在(e,+∞)上单减.

且当x→0时,f(x)→-∞,当x→+∞时,f(x)→-∞.

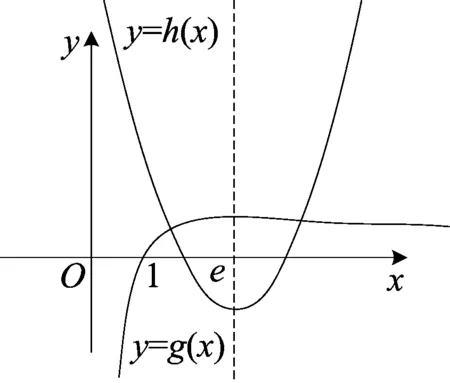
法二 (半分离)

易得g(x)在(0,e)上单增,在(e,+∞)上单减,且当x→0时,g(x)→-∞ ；

当x→+∞时,

又h(x)是二次函数,开口向上,对称轴为x=e,h(x)min=h(e)=t-e2.如图所示:

例7 已知a>0，函数f(x)=|x2+|x-a|-3|在区间[-1,1]上的最大值为2，则a=______.

解 (两重绝对值要脱去太难，因此转化为恒成立问题，再半分离)

即x∈[-1,1]时，|x2+|x-a|-3|≤2恒成立(等号要取)，

所以-2≤x2+|x-a|-3≤2⟹1-x2≤|x-a|≤5-x2.